动态规划-状态压缩dp

蒙德里安的梦想

问题描述

问题分析

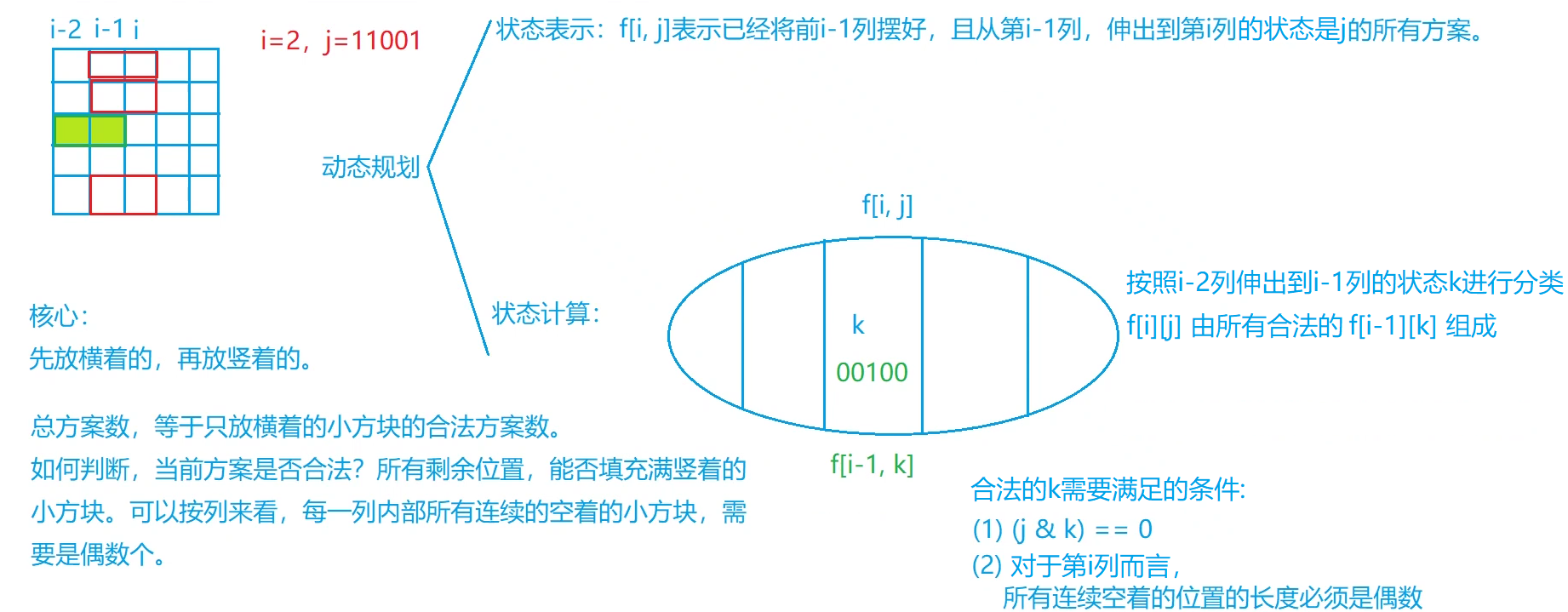
(f[i][j] = displaystyle sum_{0到1<<n - 1中所有合法的k}(f[i - 1][k]))
(f[m][0])的含义为前(m-1)列摆好，且从第(m-1)列伸出到第m列状态为(0)的方案数，显然这就是答案(原因见下图)

(k)是否合法需要看(k)和(j)的关系，第一个条件表示第(i-2)列伸出到第(i-1)列时就不能从第(i-1)列伸出到第(i)列，即第(i-1)列不能出现冲突
第2个条件表示我们在确定横着放的方格之后需要关注竖着放的方格是否能填满剩余空间，即连续的空的方格是否为偶数个(因为1*2的方格竖着放占用两个格)，摆完之后，第(i-1)列空着的方格已经固定了，我们需要判断的就是第(i-1)列中连续的空方格是否为偶数个，即判断 (j | k) 这个状态是否为合法状态。

代码实现

代码包含两次优化

/** 
 * 完全遵照原理的写法，但是在一组查询中由于check会进行重复判断所以会超时，于是考虑预处理
 * 预处理不能放在询问之前是因为预处理需要枚举所有状态，前提是已知行数才能确定所有状态，所以预处理需要在每一次询问时才能进行
 */
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 12, M = 1 << N; // 列需要从0到11

int n, m;
LL f[N][M];

bool check(int j, int k)
{
    if ((j & k) != 0) return false;
    
    int u = j | k, cnt = 0; // cnt 表示u中连续的0的数目
    for (int i = 0; i < n; ++ i)
    {
        if (u >> i & 1) // 遇到某位为1
        {
            if (cnt & 1) return false; // 当前这个1之前连续的0的数目为奇数
            cnt = 0;
        }
        else ++ cnt;
    }
    if (cnt & 1) return false; // 用来判断像01这种最后是0的情况
    return true;
}
int main()
{
    init();
    while (cin >> n >> m, n || m)
    {
        memset(f, 0, sizeof f);
        f[0][0] = 1; // 从第-1列伸出到第0列只有状态为0表示不伸出是有意义的且表示一种状态数值为1，其余状态不存在均为0
        for (int i = 1; i <= m; ++ i)
            for (int j = 0; j < 1 << n; ++ j) // 所有状态
                for (int k = 0; k < 1 << n; ++ k) // 所有状态
                    if (check(j, k))
                        f[i][j] += f[i - 1][k];
                        
        cout << f[m][0] << endl;
    }
    return 0;
}

/**
 * 预处理所有状态是否为合法状态
 */
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 12, M = 1 << N; // 列需要从0到11

int n, m;
LL f[N][M];
bool st[M]; // st[i]:状态i是否为合法状态

int main()
{
    while (cin >> n >> m, n || m)
    {
        // 预处理
        for (int i = 0; i < 1 << n; ++ i)
        {
            int cnt = 0;
            st[i] = true;
            for (int j = 0; j < n; ++ j)
                if (i >> j & 1)
                {
                    if (cnt & 1) 
                    {
                        st[i] = false;
                        break;
                    }
                    cnt = 0;
                }
                else ++ cnt;
            if (cnt & 1) st[i] = false;
        }
        
        memset(f, 0, sizeof f);
        f[0][0] = 1; // 从第-1列伸出到第0列只有状态为0表示不伸出是有意义的且表示一种状态数值为1，其余状态不存在均为0
        for (int i = 1; i <= m; ++ i)
            for (int j = 0; j < 1 << n; ++ j) // 所有状态
                for (int k = 0; k < 1 << n; ++ k) // 所有状态
                    if ((j & k) == 0 && st[j | k])
                        f[i][j] += f[i - 1][k];
                        
        cout << f[m][0] << endl;
    }
    return 0;
}
/**
 * 进一步优化：选定j时k的合法情况是固定的几种，在i次遍历中每次k都进行了一些无效遍历，
 * 优化方法为预处理出和j对应的所有合法情况
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 12, M = 1 << N; // 列需要从0到11

int n, m;
LL f[N][M];
bool st[M]; // st[i]:状态i是否为合法状态
vector<int> state[M]; // state[i]:与状态i对应的合法状态

int main()
{
    while (cin >> n >> m, n || m)
    {
        // 预处理出所有状态是否合法
        for (int i = 0; i < 1 << n; ++ i)
        {
            int cnt = 0;
            st[i] = true;
            for (int j = 0; j < n; ++ j)
                if (i >> j & 1)
                {
                    if (cnt & 1) 
                    {
                        st[i] = false;
                        break;
                    }
                    cnt = 0;
                }
                else ++ cnt;
            if (cnt & 1) st[i] = false;
        }
        
        // 预处理出和j对应的合法k
        for (int j = 0; j < 1 << n; ++ j)
        {
            state[j].clear();
            for (int k = 0; k < 1 << n; ++ k)
                if ((j & k) == 0 && st[j | k])
                    state[j].push_back(k);
        }
        
        memset(f, 0, sizeof f);
        f[0][0] = 1; // 从第-1列伸出到第0列只有状态为0表示不伸出是有意义的且表示一种状态数值为1，其余状态不存在均为0
        for (int i = 1; i <= m; ++ i)
            for (int j = 0; j < 1 << n; ++ j) // 所有状态
                for (int k : state[j])
                    f[i][j] += f[i - 1][k];
                        
        cout << f[m][0] << endl;
    }
    return 0;
}

最短Hamilton路径

问题描述

给定一张 n 个点的带权无向图，点从 0~n-1 标号，求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径(哈密顿路径)的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。

问题分析

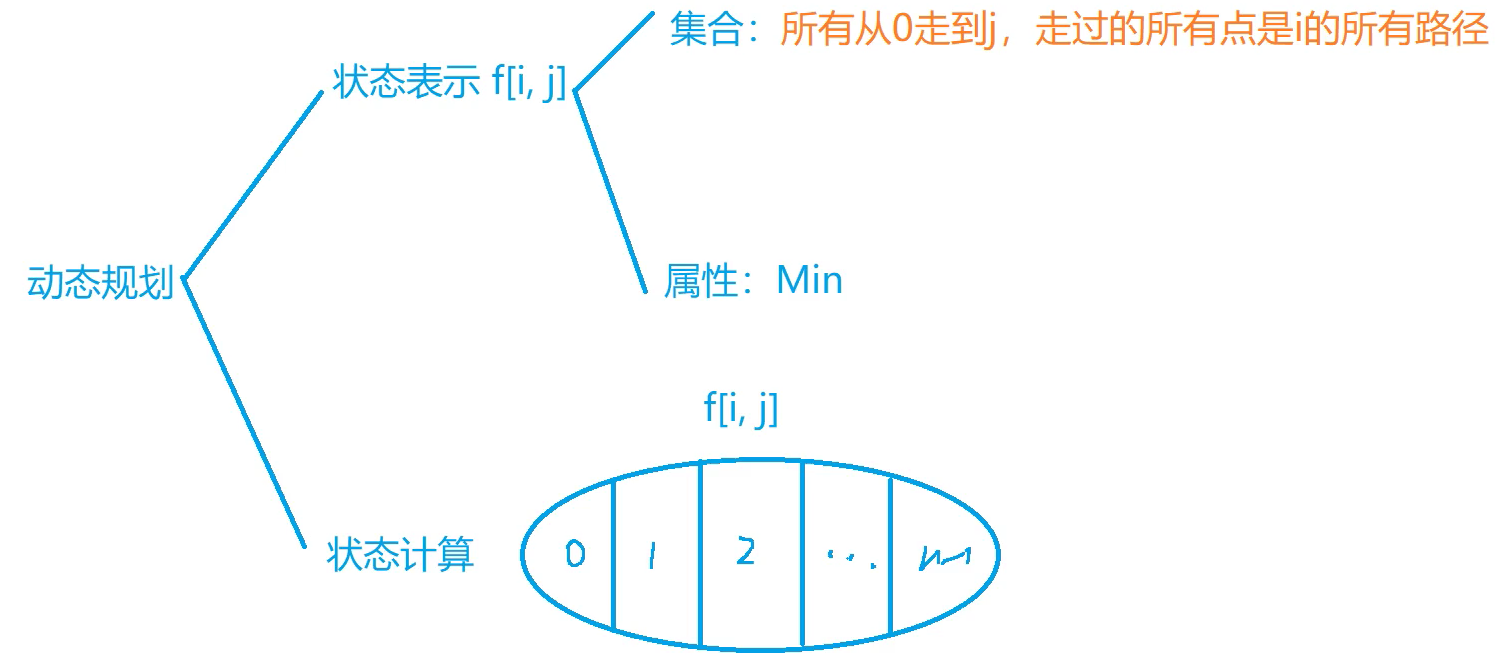
状态表示：(f[i][j]) 表示所有“经过的点集是(i)，最后位于点(j)的路线”的长度的最小值(i包含现在已经走过的所有点，包含j点)

状态计算一般对应集合划分。这里可以将(f[i][j])所表示的集合中的所有路线，按倒数第二个点分成若干类，其中第(k)类是指倒数第二个点是(k)的所有路线。从(0)走到(j)的最短路径等于从(0)走到(k)的最短路径+从(k)走到(j)的路径，从(0)走到(k)走过的点相较于从(0)走到(j)而言，少了(j)点，所以经过的点为(i)减去一个(j)点，即(f[i][j] = min(f[i - {j}][k] + w[k][j]))

代码实现

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 20, M = 1 << N;

int n;
int w[N][N];
int f[M][N]; // 注意第一维是状态，数量不再是N了

int main()
{
    cin >> n;
    for (int i = 0; i < n; ++ i)
        for (int j = 0; j < n; ++ j)
            cin >> w[i][j];
    
    // f[i][j]中i的范围从0到1<<n-1，0表示所有点都未选择，1<<n-1表示所有点都选择(其实就是一个n位的二进制数的最大值)
    memset(f, 0x3f, sizeof f); // 取最小值初始值要赋值为无穷大
    f[1][0] = 0; // f[0][] = INF,所有点都不选择，到达任意点的距离均为无穷大，f[1][]表示走了第1个点，只有到这个点的距离为0，到其它点的距离均为无穷大
    
    // 根据状态转移方程可知，计算大的状态之前需要用到小的状态，所以必须保证大的状态计算之前小的状态已经被更新过了，所以先枚举状态
    for (int i = 0; i < 1 << n; ++ i) // 遍历走过点的所有可能情况
        for (int j = 0; j < n; ++ j)
            if (i >> j & 1) // 如果i表示走过的点中就没有j点，那么就没有后续操作的必要了,假设j=0，右移0位&1恰好代表的是第一个点的状态
                for (int k = 0; k < n; ++ k) // 枚举倒数第二个点
                    if ((i >> k & 1) && k != j) // 原因同上，后面的条件保证倒数第二个点和最后一个点不相同，不加答案也是对的，原因在于k==j时候，那么i - (1 << j)中就不包含k了，那么f[i - (1 << j)][k]这个状态就是一个不合法状态，值是正无穷，对f[i][j]的值是没有影响的
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]); // i的状态中去掉j点是i - (1 << j)，不懂带入数据
    
    cout << f[(1 << n) - 1][n - 1] << endl;
                    
    return 0;
}