欧拉函数公式
(n=p_1^{k_1} * p_2^{k_2} * ... * p_n^{k_n})
(phi(n) = n * displaystyle prod_{i = 1}^{n}(1 - frac{1}{p_i}))
试除法求欧拉函数
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
while (n --)
{
int x;
cin >> x;
int res = x;
for (int i = 2; i <= x / i; ++ i)
if (x % i == 0)
{
res -= res / i;
while (x % i == 0) x /= i;
}
if (x > 1) res -= res / x;
cout << res << endl;
}
}
筛法求欧拉函数
在一些情况,需要求出1到n所有数的欧拉函数,如果对每个数都使用试除法求一遍太慢了。而筛法求欧拉函数就可以用于这类问题
算法原理
下面的代码是欧拉筛的代码,在欧拉筛质数的过程中,可以顺带着求出所有数的欧拉函数值
void get_divisors(int n)
{
for (int i = 2; i <= n; ++ i)
{
if (!st[i]) primes[cnt ++] = i;
for (int j = 0; primes[j] <= n / i; ++ j)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
- 如果判定某个数p为质数,则可直接得出其欧拉函数值为p-1
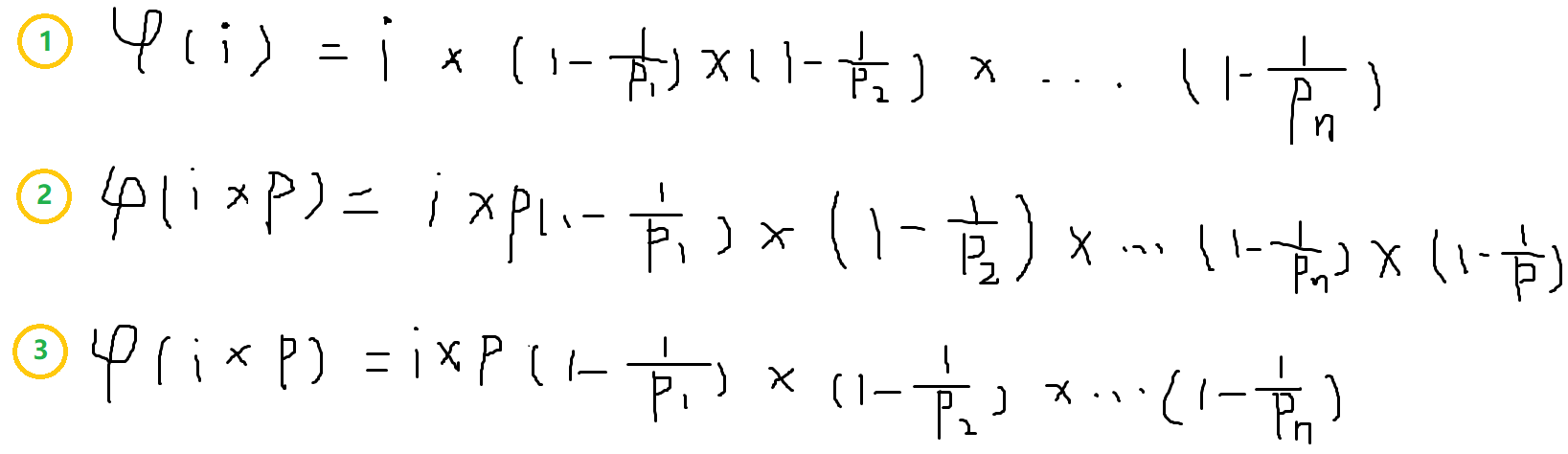
图中的p表示一个质数,和代码中的primes[j]是一样的
2. 如果 i % primes[j] == 0,说明primes[j]是i的最小质因子,即i的质因数中包含primes[j],所以primes[j]对于i的质因数分解的影响只是增加了其中某个质数的指数,并没有增加质因数的种类,所以对于计算欧拉函数的影响只不过是在i的欧拉函数值基础上乘以一个primes[j]即可(对应着3式)
3.如果i % primes[j] != 0,说明 primes[j]不是i的质因子,primes[j]对于i的质因数分解的影响是增加了一个质数,这是种类增多了,所以在计算欧拉函数时就需要多乘以一个(1-1/p)和primes[j],(对应着2式)
正确性说明
之前我们说明过枚举到i时,一定可以确定i是合数还是素数了,同理,也一定已经获得了i的欧拉函数值,所以才可以通过i和primes[j]的欧拉函数确定i * primes[j]的欧拉函数
代码实现
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int primes[N], cnt;
int phi[N];
bool st[N];
void get_divisors(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; ++ i)
{
if (!st[i])
{
phi[i] = i - 1;
primes[cnt ++] = i;
}
for (int j = 0; primes[j] <= n / i; ++ j)
{
st[i * primes[j]] = true;
if (i % primes[j] == 0)
{
phi[i * primes[j]] = phi[i] * primes[j]; // 对应3式
break;
}
phi[i * primes[j]] = phi[i] * (primes[j] - 1); // 对应2式,只不过把primes[j]*(1 - 1 / primes[j])乘进去了
}
}
}
int main()
{
int n;
cin >> n;
get_divisors(n);
long long res = 0;
for (int i = 1; i <= n; ++ i) res += phi[i];
cout << res << endl;
return 0;
}
欧拉函数的应用
欧拉定理
若n,a为正整数,且n,a互质,则: (a^{phi(n)} = 1 (mod n))
证明:1到n中与n互质的数设为 (x_1, x_2, ... x_{phi(n)})
所有项都乘以a(欧拉定理中与n互质的a),得到 (ax_1, ax_2, ... ax_{phi(n)})
如果满足 (ax_1 * ax_2 * ... * ax_{phi(n)} = x_1 * x_2 * ... * x_{phi(n)} (mod n))
即 (a^{phi(n)} * (x_1 * x_2 * ... * x_{phi(n)}) = x_1 * x_2 * ... * x_{phi(n)} (mod n))
因为 (x_1, x_2, ... x_{phi(n)}) 所有数都是与n互质的,所以他们的乘积 $ x_1 * x_2 * ... * x_{phi(n)} $ 也是与n互质的,所以根据某个定理 可以得到(a^{phi(n)} = 1 (mod n))
这里的某个定理还需要回学校看一下书,记不太清了
所以说我们的主要任务就是如何证明 (ax_1 * ax_2 * ... * ax_{phi(n)} = x_1 * x_2 * ... * x_{phi(n)} (mod n)) ,即证明 (ax_i) 和 (x_i)一一对应(顺序可能不同),因为 (ax_1, ax_2, ... ax_{phi(n)}) 是从 (x_1, x_2, ... x_{phi(n)}) 转变而来,所以一定是 (phi(n)) 项,但是乘以a之后可能有 (ax_i == ax_j),这样的话(ax_1, ax_2, ... ax_{phi(n)}) 中实质上就不是 (phi(n)) 项了,所以我们想要证明的自然是不成立的,但是假设存在 (ax_i = ax_j (mod n)) ,那么 (n | a(x_i - x_j)),因为n和a互质,所以 (n | x_i - x_j),但是所有的x都是比n小的数,这个结果显然是不成立的,所以我们的假设也不成立,所以证明了生成的数中两两modn不同余,所以也就证明了 (ax_i) 和 (x_i)一一对应,所以欧拉定理也就成立了
证明过程有些粗糙,可能存在问题,暂定这样写
求解最大公约数为某一特定值的数对个数
给定整数 (N),求 (0 ≤ x,y ≤ N) 且 (GCD(x,y)) 为1的数对 ((x,y)) 有多少对
算法原理
求解(gcd(x, y) = 1)的(x, y),这么看真的很难和欧拉函数建立起联系
但是当我加入(x > y)的条件时,这个问题就转变为了求比x小且与x互质的数的个数,此时很明显就是使用欧拉函数进行求解
同时可以发现当(x < y)时,答案数和(x > y)是一样的
最后特判(x = y)的情况即可
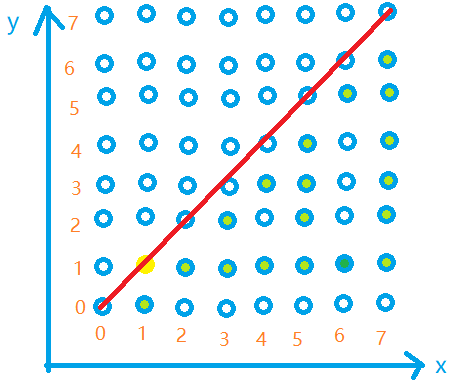
绿色点代表(x > y)时一些满足条件的数对,(x < y)的情况与其关于(y=x)的曲线对称
红色线表示(x = y)的直线
黄色点表示(x = y)时那一个满足条件的数对
流程
- 因为x会在区间内变化,所以每次求解需要多次查询,故先使用线性筛预处理所有可能数值的欧拉值
- 枚举x进行求解(范围参照上方图片进行推断)
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int phi[N];
int primes[N], cnt;
bool st[N];
void init(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; ++ i)
{
if (!st[i])
{
primes[cnt ++] = i;
phi[i] = i - 1;
}
for (int j = 0; primes[j] * i <= n; ++ j)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0)
{
phi[i * primes[j]] = phi[i] * primes[j];
break;
}
phi[i * primes[j]] = phi[i] * (primes[j] - 1);
}
}
}
int main()
{
init(N - 1);
int x;
cin >> x;
int res = 1;
for (int j = 1; j <= x; ++ j) res += phi[j] * 2;
cout << res << endl;
return 0;
}
问题推广
给定整数 (N),求 (1 ≤ x,y ≤ N) 且 (GCD(x,y)) 为p的数对 ((x,y)) 有多少对
算法原理
设(x' = frac{x}{p}, y' = frac{y}{p})
求解(gcd(x, y) = p)的数对((x,y))的个数可以等价为求解 (gcd(x', y') = 1) 的数对((x', y'))的个数
根据以下条件可推导出 (1 leq frac{x}{p}, frac{y}{p} leq frac{N}{p}), 即(1 leq x', y' leq frac{N}{p})
综上所述,目前的问题已经等价为
给定整数 (N),求 (1 ≤ x,y ≤ frac{N}{p}) 且 (GCD(x,y)) 为1的数对 ((x,y)) 有多少对
按照原问题的解法做即可