Unity 3-13 编程内功修炼 -- 算法
任务1&2:课程介绍
主要算法:
分治法
堆排序
二叉树
动态规划
贪心算法
图
任务3:分治算法 -- Divide and Conquer
分治算法:对于一个规模为n的问题,若该问题可以容易地解决(n较小),则直接解决
否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同
递归地解决这些子问题,然后将各子问题的解合并得到原问题的解。
使用分治法求解的一些经典问题:
二分搜索
大整数乘法
Strassen矩阵乘法
棋盘覆盖
合并排序
快速排序
线性时间选择
最接近点对问题
循环赛日程表
汉诺塔
任务4:最大子数组问题
&5:暴力求解最大子数组问题
&6&7:分治法求解最大子数组问题
最大子数组问题:

已知17天的股票价格, 问哪一天买入哪一天卖出收益最高
--> 问题转化:价格波动的哪一个子数组为最大子数组
任务5:暴力求解:
// Siki老师的方法 int[] priceArray = { 100, 113, 110, 85, 105, 102, 86, 63, 81,
101, 94, 106, 101, 79, 94, 90, 97 }; int[] priceFluctuationArray = new int[priceArray.Length - 1];//价格波动的数组 for (int i = 1; i < priceArray.Length; i++) { priceFluctuationArray[i - 1] = priceArray[i] - priceArray[i - 1]; } int total = priceFluctuationArray[0];//默认数组的第一个元素 是最大子数组 int startIndex = 0; int endIndex = 0; for (int i = 0; i < priceFluctuationArray.Length; i++) { //取得以i为子数组起点的 所有子数组 for (int j = i; j < priceFluctuationArray.Length; j++) { //由i j 就确定了一个子数组 int totalTemp = 0;//临时 最大子数组的和 for (int index = i; index < j + 1; index++) { totalTemp += priceFluctuationArray[index]; } if (totalTemp > total) { total = totalTemp; startIndex = i; endIndex = j; } } } Console.WriteLine("startindex : " + startIndex); Console.WriteLine("endIndex : " + endIndex); Console.WriteLine("购买日期是第"+startIndex+"天, 出售是第"+(endIndex+1)+"天"
+ ";盈利:" + total); Console.ReadKey();
我自己的改良方法:O(n^2)
// 已知股票的价格数组 int[] priceArray = { 100, 113, 110, 85, 105, 102, 86, 63, 81, 101, 94, 106, 101, 79, 94, 90, 97 }; // 求价格波动的数组 int[] priceFluctuationArray = new int[priceArray.Length-1]; for (int i = 1; i < priceArray.Length; i++) { priceFluctuationArray[i - 1] = priceArray[i] - priceArray[i - 1]; } // 计算每个子数组的值 // 从i到j的子数组 int maxInterest = priceFluctuationArray[0]; int startDate = 0; int endDate = 0; for (int i = 0; i < priceFluctuationArray.Length; i++) { int interest = 0; // 子数组头 for (int j = i; j < priceFluctuationArray.Length; j++) { // 子数组尾 interest += priceFluctuationArray[j]; if(interest > maxInterest) { startDate = i; endDate = j; maxInterest = interest; } } } Console.WriteLine("From " + startDate + " to " + (endDate+1) + "; interest: " + maxInterest); Console.ReadKey();
任务6:分治法求解

策略:
1. 设low为数组开始的index,high为数组结束的index
[low, high]
2. 取mid的index
[low, mid] [mid+1, high]
设i, j分别为最大子数组的开始索引和结束索引
三种情况:
a) i, j同时位于低区间
b) i, j同时位于高区间
c) i位于低区间,j位于高区间
分别求出这三种情况的最大子数组;比较这三个最大子数组,求出最大子数组
a和b情况均为将大数组变为小数组,可以使用递归来解决(分解为最小)
c情况很容易做到:分别取得i~mid的最大值,j~mid的最大值即可:O(n)
3. 重复步骤2(递归)
代码实现:
1. Main
求完priceFluctuationArray后
GetMaxSubArray(0, priceFluctuationArray.Length-1, priceFluctuationArray);
来得到最大子数组
2. 定义GetMaxSubArray();
返回值需要最大子数组的startIndex、endIndex和price的总和
因此设返回值为一个struct
Struct SubArray {
int startIndex; int endIndex; int total;
}
3. 定义GetMaxSubArray()为:
static SubArray GetMaxSubArray(int low, int high, int[] array);
4. 得到mid的值
int mid = (low + high) / 2;
5. 三种情况分别讨论
a) i, j 在低区间
GetMaxSubArray(low, mid, array);
// 需要保存返回值,因为最后要比较三种情况,得出最大子数组
SubArray subArray1 = GetMaxSubArray(...);
b) i, j 在高区间
SubArray subArray2 = GetMaxSubArray(mid+1, high, array);
c) i 在低区间,j 在高区间
// 不需调用,可以直接解决 -- 一个for循环
// i 在低区间 [low, mid] 找到最大子数组 [i, mid]
int maxLowTotal = array[mid];
int lowTotal = array[mid];
int startIndex = mid;
for (int i = mid-1; i >= low; i--) {
lowTotal += array[i];
if (lowTotal > maxLowTotal) {
maxLowTotal = lowTotal;
startIndex = i;
}}
// j 在高区间 [mid+1, high] 找到最大子数组 [mid+1, j]
for (int j = mid+1; j<= high; j++) {
highTotal += array[j];
if (highTotal > maxHighTotal) {
maxHighTotal = highTotal;
endIndex = j;
}}
// 得到该情况下的最大子数组
SubArray subArray3;
subArray.startIndex = startIndex;
subArray.endIndex = endIndex;
subArray.total = maxLowTotal + maxHighTotal;
6. 比较这三种情况下哪一个最大子数组会成为最终的最大子数组
if (subArray1.total >= subArray2.total && subArray1.total >= subArray3.total) {
return subArray1;
} else if (subArray2.total >= subArray1.total && subArray2.total >= subArray3.total) {
return subArray2;
} else {
return subArray3;
}
7. 那么,递归什么时候是个头呢?
当小数组只有一个元素的时候,即low=high的时候
此时,这个小数组的最大子数组就是本身
if(low == high) {
SubArray subArray = new SubArray();
subArray.startIndex = low;
subArray.endIndex = high;
subArray.total = array[low];
return subArray;
}
namespace 最大子数组问题___分治法 { class Program { //最大子数组的结构体 struct SubArray { public int startIndex; public int endIndex; public int total; } static void Main(string[] args) { int[] priceArray = { 100, 113, 110, 85, 105, 102, 86, 63,
81, 101, 94, 106, 101, 79, 94, 90, 97 }; int[] priceFluctuationf = new int[priceArray.Length - 1]; for (int i = 1; i < priceArray.Length; i++) { priceFluctuationf[i - 1] = priceArray[i] - priceArray[i-1]; } SubArray subArray = GetMaxSubArray(0, priceFluctuationf.Length-1, priceFluctuationf); Console.WriteLine(subArray.startIndex); Console.WriteLine(subArray.endIndex); Console.WriteLine("我们在第" + subArray.startIndex + "天买入,在第" + (subArray.endIndex + 1) + "天卖出"); Console.ReadKey(); } // 这个方法是用来取得array 这个数组 从low到high之间的最大子数组 static SubArray GetMaxSubArray(int low, int high, int[] array) { if (low == high) { // 分治到最小部分 SubArray subArray; subArray.startIndex = low; subArray.endIndex = high; subArray.total = array[low]; return subArray; } else { // 三种情况 // a) i, j同时位于低区间 // b) i, j同时位于高区间 // c) i位于低区间,j位于高区间 int mid = (low + high) / 2; // a) SubArray subArray1 = GetMaxSubArray(low, mid, array); // b SubArray subArray2 = GetMaxSubArray(mid + 1, high, array); // c // i 在低区间 [low, mid] 找到最大子数组 [i, mid] int maxLowTotal = array[mid]; int lowTotal = array[mid]; int startIndex = mid; for (int i = mid - 1; i >= low; i--) { lowTotal += array[i]; if (lowTotal > maxLowTotal) { maxLowTotal = lowTotal; startIndex = i; } } // j 在高区间 [mid+1, high] 找到最大子数组 [mid+1, j] int maxHighTotal = array[mid + 1]; int highTotal = array[mid + 1]; int endIndex = mid + 1; for (int j = mid + 2; j <= high; j++) { highTotal += array[j]; if (highTotal > maxHighTotal) { maxHighTotal = highTotal; endIndex = j; } } SubArray subArray3; subArray3.startIndex = startIndex; subArray3.endIndex = endIndex; subArray3.total = maxLowTotal + maxHighTotal; // 比较这三种情况下哪一个最大子数组会成为最终的最大子数组 if (subArray1.total >= subArray2.total && subArray1.total >= subArray3.total) { return subArray1; } else if (subArray2.total >= subArray1.total && subArray2.total >= subArray3.total) { return subArray2; } else { return subArray3; } } } } }
任务8:树(数据结构)
树 (Tree)是n(n>=0)个结点的有限集。
n=0时称为空树
在任意一棵非空树中,1. 有且仅有一个特定的结点称为根结点 (root)
2. 当n>1时,其余结点可分为m(m>0)个互不相交的有限集,其中每个集合本身又是一棵树
并称为根的子树 (SubTree)
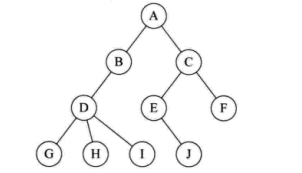
一些概念:
结点的度:拥有子树的个数
树的层次:根结点为第一层,根结点的子结点为第二层,以此类推
树的深度:最大的层次
兄弟关系:有同一个父亲结点的两个子结点之间的关系为兄弟关系(如G和H)
堂兄弟关系:层次相同(没有共同父亲的即为堂兄弟,如I和J)
一个结点只能有一个父结点,子树之间是不相交的
任务9:树的存储结构
存储结构:顺序存储和链式存储
如果使用顺序存储(数组),结点之间的关系就很难表示出来
因此使用链式存储:
1. 双亲表示法 -- ![]()
优点:可以很方便地访问父亲结点
缺点:不容易访问兄弟结点和子结点
2. 孩子表示法 -- ![]()
优点:通过父亲能很方便地访问所有子结点
缺点:不容易访问父亲结点和兄弟结点;
浪费空间:每个结点的孩子数量不同,有很多指向孩子地址的空间为null
3.孩子兄弟表示法 -- ![]()
保存了第一个孩子和右边的兄弟
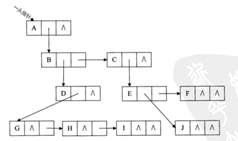
优点:方便地访问所有的子结点(通过firstchild访问rightsib即可)
方便地访问它的兄弟
缺点:不容易访问父结点
4. 还有其他表示法
任务10&11:二叉树的定义和性质(满二叉树、完全二叉树)
二叉树 (Binary Tree):每个结点最多有两个子结点(子结点有左右的顺序)
左右子树:每个结点可能有一个左子树和/或一个右子树
特殊二叉树:
斜树:(左斜树、右斜树):所有结点只有左 (右)子树的二叉树
满二叉树:树的任意一个结点都有两个子结点(叶子结点没有子结点)
完全二叉树:对一棵具有n个结点的二叉树按层序编号,如果编号为i (1<=i<=n)的结点与同
样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则该树为完全二叉树
(树的任意一个结点都有两个子结点(最后一层叶子结点可以从右开始连续缺失))
满二叉树一定是完全二叉树,反之就不对了
二叉树的性质:
二叉树的第i层上最多有2(i-1)个结点
深度为k的二叉树至多有2k-1个结点
20+21+22+23+24+...+2k-1
= 20+21+22+23+24+...+2k-1 + 1 - 1
= 1 + 20+21+22+23+24+...+2k-1 - 1
= 20 + 20+21+22+23+24+...+2k-1 - 1
= 2k - 1
n个结点的完全二叉树,对结点从1开始编号(按满二叉树的方式),对任意结点i有:
a) 它的父结点是 i/2
b) 它的左孩子是 2i, 右孩子是2i+1
c) 如果2i>n 说明无子结点;如果2i+1>n说明无右孩子
任务12:二叉树的存储结构
对于一般树来说,使用链式存储比较方便。
但是对于二叉树来说,兄弟、父亲、孩子可以很方便的通过编号得到,所以使用顺序存储
顺序存储:将所有二叉树都当作完全二叉树来存储
依次按结点编号(从1开始)放入数组(编号=index+1)
不存在的结点=null即可 -- 非完全二叉树会有空间浪费
链式存储:结点结构:![]()
无法方便地访问父结点;一个结点需要三倍内存空间;
头结点head指向根结点;每个结点的两个指针指向存在的子结点
任务13:二叉树的四种遍历方法
二叉树的遍历是指:从根结点出发,按照某种次序依次访问二叉树中的所有结点,使每个结点仅被访问一次
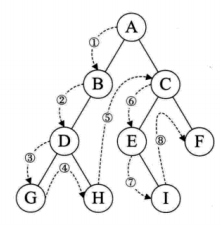
前序遍历:先输出当前结点的数据,再依次遍历输出左结点和右结点
ABDGHCEIF
中序遍历:先遍历输出左结点,再输出当前结点的数据,再遍历输出右结点
GDHBAEICF
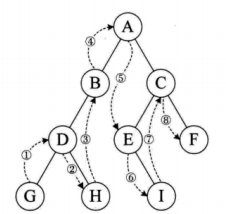
后序遍历:先遍历输出左结点,再遍历输出右结点,最后输出当前结点的数据
GHDBIEFCA

层序遍历:从树的第一层开始,从上到下逐层遍历;同一层中,从左到右对结点逐个访问输出
ABCDEFGHI

任务14&15&16:代码实现二叉树的顺序存储和遍历
使用数组实现二叉树
class BiTree<T> { private T[] data; private int count = 0; public BiTree(int capacity) { data = new T[capacity]; } public bool Add(T item) { if (count >= data.Length) { // 二叉树满了 return false; } data[count] = item; count++; return true; } ... }
二叉树的遍历:
前序遍历:void FirstTraversal(int index) {
// index为想要遍历的索引
// 先输出结点数据
Console.Write(data[index]);
// 得到要遍历的结点编号
int number = index + 1;
// 遍历左子结点
FirstTraversal(number * 2 - 1); // index = number - 1
// 遍历右子结点
FirstTraversal(number * 2 + 1 - 1);
}
但是,每一种递归都需要一个终止条件,当结点没有子结点的时候,即可返回
if(index >= data.Length) return;
而且,当二叉树不是完全二叉树时,需要判断结点是否为空
if(data[index] == null) return;
如何开始遍历呢?遍历编号为1的结点即可;
外界调用封装好的方法 public void FirstTraversal();
public void FirstTraversal() {
FirstTraversal(0);
}
并设FirstTraversal(int index) 为 private
// siki老师的方法 public void FirstTraversal() { FirstTraversal(0); } private void FirstTraversal(int index) { if (index >= count) return; //得到要遍历的这个结点的编号 int number = index + 1; if (data[index].Equals(-1)) return; Console.Write(data[index] + " "); //得到左子结点的编号 int leftNumber = number * 2; int rightNumber = number * 2 + 1; FirstTraversal(leftNumber - 1); FirstTraversal(rightNumber - 1); }
// 我的方法 public void FirstTraversal() { FirstTraversal(0); } private void FirstTraversal(int index) { // index为想要遍历的索引 // 先输出结点数据 if(data[index ] == null) { return; } Console.Write(data[index]); // 得到要遍历的结点编号 int number = index + 1; if (number*2<=count) { // 遍历左子结点 FirstTraversal(number * 2 - 1); } if(number * 2 + 1 <= count) { // 遍历右子结点 FirstTraversal(number * 2 + 1 - 1); } }
中序遍历:
后序遍历:
层序遍历:
任务17:二叉排序树/ 二叉查找树
二叉排序树:对于任意结点,若左子树不为空,则左子树上所有结点的值均小于根结点的值
若右子树不为空,则右子树上所有结点的值均大于根结点的值
优点:排序方便(直接通过中序遍历就能得到有序结果),
查找方便(从根结点开始,判断往左/ 右子树继续查找即可)
插入方便(与查找相似)
二叉排序树的删除操作:
1. 删除叶子结点:直接删除
2. 删除的结点只有一个子结点(左图):用子结点替换掉被删除的结点
删除的结点只有一个子树(右图):用子树的根结点替换掉被删除的结点
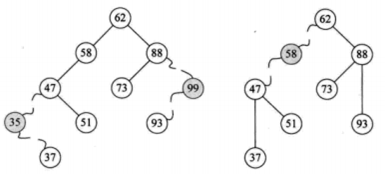
37替代35,93替代99 47替代58,直接建立47~62的连接
3. 删除的结点有两个子结点/子树:
需要选出所有子结点中间大小的结点
a) 找到左子树中的最右子结点(for遍历所有的右结点)(左子树中的最大值)
b) 找到右子树中的最左子结点(for遍历所有的左结点)(右子树中的最小值)
链式结构:由于二叉树的结点的位置由自身值的大小有关系,因此需要使用链式结构存储
任务18&19&20&21:二叉排序树的代码实现
添加操作
。。。
排序和查找
。。。
查找方法的优化
。。。
删除操作
。。。
任务22:堆和堆排序
堆:完全二叉树
大顶堆:每个结点的值都大于或等于其孩子结点的值
小顶堆:每个结点的值都小于或等于其孩子结点的值
堆排序:利用堆来进行排序
将待排序的序列构造成一个大顶堆,此时整个序列的最大值就是根结点。
将它和堆的最后一个元素交换,此时末尾元素就是最大值
将剩余的n-1个序列重新构造成一个堆,这样就会得到n各元素中的次小值
反复执行就能得到一个有序序列
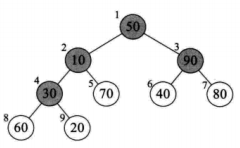
思路:
使用顺序结构存储完全二叉树
构造大顶堆:
叶子结点本身是一个大顶堆,无序遍历
将[30, 60, 20]构造成一个大顶堆 --> 取最大值60,与根结点30交换即可
将[10, 60, 70]构造成一个大顶堆 --> 取最大值70,与根结点10交换即可
但是交换之后,编号为4的结点发生了变化,需要遍历以下整棵子树构造大顶堆
任务23:大顶堆的代码实现
。。。
任务24:堆排序的代码实现
。。。
。。。
任务25:动态规划算法 (Dynamic Programming)
动态规划算法:基于一个递归公司及一个或多个初始状态。
当前子问题的解由上一次子问题的解推出。
动态规划和分治法相似,都是通过组合子问题的解来求解原问题。
分治法:问题划分成互不相交的子问题,递归求解子问题,再将子问题的解组合
动态规划:子问题重叠(不同子问题具有公共的子子问题)。
此时分治法会反复求解那些公共子问题 (没必要)
而动态规划算法对每个子子问题求解一次,并将结果保存,无需重新计算
动态规划的方法进行求解:
动态规划算法安排求解的顺序,对每个子问题只求解一次,并将结果保存下来。
如果随后再次需要此子问题的解,只需查找保存的结果,不必重新计算。
因此动态规划的方法是付出额外的内存空间,来节省计算时间。
动态规划的两种实现方法:
方法一:带备忘的自顶向下法
按照自然的递归形式编写过程,但过程中会保存每个子问题的解(通常保存在一个数组中)。
当需要计算一个子问题的解时,过程首先检查是否已经保存过此解。
如果是,则直接返回保存的值,从而节省了计算时间;
如果没有保存过此解,按照正常方式计算这个子问题。
方法二:自底向上法
首先恰当的定义子问题的规模,使得任何问题的求解都只依赖于更小的子问题的解。
因而我们将子问题按照规模排序,按从小到大的顺序求解。
当求解某个问题的时候,它所依赖的更小的子问题都已经求解完毕,结果已经保存。
两个实例讲解动态规划算法:
钢条切割问题(见任务26)
背包问题(见任务31)
任务26&27:钢条切割问题分析(动态规划)
已知出售一段长度为i英寸的钢条的价格为pi (i=1,2,3...)。
给一段长度为n的钢条,问怎么切割收益rn最大
![]()
比如:
n=1: 长度为1,价格为1
n=2: 长度为2,价格为5;
长度为1+1,价格为1+1=2;
n=3: 长度为3,价格为8;
长度为1+2,价格为1+5=6;
长度为1+1+1,价格为1+1+1=3;
n=4: 长度为4,价格为9;
长度为1+3,价格为1+8=9;
长度为1+1+2,价格为1+1+5=7;
长度为1+1+1+1,价格为1+1+1+1=4;
长度为1+2+1,价格为1+5+1=7;
长度为2+2,价格为5+5=10;
长度为2+1+1,价格为5+1+1=7;
长度为3+1,价格为8+1=9;
假设最优解把n段切割成了k段:n = i1 + i2 + i3 + ... + ik (1<=k<=n)
最大收益rn = pi1 + pi2 + pi3 + ... + pik
求解方案:
第一种方案:(递归求解,递归太多,过于复杂)
1. 不切割:收益为pn
2. 切割成两半:分解为两个子问题
rn = max(pn, (r1 + rn-1), (r2 + rn-2), ... , (rn-1 + r1))
第二种方案:
从钢条的左边切下长度为i (i=n即不切割(i!=0))的一段,
只对右边剩下长度为n-i的一段继续切割
rn = max((p1 + rn-1), (p2 + rn-2), ... , (pn-1 + r1), (pn + 0))
与第一种方案的区别:
每次递归调用的时候只需递归一种情况而不是两种情况
代码实现:自顶向下递归实现(求rn需要求rn-1,求rn-1需要求rn-2,最后需要求r1)
任务28&29&30:钢条切割问题的三种代码实现
。。。
。。。
。。。
任务31:0-1背包问题简介
&33:背包问题的动态规划分析
有容量m kg的背包,另外有i种 (1~i)物品 (每种只有一个),总量分别为w[1] w[2] ... w[i] (kg)
价值分别为p[1] p[2] ... p[i] (元)
问将哪些物品放入背包可以使得背包的总价值最大?最大价值是多少?
穷举法:把所有情况列出来,比较得到总价值最大的情况(O(2n))
动态规划:i个物品放入容量为m(kg)的背包的最大价值 (记为c[i, m])
对于每种物品只有两种选择:装入 或 不装入 -- 01背包问题
每种物品不能装入多次
对于c[i. m]有几种情况:
c[i, 0] = c[0, m] = 0;
c[i, m] = c[i-1, m] (w[i]>m)
当w[i]<=m时,两种情况:
不放入i,c[i, m] = c[i-1, m]
放入i,c[i, m] = c[i-1, m-w[i]] + p(i)
--> c[i, m] = max(放入i, 不放入i)
将c[i, m]的问题分解为小问题,直到c[0, m]或c[i, 0]返回 -- 递归 -- 自顶向下
大问题依赖着小问题,从小问题向上解决到大问题也可以完成 -- 自底向上
任务32:使用穷举法实现背包问题
。。。
任务34&35&36:三种方式实现背包问题(代码)
(不带备忘的自顶向下法/ 带备忘的自顶向下法/ 自底向上法)
。。。
。。。
。。。
任务37:贪心算法
对于许多最优化问题 (钢条切割问题--最大收益/ 背包问题--最大价值),使用动态规划算法有些没必要
可以使用更加简单高效的算法 -- 贪心算法
贪心算法在每一步做出当时看起来最佳的选择,即从每一次局部最优的选择,得到最后全局最优解
对于某些问题并不能保证得到最优解,但对很多问题确实可以得到最优解。
但即使某些时候不能得到最优解(而是次优解),我们也可能会选择贪心算法求解 -- 高效
任务38:活动选择问题(贪心算法)
有n个需要在同一天使用同一个教室的活动a1, a2, ..., an,教师同一时刻只能由一个活动使用。
每个活动ai都有一个开始时间si和结束事件fi;一旦被选择后,活动ai就占据时间区间 [si, fi)
如果 [si, fi) 和 [sj, fj) 互不重叠,ai和aj两个活动就可以被安排在这一天。
活动选择问题:安排这些活动,使尽量多的活动能不冲突地在这一天举行 (最大兼容活动子集)
注:是尽量多的活动,而不是尽可能长的时间
最大兼容子集可能不是唯一的。
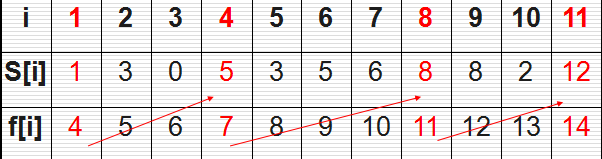
如:{a1, a4, a8, a11} 和 {a2, a4, a9, a11} 都是最大兼容子集
任务39&40&41:动态规划思路解决活动选择问题
。。。
。。。
。。。
任务42&43&44:贪心算法解决活动选择问题

什么是局部最优选择:
对于任何非空集合S,若am是S中结束时间最早的活动,则am一定在S的某个最大兼容子集中
证明 -- 反证法:
反证:am不在任意一个S的最大兼容子集中
证明1号活动不在最大兼容子集中
如果1号活动在最大兼容子集中,则最大兼容子集为1号活动 + [4, 24)中的最大兼容子集
如果1号活动不在最大兼容子集中,则后面肯定有一个活动是在最大兼容子集中的
假如是3号,则最大兼容子集为3号活动 + [6, 24)中的最大兼容子集
而[4, 24)肯定比[6, 24)的时间长,因此a3开始的兼容子集肯定不会比a1开始的大
那么如果3号开始的兼容子集最大,那么1号开始的也肯定是最大兼容子集 (数量相等)
因此1号活动肯定在最大兼容子集中
因此a1一定在S的某个最大兼容子集中。
无法一步到位直接找到最大兼容子集的话,寻找局部最优选择(找到头活动--结束时间最早)
1. 将所有活动按照结束时间早晚进行排序
2. 判断开始时间是否满足条件 + 比较结束时间是否最早 (无需判断,因为已经有序):遍历即可
在(0-24)这段时间中,1号活动一定在最大兼容子集中(结束时间最早)
剩下(4~24)这段时间,寻找4点以后开始,结束时间最早的活动 -- 子问题
。。。
。。。
。。。
任务45:钱币找零问题(贪心算法)
假设1元、2元、5元、10元、20元、50元和100元纸币分别有c0, c1, ... c6张来支付K元,至少要几张
贪心算法:每一步尽可能用面值大的纸币
static void Main(string[] args) { int[] count = { 3, 0, 2, 1, 0, 3, 5 }; int[] amount = { 1, 2, 5, 10, 20, 50, 100 }; int[] result = Change(324, count, amount); foreach (int i in result) { Console.Write(i + " "); } Console.ReadKey(); } public static int[] Change(int k, int[] count, int[] amount) { int[] result = new int[count.Length + 1]; // 最后一位表示未支付金额 // 当k的金额比所有纸币的总额都大,无法达到要求 // 当小面额的纸币不够补足k的零头,无法达到要求,比如本例中k=4时 for (int i = count.Length - 1; i >= 0; i--) { if(k<=0) { break; } // 情况1:k比该面额大 // 情况2:k比该面额小 if (count[i] >= k / amount[i]) { result[i] = k / amount[i]; k %= amount[i]; } else { // 情况3:该面额数量太少,没有足够该面额纸币 result[i] = count[i]; k -= (count[i] * amount[i]); } } result[result.Length - 1] = k; // 最后一位存储未支付金额 return result; }
任务46:图
图的主要应用是在地图上,如导航寻路等;
如地图上有一个物品,需要自动寻路捡起该物品 -- 求最短路径
图 Graph:由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为 G<V,E> (Vertex, Edge)
注:图的顶点不能是空的,但是边可以为空
顶点之间的关系:多对多
图的有关定义:
无向边:顶点之间的边没有方向,用无序偶对(vivj)表示
无向图 (Undirected graph):图中任意两个顶点之间的边都是无向边
有向边/ 弧 (Arc):用有序偶对<vi, vj>表示从vi到vi的有向边,vi为弧尾(Tail),vj为弧头(Head)
简单图:不存在顶点到自身的边,且同一条边不重复出现
连通图 (Connected graph):
图的存储:
邻接矩阵 Adjacency Matrix(两个数组,一维数组存储顶点信息,二维数组存储边或弧的信息)
邻接表 Adjacency List(数组与链表相结合,一维数组存储顶点和指向第一个邻接点的指针,
便于查找该顶点的边信息,每个顶点vi的所有邻接点构成一个线性表(单链表))
十字链表 Orthogonal List:把邻接表和逆邻接表结合起来
(邻接表关心了出度问题,逆邻接表关心了入度问题)
邻接多重表......
边集数组......
图的遍历:
深度优先 Depth First Search (DFS):类似于树的前序遍历
从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发,深度优先遍历图,
直到图中所有和v有路径相通的顶点都被访问到
对于非连通图:若图中还有顶点未被访问,则另选图中一个未曾访问的顶点开始DFS
广度优先 Breadth First Search (BFS):类似于树的层序遍历
最小生成树 Minimum Cost Spanning Tree:构造连通网的最小代价生成树
Prim算法:
Kruskal算法:
最短路径:
Dijkstra算法:按路径长度递增的次序 O(n2)
一步步求出它们之间顶点的最短路径,过程中都是基于已经求出的最短路径的基础上求得
更远顶点的最短路径
注:要求图中不存在负权边
Floyd算法:
拓扑排序:
关键路径: