旅行传送门
A - Exact Price
AC代码:
#include <bits/stdc++.h>
int main()
{
int n;
scanf("%d", &n);
puts((n && (n % 100 == 0)) ? "Yes" : "No");
return 0;
}
B - String Shifting
题意:给你一个字符串 \(S\) ,你可以进行下列操作之一任意次:
- 将第一个字符移至字符串末尾
- 将最后一个字符移至字符串开头
求可以得到的字典序最小与最大的字符串。
题目分析:字典序最小显然是以字符串中最小的字符开头,因此我们可以用一个数组 \(pos\) 存下字符串中最小字符出现的位置然后遍历,交换 \(S\) 中 \(1\) ~ \(pos_{i-1}\) 和 \(pos_i\) ~ \(len\) 这两段后更新答案即可,反之亦然。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
#define pdd pair<double, double>
#define IOS \
ios::sync_with_stdio(false); \
cin.tie(nullptr); \
cout.tie(nullptr);
using namespace std;
int main(int argc, char const *argv[])
{
string s;
cin >> s;
vector<int> pos[100];
rep(i, 0, s.length()) pos[s[i] - 'a'].push_back(i);
int mn, mx;
rep(i, 0, 25)
{
if (pos[i].size())
{
mn = i;
break;
}
}
down(i, 25, 0)
{
if (pos[i].size())
{
mx = i;
break;
}
}
string ans = s;
for (auto idx : pos[mn])
{
string t1 = s.substr(0, idx);
string t2 = s.substr(idx, s.length() - idx);
ans = std::min(ans, t2 + t1);
}
cout << ans << endl;
ans = s;
for (auto idx : pos[mx])
{
string t1 = s.substr(0, idx);
string t2 = s.substr(idx, s.length() - idx);
ans = std::max(ans, t2 + t1);
}
cout << ans << endl;
return 0;
}
C - Doukasen
题意:有一串保险丝,每根保险丝的长度和燃烧速度不同,现同时从左右端点燃,问火苗相遇时的位置与最左端的距离。
题目分析:双指针模拟。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
#define pdd pair<double, double>
#define IOS \
ios::sync_with_stdio(false); \
cin.tie(nullptr); \
cout.tie(nullptr);
using db = double;
using namespace std;
int main(int argc, char const *argv[])
{
IOS;
int n;
cin >> n;
std::vector<pdd> a(n + 1);
rep(i, 1, n) cin >> a[i].first >> a[i].second;
db ans = 0;
int l = 1, r = n;
while (l < r)
{
db t1 = a[l].first / a[l].second;
db t2 = a[r].first / a[r].second;
if (t1 < t2)
{
ans += a[l].first;
a[r].first -= t1 * a[r].second;
++l;
}
else if (t1 > t2)
{
ans += t2 * a[l].second;
a[l].first -= t2 * a[l].second;
--r;
}
else
{
ans += a[l].first;
++l, --r;
}
}
if (l == r)
ans += a[l].first / 2;
cout << fixed << setprecision(15) << ans << endl;
return 0;
}
D - Restricted Permutation
题意:给你两个序列 \(A\) 与 \(B\) ,要你构造出满足下列条件的序列 \(P\) :
- 对每个下标 \(i\) , \(A_i\) 在 \(P\) 中的位置比 \(B_i\) 靠前
- 字典序最小
题目分析:首先考虑什么时候不存在这样的序列 \(P\) ?不难发现,\(AB\) 中元素的出现顺序是具有“传递性”的,举栗子的话就是,假设有 \(i,j \in (\mathcal{1,2…n})\) ,存在 \(A_i = a , A_j = b\) 与 \(B_i = b , B_j = c\) ,即存在 \(a < b\) 与 \(b < c\) (这里的 \(<\) 代表出现位置更靠前),因此可得 \(a < c\) ,所以若是传递过程中出现矛盾(既有 \(a < c\) 又有 \(c < a\) )则序列不存在。
那如何判断有没有矛盾呢?对每组 \(\{A_i,B_i\} = \{x,y\}\) ,我们不妨由 \(x\) 向 \(y\) 连一条有向边,代表 \(x < y\) ,最好连出来的图中如果存在环,说明存在矛盾。那怎么去环呢?拓扑排序,至此整个题目的解法也就水落石出了,字典序最小只需用优先队列维护即可。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
const int maxn = 2e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int n, m;
int in[maxn];
std::vector<int> ans, e[maxn];
std::priority_queue<int, std::vector<int>, std::greater<int>> q;
int main(int argc, char const *argv[])
{
n = read(), m = read();
rep(i, 1, m)
{
int u = read(), v = read();
++in[v], e[u].push_back(v);
}
rep(i, 1, n) if (!in[i]) q.push(i);
int cnt = n;
while (!q.empty())
{
int u = q.top();
q.pop();
--cnt;
ans.push_back(u);
for (auto v : e[u])
if (!--in[v])
q.push(v);
}
if (cnt)
printf("-1");
else
for (auto x : ans)
printf("%d ", x);
puts("");
return 0;
}
E - Placing Rectangles
题意:给你在直角坐标系中划分出一块长为 \(X\) ,宽为 \(Y\) 的矩形区域,现给你三个面积至少为 \(A、B、C\) 的矩形,问能否在这片矩形区域中不重叠地放置这三个矩形。
题目分析:首先我们考虑只放置两个矩形的情况,设两个矩形的面积至少为 \(S\) 和 \(T\) :
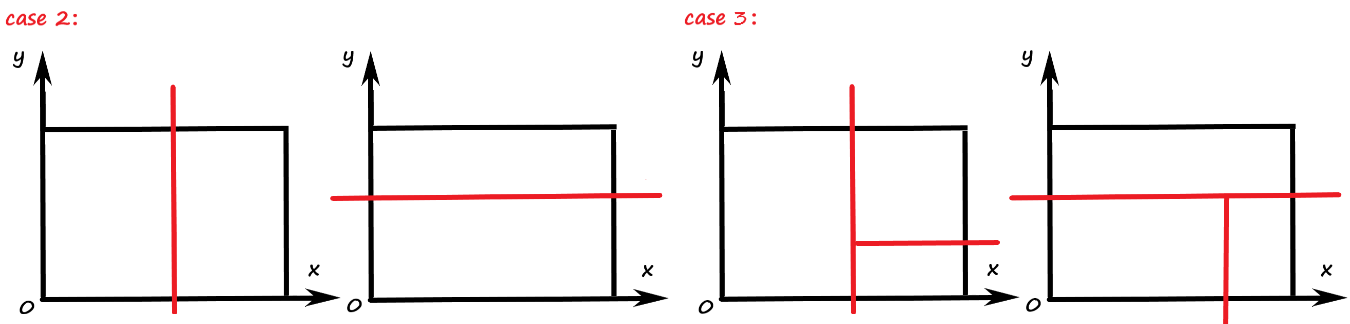
对于所有合法的放置,一定存在一条平行于 \(x\) 轴或 \(y\) 轴的直线 \(l\) ,且 \(l\) 满足以下条件:
- 不会穿过任何一个矩形
- 将矩形区域拆分为了两部分,每一部分都能放置一个矩形
如果该直线 \(l\) 存在,且与 \(x\) 轴平行,则 \(l\) 的取值 \(y=⌈\frac{S}{X}⌉\)
如果该直线 \(l\) 存在,且与 \(y\) 轴平行,则 \(l\) 的取值 \(x=⌈\frac{S}{Y}⌉\)
只需判断这两种情况,即可得出答案。
那么当我们要放置三个矩形时,实际上就是换汤不换药了,不妨对拆分出的两部分区域任选一份继续拆分,再次判断上述两种情况,这样要放置四个五个 \(n\) 个矩形都是同样的做法。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
using ll = long long;
bool solve2(ll x, ll y, ll s, ll t)
{
rep(i, 1, 2)
{
ll len = (s - 1) / x + 1;
if (len < y && x * (y - len) >= t)
return true;
std::swap(x, y);
}
return false;
}
bool solve1(ll x, ll y, ll a, ll b, ll c)
{
rep(i, 1, 2)
{
rep(j, 1, 3)
{
ll len = (a - 1) / x + 1;
if (len < y && solve2(x, y - len, b, c))
return true;
std::swap(a, b), std::swap(b, c);
}
std::swap(x, y);
}
return false;
}
int main(int argc, char const *argv[])
{
ll x, y, a, b, c;
scanf("%lld %lld %lld %lld %lld", &x, &y, &a, &b, &c);
puts(solve1(x, y, a, b, c) ? "Yes" : "No");
return 0;
}
F - Parenthesis Checking
题意:已知一个由 \(N\) 个左右括号组成的字符串 \(S\) ,你需要进行下面两种操作:
- \(1~~l~~r\) :交换 \(S\) 的第 \(l\) 和第 \(r\) 个字符
- \(2~~l~~r\) :判断区间 \([l,r]\) 内的括号序列是否合法
题目分析:线段树好题。
首先我们考虑如何判断某个长为 \(M\) 的括号序列是否合法:设 ‘(’ 为 \(+1\) ,‘)’ 为 \(-1\) ,然后对序列作前缀和 \(sum\) ,这样当且仅当 \(sum_M = 0\) 且 \(sum\) 的最小元素为 \(0\) 时序列才合法。(如 )( 这种情况区间和虽然为 \(0\) ,但是并不合法)
线段树的每个节点维护区间和 \(sum\) 与前缀和最小值 \(mn\) 。我们可以写 \(pushup\) 函数来合并两条线段:
#define lson k << 1
#define rson k << 1 | 1
void pushup(int k)
{
tree[k].sum = tree[lson].sum + tree[rson].sum;
tree[k].mn = std::min(tree[lson].mn, tree[lson].sum + tree[rson].mn);
}
为什么这样维护呢?这个问题我想了一下午,按理来说应该直接比较左右子树的前缀和最小值啊,但我们要明确的一点是:我们维护的 \(mn\) ,是前缀和的历史最小值。不妨将左右子树分别看作是某个区间的前后半段,这样后半段每有一对诸如 )( 的不合法括号时,就会使得其前缀和最小值 \(-1\) 。但是当前半段的 ‘(’ 有冗余,即 \(sum[lson] > 0\) 时,就可以和后半段无法匹配的 ‘)’ 结合成一对合法的序列从而对后半段的历史最小值产生影响,使得 \(mn+1\) 。因此合并时需要比较左子树的前缀和最小值与左子树的区间和 \(+\) 右子树的前缀和最小值,用较小的那个更新 \(mn\) 。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
const int maxn = 2e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int n, q, a[maxn];
#define lson k << 1
#define rson k << 1 | 1
struct node
{
int l, r, sum, mn;
} tree[maxn << 2];
void pushup(int k)
{
tree[k].sum = tree[lson].sum + tree[rson].sum;
tree[k].mn = std::min(tree[lson].mn, tree[lson].sum + tree[rson].mn);
}
void build(int k, int l, int r)
{
tree[k].l = l, tree[k].r = r;
if (l == r)
{
tree[k].sum = tree[k].mn = a[l];
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(k);
}
void update(int k, int p)
{
if (tree[k].l == tree[k].r && tree[k].l == p)
{
tree[k].sum = tree[k].mn = a[p];
return;
}
int mid = (tree[k].l + tree[k].r) >> 1;
p <= mid ? update(lson, p) : update(rson, p);
pushup(k);
}
node query(int k, int l, int r)
{
if (l <= tree[k].l && tree[k].r <= r)
return tree[k];
int mid = (tree[k].l + tree[k].r) >> 1;
if (r <= mid)
return query(lson, l, r);
else if (l > mid)
return query(rson, l, r);
else
{
node res, lft, rht;
lft = query(lson, l, mid), rht = query(rson, mid + 1, r);
res.sum = lft.sum + rht.sum;
res.mn = std::min(lft.mn, lft.sum + rht.mn);
return res;
}
}
int main(int argc, char const *argv[])
{
n = read(), q = read();
rep(i, 1, n) a[i] = (getchar() == '(' ? 1 : -1);
build(1, 1, n);
int opt, l, r;
while (q--)
{
opt = read(), l = read(), r = read();
if (opt == 1)
{
if (a[l] == a[r])
continue;
std::swap(a[l], a[r]);
update(1, l), update(1, r);
}
else
{
node res = query(1, l, r);
if (res.sum == 0 && res.mn == 0)
puts("Yes");
else
puts("No");
}
}
return 0;
}