【暖*墟】#数据结构# LCT的学习与练习

一. 概念总结

【 Link-Cut Tree 】一种动态维护森林上的信息 的数据结构，适用于动态树问题。

采用类似树链剖分的轻重边路径剖分，把树边分为实边和虚边，并用 Splay 来维护每一条实路径。

LCT用很多个splay维护森林的信息。因为splay是二叉树，所以要将原森林”剖分”成很多个二叉树。

于是就有实边和虚边。用实边连接起来的一棵树就是原森林中的一棵树，我们称它为原树。

按每个点在原树中的深度为优先级，将每个点以优先级的中序遍历放到splay上。

那么：每一个Splay维护的是一条从上到下按在原树中深度严格递增的路径，

如果中序遍历Splay，得到的每个点的深度序列严格递增。

我们一般将原树所对应的splay称为辅助树，原森林就对应一个辅助树森林。

那么 Link-Cut Tree 的基本操作复杂度为均摊。 ----- 来自各种 dalao orz

显然原树中同一个深度的点是不可能在一个splay里的，因此每个splay里面就是维护了原树中的一条链。

每棵 Splay 之间都用"虚边"连接(下图灰边)，每棵 Splay 中的结点都用"实边"链接起来(下图黑边)。

假如我们现在有一个例子：(用红色圈圈圈在一起的结点是一个 Splay 中的结点)

LCT

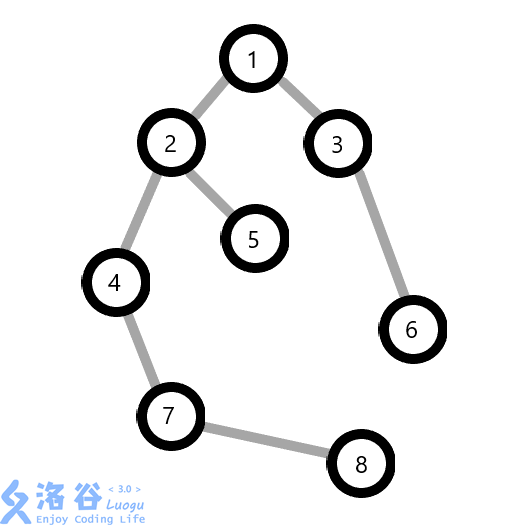
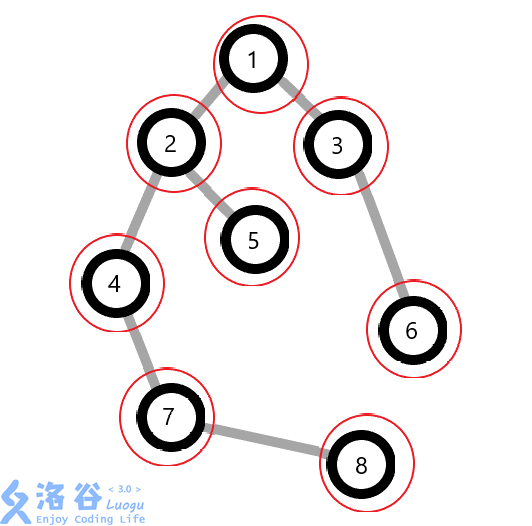
一开始，每个结点都是一颗 Splay，就像这样：

LCT

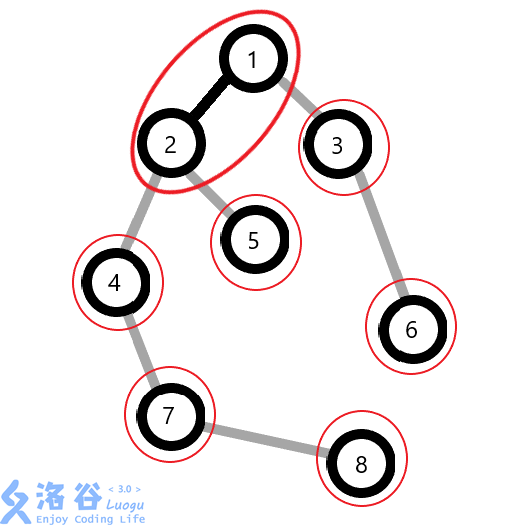
如果将1,2连接起来，那么1,2就在同一个 Splay 中：

LCT

二. 基本定义

fa[x]:结点x的爸爸(father)

v[x]:结点x的权值(value)

sum[x]:结点x及它的子树的权值和(sum)

rev[x]:结点x的翻转情况(rev)

ch[x][0/1]:结点x的左/右儿子

三. 相关操作

Link-Cut Tree 支持的基本操作

Access(x)：将x到根节点的路径上全部变成实边，并弃掉自己所有的儿子。

(变成虚边：认父不认子)(每一个父结点对于自己的每个子结点只有一条实边)

findroot(x):找出x所在的原树的根结点(实际上就是上图的一号点)。

makeroot(x):将x点变为原树的根节点；split(x,y):将x,y节点放在一个 Splay 中，方便操作。

link(x,y):将x和y所在原树合并起来(树的连接)；cut(x,y):将x和y所在原树拆开(树的切断) 。

Access(x)

将点x到原树中根结点root之间的链，放到一个辅助树splay中。

即：将x到根节点的路径上全部变成实边，并弃掉自己所有的儿子。

LCT

执行 Access(6) 。即：将{1--3，3--6}变成实边，1-2变成虚边。

假设6有一儿子n，之间用实边连着，那么这条边也将变成虚边。

即：每次将

   Q：为什么是右儿子而不是左儿子呢？

   A：因为f[x]的深度小于x，而在Splay里面f[x]是x的爸爸，所以x在Splay中是f[x]的右儿子。

所以就变成了这样：

LCT

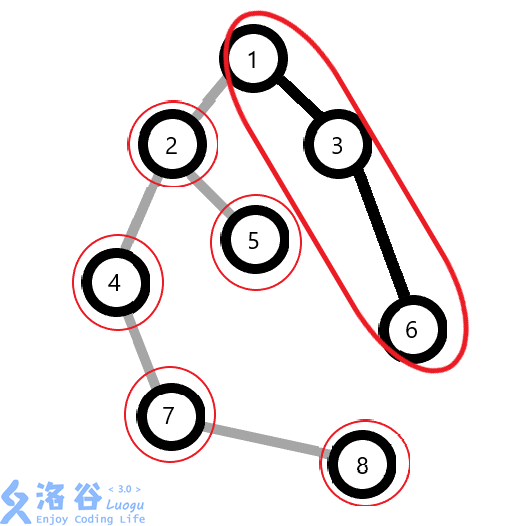
1.转到根。 2.换右儿子。3.更新信息。4.当前操作点切换为轻边所指的父亲，转1。

我真的不知道自己到底是哪里来的勇气...觉得自己能学会LCT？？？

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

/* p3690【模板】Link Cut Tree（动态树） */

/* 给定n个点以及每个点的权值，处理m个操作。
0：询问从x到y路径上的点权xor值。保证x到y是联通的。
1：连接x到y。若x到y已经联通，则无需连接。
2：删除边(x，y)。不保证边(x，y)存在。3：将点x上的权值变成y。 */

void reads(int &x){ //读入优化（正负整数）
    int fx=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();}
    x*=fx; //正负号
}

const int N=300019;

int fa[N],ch[N][2],v[N],s[N],sta[N]; bool r[N];

//【维护の基本操作】////////////////////////////////////

bool nroot(int x){ //判断节点是否为一个Splay的根（与普通Splay的区别1）
    return ch[fa[x]][0]==x||ch[fa[x]][1]==x;
} //原理：如果连的是轻边，他的父亲的儿子里没有它。

void push_up(int x){ s[x]=s[ch[x][0]]^s[ch[x][1]]^v[x]; } //上传信息
    
void push_rev(int x){int t=ch[x][0];ch[x][0]=ch[x][1],ch[x][1]=t;r[x]^=1;} //翻转操作

void push_down(int x){ //判断并释放懒标记
    if(r[x]){ if(ch[x][0])push_rev(ch[x][0]);
        if(ch[x][1])push_rev(ch[x][1]); r[x]=0; } }

//【splay基本操作】/////////////////////////////////////

void rotate(int x){ //一次旋转
    int y=fa[x],z=fa[y],k=(ch[y][1]==x),w=ch[x][!k];
    if(nroot(y)) ch[z][ch[z][1]==y]=x; ch[x][!k]=y; ch[y][k]=w;
    //↑↑额外注意if(nroot(y))语句，此处不判断会引起致命错误（与普通Splay的区别2）
    if(w) fa[w]=y; fa[y]=x; fa[x]=z; push_up(y);
}

void splay(int x){ //所有操作的目标都是该Splay的根（与普通Splay的区别3）
    int y=x,z=0; sta[++z]=y;
    //sta为栈，暂存当前点到根的整条路径，push_down时一定要从上往下放标记（与普通Splay的区别4）
    while(nroot(y)) sta[++z]=y=fa[y];
    while(z) push_down(sta[z--]);
    while(nroot(x)){ y=fa[x];z=fa[y];
        if(nroot(y)) rotate((ch[y][0]==x)^(ch[z][0]==y)?x:y); rotate(x);
    } push_up(x);
}

//【1】///////////////////////////////////////////////

void access(int x){ for(int y=0;x;x=fa[y=x]) splay(x),ch[x][1]=y,push_up(x);}

/*  access(x)：将根节点到x上的边都变为实边。
    1.将节点转到所属Splay的根。//splay(x)
    2.将其右儿子删除-->删一个Splay的根节点。//ch[x][1]=y
    3.更新节点信息。//push_up(x)
    4.将当前点变为虚边所指的父亲，转回步骤1。//x=fa[y=x]    */

//【2】///////////////////////////////////////////////

void makeroot(int x){ access(x); splay(x); push_rev(x); }

/*  makeroot(x)：将x成为[原树]的根节点（换根）。
    1.进行access(x)，得到一条从根节点到x的链，x在这个Splay中深度最大。
    2.这个Splay中，没有比x深度更大的点，即x没有右子树。
      直接翻转整个Splay，使得所有点的深度都倒过来。//splay(x);
      那么x就没有了左子树，x成为深度最小的点，也就是根节点。
    3.最后，给这个Splay打上翻转标记。//push_rev(x);           */

//【3】///////////////////////////////////////////////

int findroot(int x){ //找在原树中的根
    access(x); splay(x);
    while(ch[x][0]) push_down(x),x=ch[x][0];
    splay(x); return x; }

/*  findroot(x)：找到原树中的根，用于判断两点之间的连通性。 
    1.一棵树的根节点一定是深度最小的点。用access(x)把x和根连成一条链。
    2.用splay(x)将x旋转到Splay的根节点。//splay(x);
    3.根节点一定是x不断往左走得到的（越往左深度越小）。//x=ch[x][0];
    4.在往左走的过程中，一定要下传标记。//push_down(x);             */

//【4】///////////////////////////////////////////////

void split(int x,int y){ makeroot(x),access(y),splay(y); } //（0）

/*  split(x,y)：提取路径。得到x到y的一条路径，其中y是此路径所在Splay的根节点。
    1.先把x作为根节点； 2.得到根节点到y的链； 3.将y旋转到Splay的根。 */

//【5】///////////////////////////////////////////////

void link(int x,int y){ makeroot(x); if(findroot(y)!=x) fa[x]=y; } //（1）

/*  link(x,y)：连一条虚边(x,y)（如果已经连通则不操作）。
    1.将x变成原树的根，将x的父节点直接设为y（这样x、y就相连了）。
    2.在findroot(y)中执行了access(y)和splay(y)，y已经是所在Splay的根节点。
    3.连通性的检查：x成为根节点后，如果findroot(y)==x，则说明x,y连通。      */

//【6】///////////////////////////////////////////////

void cut(int x,int y){ makeroot(x);
    if(findroot(y)==x&&fa[y]==x&&!ch[y][0])
     { fa[y]=ch[x][1]=0; push_up(x); } } //（2）

/*  cut(x,y)：切断边(x,y)（如果没有边则不进行操作）。
    先把x变成根节点。如果存在边(x,y)，那么x的深度一定比y小，则x是y的左儿子。
    
    【判断】若不存在边(x,y)：1.x,y不在同一棵树内；2.x的父亲不是y，即x,y没有连边。
    3.x的右子树非空，那么以y为根的中序遍历中x和y不相邻，即没有边相连。*/

//【主程序】///////////////////////////////////////////////

int main(){
    int n,m; reads(n),reads(m);
    for(int i=1;i<=n;i++) reads(v[i]);
    while(m--){ int op,x,y; reads(op),reads(x),reads(y);
        if(op==0) split(x,y),printf("%d
",s[y]);
        if(op==1) link(x,y); //连一条虚边(x,y)
        if(op==2) cut(x,y); //切断边(x,y)
        if(op==3) splay(x),v[x]=y; //把x旋转到根再修改
    }
}

——时间划过风的轨迹，那个少年，还在等你

【暖*墟】#数据结构# LCT的学习与练习

一. 概念总结

二. 基本定义

三. 相关操作

Link-Cut Tree 支持的基本操作