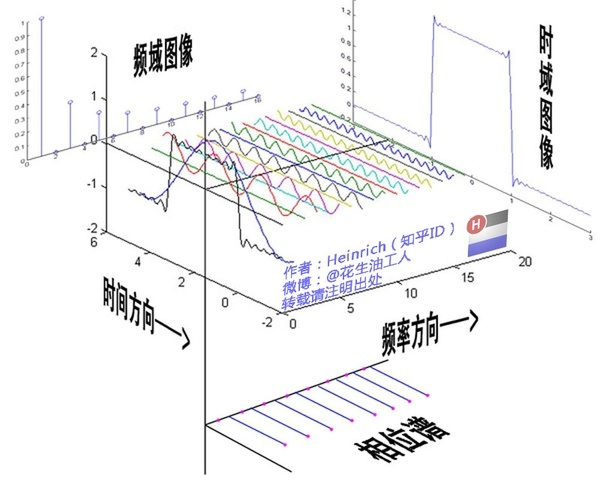
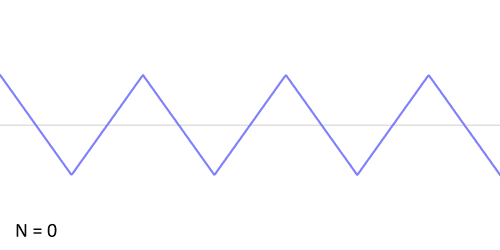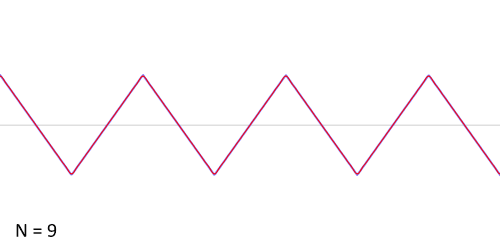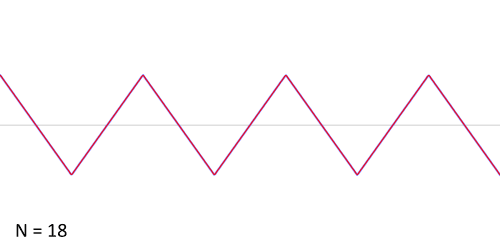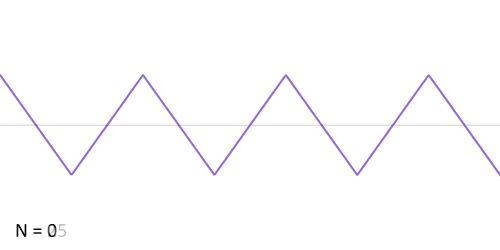
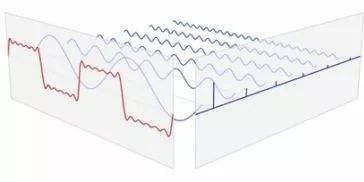
傅立叶变换(的三角函数形式)的基本原理是:多个正余弦波叠加(蓝色)可以用来近似任何一个原始的周期函数(红色)
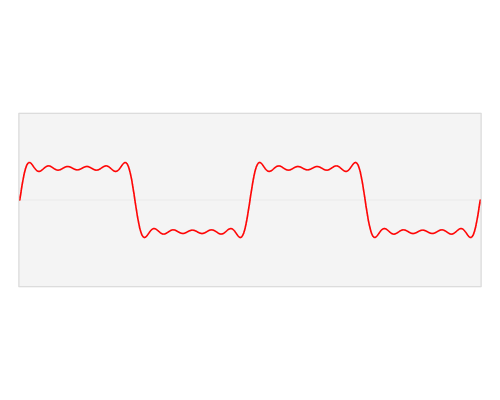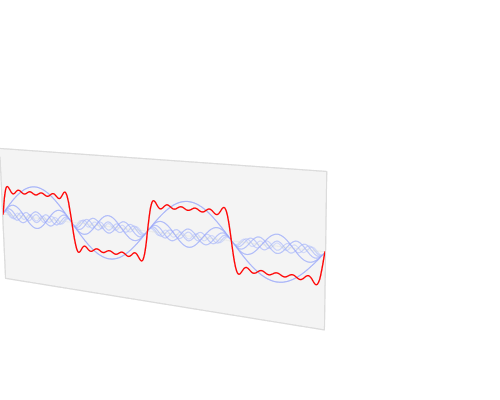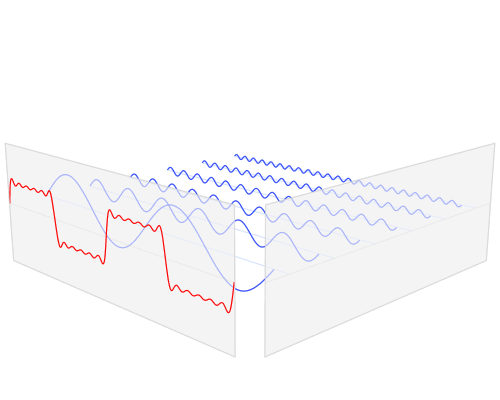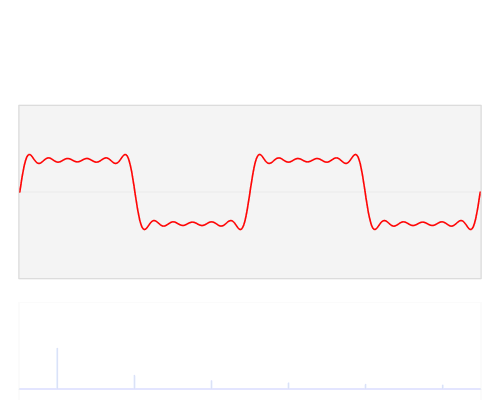
你可以简单地理解为,我们去菜市场买菜的时候,无论质量如何奇怪,都可以转变为“5个 1 斤的砝码,2个 1 两的砝码”来表示出来,那么上面的图我们也可以近似地想象成周期函数就是质量特别奇怪的物品,而正余弦波就是想像成成“我用了5个1号波、3个2号波”来表示这个周期函数。
我们日常遇到的琴音、震动等都可以分解为正弦波的叠加,电路中的周期电压信号等信号都可以分解为正弦波的叠加。那么接下来,我们再深入讲一下,我们再来了解两个概念,时间是永远在流动的花谢花开、潮来潮往,世界永远在不停地变化,而以时间为参照系去看待这个世界,我们就叫它时域分析。就好像心电图一样,心电图是记录心脏每一心动周期所产生的电活动变化,所以随着时间变化心电图也会变化。这就是时域。
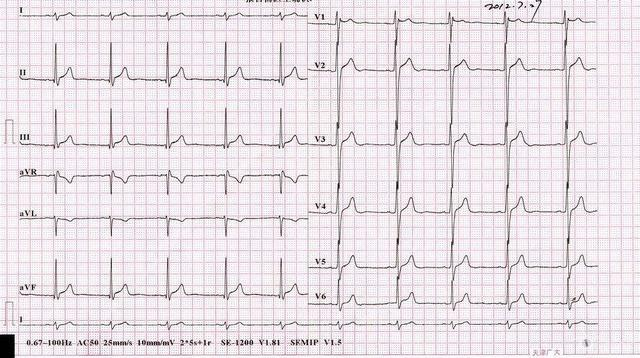
而频域呢,就是描述信号在频率方面特性时用到的一种坐标系,频域就是装着正弦函数的空间,自然而然的,正余弦波是频域中唯一存在的波形。
我们从时域我们可以观察到心脏随着时间变化在不停地跳动的情形,但是从频域来看,就是一个简单的心电图符号。如果时域是运动永不停止的,那么频域就是静止的。
在很多领域我们都可以用到时域和频域,在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。

刚刚我们讲了多个正余弦波叠加可以用来近似任何一个原始的周期函数,我们心脏不同时间、不同强度的跳动就成了我们所看到的心电图。就可以看作正余弦波叠加成的周期函数。同样的,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲,也可以看作余弦波叠加成的周期函数。


而对于信号来说,信号强度随时间的变化规律就是时域特性,信号是由哪些单一频率的信号合成的就是频域特性傅里叶变换实质涉及的是频域函数和时域函数的转换。
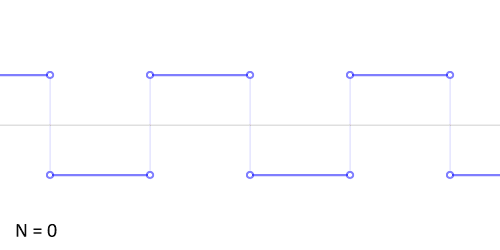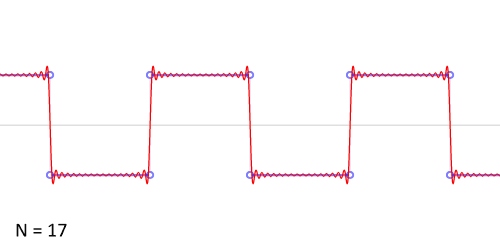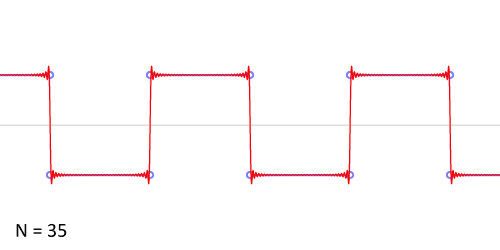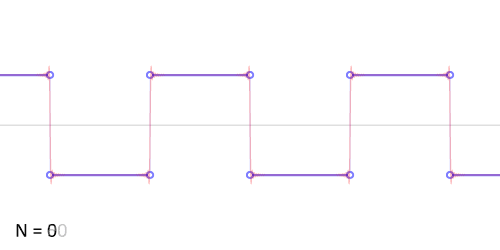
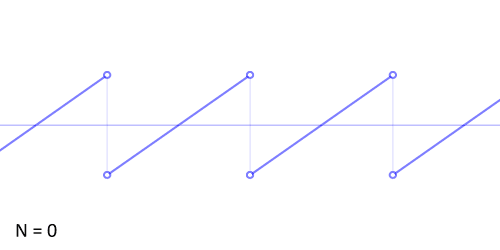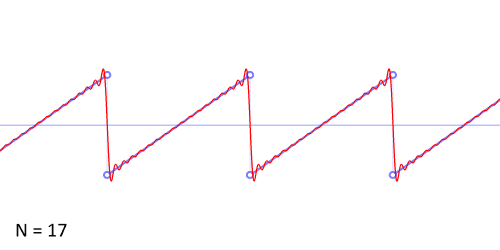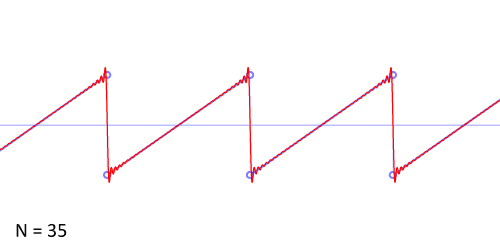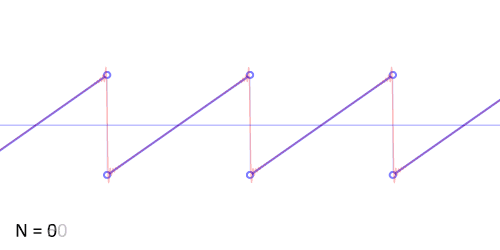
那么正余弦波是如何叠加成周期函数的呢?随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,不仅仅是矩形,你能想到的任何波形都是可以如此方法用正余弦波叠加起来的。
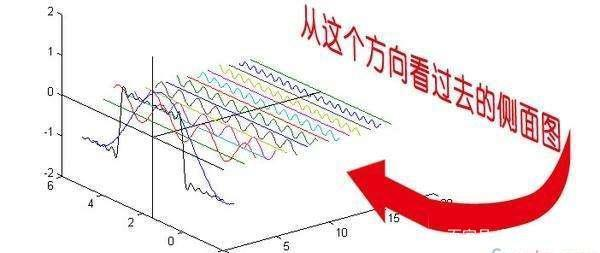
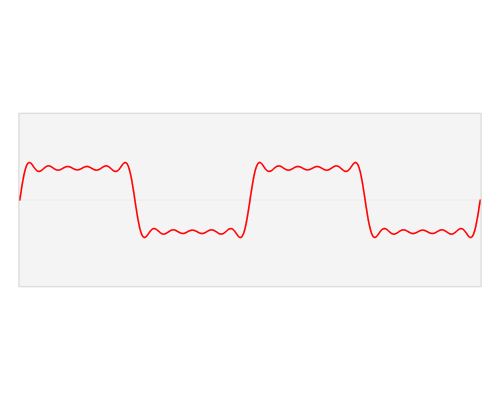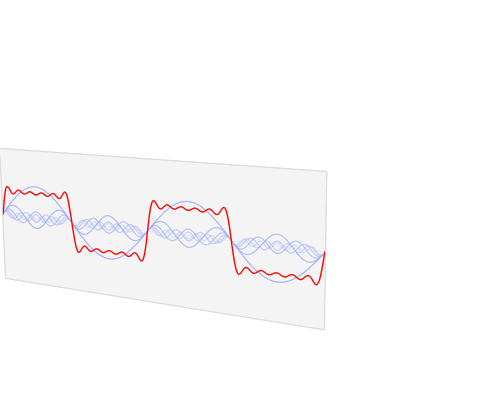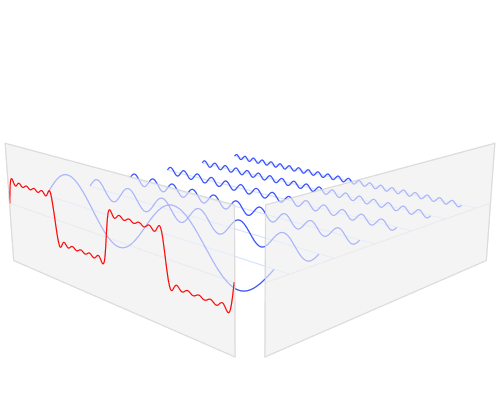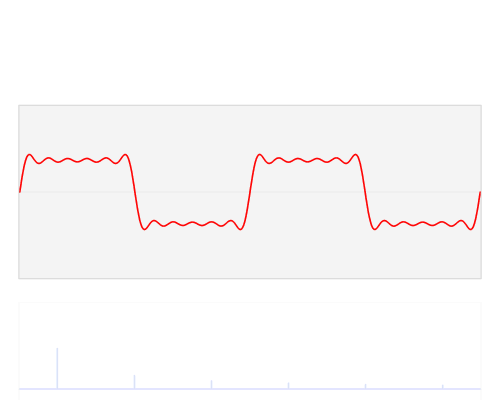
从这个方向看过去的侧面图就是频域
从时域来看,我们会看到一个近似为矩形的波,而我们知道这个矩形的波可以被差分为一些正弦波的叠加。而从频域方向来看,我们就看到了每一个正余弦波的幅值,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为 0 的正弦波!也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准 90 度角的矩形波呢?不幸的告诉大家,答案是无穷多个。
所以,我们可以再来看一下开头的动图,是不是就更加能够理解了。
而想要完美地表示正余弦波,除了正余弦波的幅值是不行的,还需要相位谱的帮忙,什么是相位呢?就是对于一个波,特定的时刻在它循环中的位置:一种它是否在波峰、波谷或它们之间的某点的标度。
不同相位决定了波的位置,所以对于频域分析,仅仅有幅值是不够的,我们还需要一个相位谱。频谱的重点是侧面看,相位谱的重点则是从下面看。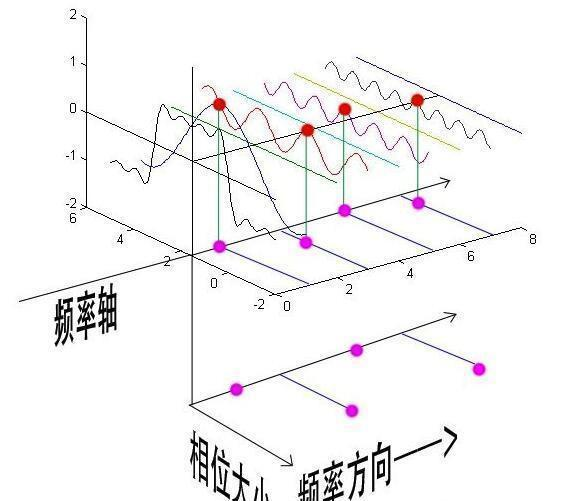
如上图所示:投影点我们用粉色点来表示,红色的点表示离正弦函数频率轴最近的一个峰值,而相位差就是粉色点和红色点水平距离除以周期。将相位差画到一个坐标轴上就形成了相位谱。
总结一下,傅立叶变换就是多个正余弦波叠加可以用来近似任何一个原始的周期函数,它实质是是频域函数和时域函数的转换。而其中时域就是永远随着时间的变化而变化的,而频域就是装着装着正余弦波的空间,代表着每一条正余弦波的幅值,而表示正余弦波除了幅值是不够的,就还有相位谱。

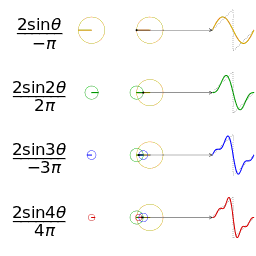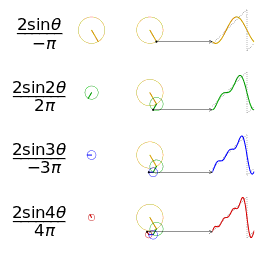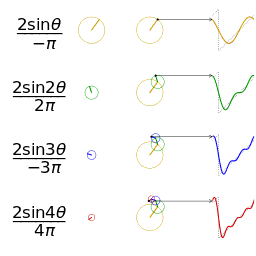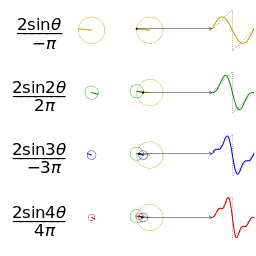
傅里叶级数(Fourier Series)的相位谱
上一章的关键词是:从侧面看。这一章的关键词是:从下面看。
在这一章最开始,我想先回答很多人的一个问题:傅里叶分析究竟是干什么用的?这段相对比较枯燥,已经知道了的同学可以直接跳到下一个分割线。
先说一个最直接的用途。无论听广播还是看电视,我们一定对一个词不陌生——频道。频道频道,就是频率的通道,不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事:
先在纸上画一个sin(x),不一定标准,意思差不多就行。不是很难吧。
好,接下去画一个sin(3x)+sin(5x)的图形。
别说标准不标准了,曲线什么时候上升什么时候下降你都不一定画的对吧?
好,画不出来不要紧,我把sin(3x)+sin(5x)的曲线给你,但是前提是你不知道这个曲线的方程式,现在需要你把sin(5x)给我从图里拿出去,看看剩下的是什么。这基本是不可能做到的。
但是在频域呢?则简单的很,无非就是几条竖线而已。
所以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
再说一个更重要,但是稍微复杂一点的用途——求解微分方程。(这段有点难度,看不懂的可以直接跳过这段)微分方程的重要性不用我过多介绍了。各行各业都用的到。但是求解微分方程却是一件相当麻烦的事情。因为除了要计算加减乘除,还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法,大学数学瞬间变小学算术有没有。
傅里叶分析当然还有其他更重要的用途,我们随着讲随着提。
————————————————————————————————————
下面我们继续说相位谱:
通过时域到频域的变换,我们得到了一个从侧面看的频谱,但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少,而没有提到相位。基础的正弦波A.sin(wt+θ)中,振幅,频率,相位缺一不可,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。那么这个相位谱在哪呢?我们看下图,这次为了避免图片太混论,我们用7个波叠加的图。
鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰,而这个波峰所处的位置离频率轴有多远呢?为了看的更清楚,我们将红色的点投影到下平面,投影点我们用粉色点来表示。当然,这些粉色的点只标注了波峰距离频率轴的距离,并不是相位。
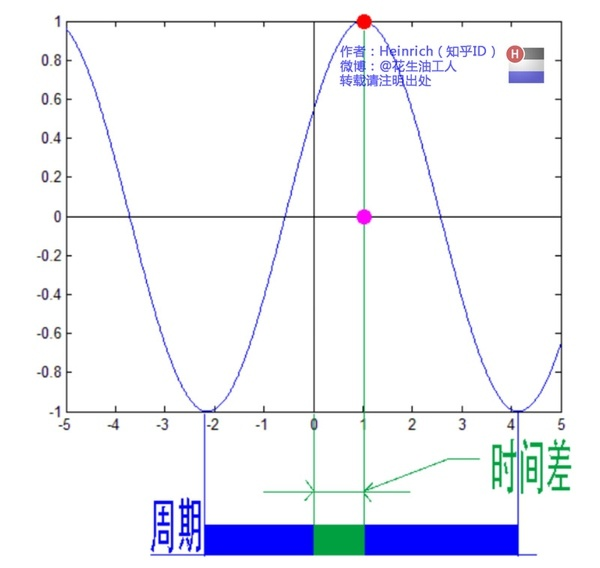
这里需要纠正一个概念:时间差并不是相位差。如果将全部周期看作2Pi或者360度的话,相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi,就得到了相位差。
在完整的立体图中,我们将投影得到的时间差依次除以所在频率的周期,就得到了最下面的相位谱。所以,频谱是从侧面看,相位谱是从下面看。下次偷看女生裙底被发现的话,可以告诉她:“对不起,我只是想看看你的相位谱。”
注意到,相位谱中的相位除了0,就是Pi。因为cos(t+Pi)=-cos(t),所以实际上相位为Pi的波只是上下翻转了而已。对于周期方波的傅里叶级数,这样的相位谱已经是很简单的了。另外值得注意的是,由于cos(t+2Pi)=cos(t),所以相位差是周期的,pi和3pi,5pi,7pi都是相同的相位。人为定义相位谱的值域为(-pi,pi],所以图中的相位差均为Pi。