其实也不是多难的知识点吧……学了一个中午+半个下午就把它学会了(做过那道 jxd 作业 CF571D 的应该比较好理解)
Kruskal 重构树大概就是在正常 Kruskal 的时候,对于两个需要连边的点 (u,v) 不直接连边,而是新增一个虚拟节点 (T),权值为 (u,v) 间的边权 (w),并连边 (T o u,T o v)。
下图可以较为清楚地展示 Kruskal 重构树的过程,正常的 Kruskal 我们是这样连边的:

而 Kruskal 重构树我们是这样连边的:
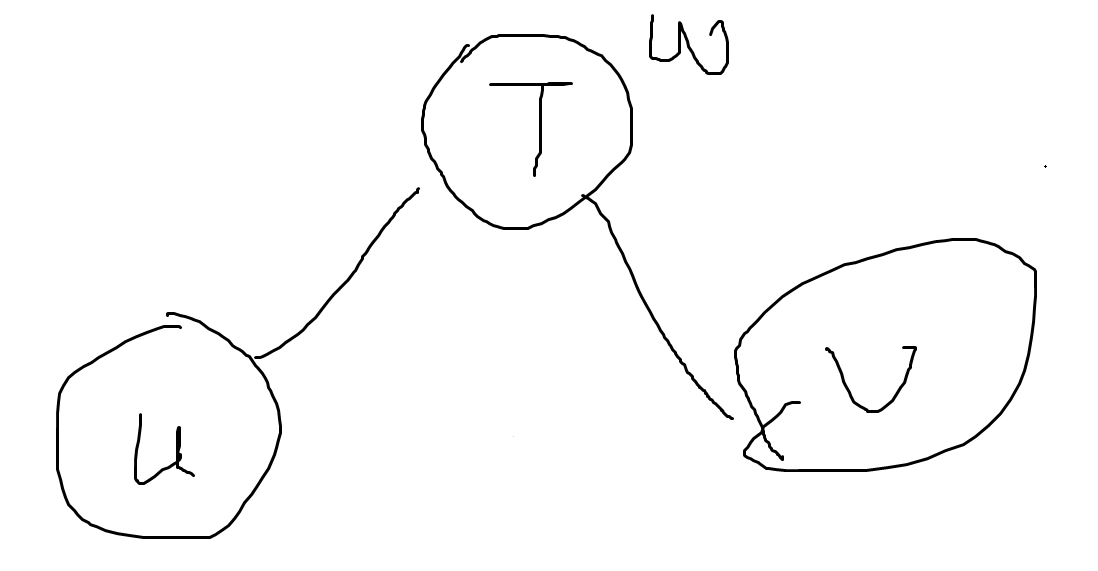
显然这样建出来的图是一棵树,而这棵树有以下性质:
- 由于我们每个新建的点都恰好连出的两条边,因此这棵树是一个二叉树
- 由于我们是按照边权从小到大排序来建树的,因此这棵树的权值可以看作一个大根堆(假设叶子节点的权值为 (0) 或 (-infty))
- 对于两个点 (u,v),它们之间路径最大值的最小值就是 Kruskal 重构树上它们 LCA 的权值,这个用普通的 Kruskal 建出最小生成树再查询它们之间路径权值最大值的方法也可说明
- 对于一个点 (u),记 (v) 为离 (u) 最远的满足 (v) 的权值 (le w) 的 (u) 的祖先,那么所有 (u) 经过权值 (le w) 的边能够到达的点的集合恰好为 (v) 子树内所有叶子节点,这个性质相当重要,因为它可以将我们陌生的图的连通性问题转化为熟悉的子树问题,而这恰恰是可以通过 DFS 序套上某些数据结构维护的。
Kruskal 重构树的知识点就这么多,实现起来不算太难,只不过有以下需要注意的地方:
- Kruskal 重构树点数最多会达到 (2n-1),因此要开两倍空间
- 如果题目图不连通,那么最后建出的 Kruskal 重构树也不连通,也就是说最后得到的是一个二叉森林,此时就要额外补上一个节点 (R),权值为 (infty),并将 (R) 与森林中所有连通块的根节点之间连边(当然这样得到的树就不是二叉树了)
代码想想还是贴一下罢(当然这是题目保证连通的情况的代码,如果题目没保证连通那后面还要加上两三句话,由于过于简单就不贴了):
int hd[MAXN*2+5],nxt[MAXN*2+5],to[MAXN*2+5],ec=0;
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
int f[MAXN*2+5],nc;
int main(){
nc=n;for(int i=1;i<=n;i++) f[i]=i;
for(int i=1,u,v;i<=m;i++){
u=find(u);v=find(v);if(u==v) continue;++nc;
f[u]=f[v]=f[nc]=nc;adde(nc,u);adde(nc,v);val[nc]=i;
}
}
总之,Kruskal 重构树无法解决权值之和最小的问题,它只能解决路径上权值最大值最小或最小值最大的可达性问题,因此看到类似于”只经过权值 (le w) 的边“或者”能够到达的点当中“等字眼就可以联想到 Kruskal 重构树。
例题:
1. AT1998 [AGC002D] Stamp Rally
差点不会做,身败名裂
首先以边的编号为权值建出 Kruskal 重构树,对每个询问考虑二分,二分答案 (mid),那么显然可以倍增找出 (x) 可以到达的点和 (y) 可以到达的点,显然是两个子树 (u) 和 (v) 的并,而这个并的大小可用通过判断 (u,v) 是否存在祖先关系求出,如果存在就是祖先子树大小,否则就是 (siz_u+siz_v),将它与 (z) 比较即可。
时间复杂度 (nlog^2n),可能有 (nlog n) 的做法,不过估计 Kruskal 重构树是做不了了(
u1s1 倍增是真的喜欢和 Kruskal 重构树贴贴(大雾
2. P4197 Peaks
还是建出 Kruskal 重构树,倍增找出对应子树 (u),然后建立主席树,在主席树上离散化+二分找第 (k) 大即可。
时间复杂度 (nlog n)。
好套路啊……
3. CF1416D Graph and Queries
考虑离线,对每条边记它的边权为它被删除的时间(如果没被删除则为 (q+1)),然后建 Kruskal 重构树(这次要建个大根堆,因为可以访问的边的边权要大于某个数),然后对每个询问还是倍增找出它可以到达的点,然后线段树+DFS 序找出子树内权值最大的点赋为 (0) 即可。
时间复杂度 (nlog n)。
4. P4768 [NOI2018] 归程
首先最优方案肯定是开一段距离的车然后走一段距离,而由于终点都是 (1) 且图为无向图,因此可以 dijkstra(关 于 S P F A,它 死 了,死 于 这 道 题 的 手 中)求出 (1) 到每个点的最短距离 (dis_i),那么每个询问的答案就是 (v) 能到达的点中 (dis) 的最小值,这个显然是可以 Kruskal 重构树解决的,而且甚至不用什么数据结构(不愧是你 NOI 签到题),直接记录一个子树最小值即可。
时间复杂度 (Tnlog n)。
5. P4899 [IOI2018] werewolf 狼人
我竟然能独立想出来近几年 IOI 的题,incredible!
首先题目等价于能否找到一个编号在 ([L_i,R_i]) 之间的点 (t),满足存在 (U_i o t),只经过编号 (ge L_i) 的点的路径,也存在 (t o V_i),只经过编号 (le R_i) 的路径。
这东西显然是可以 Kruskal 重构树的,比较棘手的一点是此题涉及点权,而不是边权。不过事实上转化非常容易,显然对于一条边 ((u,v)) 而言,只有 (u,v) 的权值都符合要求,((u,v)) 才能通过,那么我们就可以把 ((u,v)) 的权值设为 (min(w_u,w_v))(如果要求经过的边权值 (ge v))或者 (max(w_u,w_v))(如果要求经过的边权值 (le v)),这样就可以 Kruskal 重构树了。
于是现在题目转化为,对于有两棵树,(q) 组询问,每组询问给出第一棵树上的点 (u) 和第二棵树上的点 (v),判断是否存在一个叶子节点在 (u,v) 的子树中,这个可以使用 DFS 序转化为区间问题,然后就可以主席树维护了,有点类似于这个题,时间复杂度 (nlog n)