今天学习了一下上次集训讲的置换,当时没懂,这个东西确实难理解。。。我看了《算法竞赛入门经典训练指南》,才勉强明白一点基础。。。
学习置换之前先要理解群论:
给定一个集合G={a,b,c…}和集合G上的一个二元计算*,满足以下四个条件:
(1)封闭性
若a,b∈G,则存在唯一确定的c∈G,使得a*b=c;
(2)结合律成立
任意a,b,c∈G,有(a*b)* c=a* (b*c);
(3)单位元存在
存在e∈G,对任意a∈G,满足a*e=e*a=a,称e为单位元,也称幺元;
(4)逆元存在
任意a∈G,存在唯一确定的b∈G, a*b=b*a=e(单位元),则称a与b互为逆元素,简称逆元,记作a^(-1)=b.
通常称G上的二元运算*为“乘法”,称a*b为a与b的积,并简写为ab.
若群G中元素个数是有限的,则G称为有限群。否则称为无限群。有限群的元素个数称为有限群的阶。
了解群论之后才进行初步置换。
先举个例子:

表示1被1到n中的某一个数a1取代,2被1到n中的某一个数a2取代,直到n被1到n中的某一个数an取代,且a1到an各不相同 置换群
置换群的元素是置换,运算的置换的连接

还可以进行拆分:
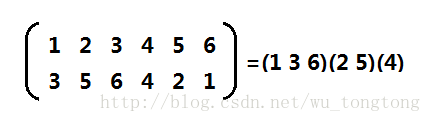
其实就是几个元素进行轮换。
例题:
等价类计数问题
有这样一个经典问题,给2*2方格中涂黑白两色,有几种方案
Ans.16

但是如果定义一种“旋转操作”,规定逆时针旋转90°,180°,270°后相同的方案算作一种,
那么答案就变成6种了
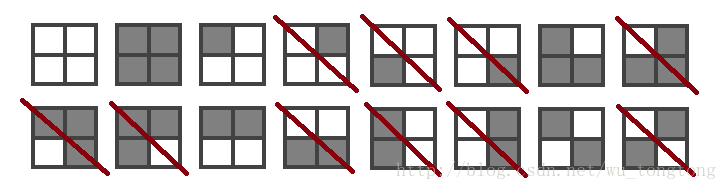
这类问题被称作是等价类计数问题
也就是说,题目中会定义一种等价关系,满足等价关系的元素被看做是同一类
对于一个置换f,若一个方案经过置换后不变,称s为f的不动点
将f的不动点的数目记为C(f),则有
Burnside 定理
等价类数目为所有C(f)的平均值
例如在本题中,
“逆时针旋转180°”的不动点:

“逆时针旋转90°”的不动点:

“逆时针旋转270°”的不动点:

“逆时针旋转0°”的不动点:
根据Burnside引理,答案是(16+2+2+4)/4=6
