概要：
1. 介绍Logistic Regression的数学模型，推导并详细解释求解最优回归系数的过程；
2. Python实现Logistic Regression的基本版；
3. 介绍sklearn中的Logistic Regression算法及其关键参数；
4. 实现一个基于Logistic Regression的简单选股策略
1.学习机器学习的动机
詹姆斯·西蒙斯在TED的对话中有提到：
Q：机器学习在这里扮演了怎样一个角色？
A：某种意义上，我们做的就是机器学习。你观察一大堆数据，模拟不同的预测方案，
直到你越来越擅长于此。我们所做之事，不见得一定有自我反馈，但确实有效。
视频地址：与横扫华尔街数学家的珍贵对话
现在有许多已实现的机器学习开源包可供我们调用，如sklearn，更高级的技术还有Hadoop、Spark等等。那么是不是我们只须知道如何将训练数据与测试数据输入到模型，然后调用分类或回归的结果就好了呢？理解其数学原理，自己再实现一遍算法有无必要呢？
在汲取一些前辈的建议以及结合自己的思考后，我觉得自己亲手推一遍数学公式，再用Python实现算法还是有必要的。因为这样不仅能使我们加深对机器学习本质的理解，还能让我们对模型与数据之间联系更加敏感。例如，如何选择模型、如何选择特征、如何调整参数等等。
其次，目前开源的机器学习算法包提供的都是通用型的算法，并非针对量化投资这一领域来进行优化。所以，当有必要时，我们须根据自己的需求来优化这些通用算法，甚至重写。另一方面，真正有用的算法在量化领域是不会开源的。
当然机器学习这么多的算法也没有必要全都实现一遍，但常见的算法的核心部分还是要亲手实现的。
原文作者凭借着内心的兴趣想扎扎实实地学习机器学习与量化投资的知识，并且希望将来能将两者结合起来做出一些有效的模型或策略。
文中以一名工科生自学笔记的方式呈现，笔记详细记录了Logistic Regression的数学原理与推导过程。在核心公式推导过程中，都会引出并详细解释关键的求解技巧和对应的数学知识。因此，只要是对本科高数还有记忆的同学都能完全理解和掌握。希望感兴趣的朋友多多交流、指正。
2.什么是Logistic Regression
首先，我们知道机器学习是一系列对数据执行分类、回归和聚类等操作的统计算法的统称，这些算法根据历史数据（训练数据）的特征，来对未来数据（测试数据）进行判断。文中介绍的是一种最常用也最重要的分类算法—Logistic Regression。
首先我们引入对数几率函数（logistic function）：
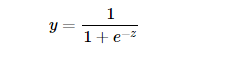此函数可将定义域为(-∞, +∞)自变量z映射到(0,1)区间。若以 y=0.5为阈值，我们可以利用这个函数实现一个二分类器：
- 当 z>0 ( y>0.5)，将其划分为1类；
- 当 z<0 ( y<0.5)，将其划分为0类。
由于于输出y为0到1之间的连续值，我们也可以认为函数是对类别的概率估计。
2.1 若有多个输入变量？
那么z由下列公式表示：
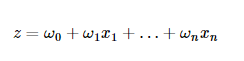
其中表示第i个输入变量的权重或是回归系数，第一个输入变量
默认为1。
上述公式的向量形式又如下公式表示：
其中，ω与x均为n行1列的列向量。
2.2 为什么称有如此形式的函数为对数几率函数？
通过简单的推导，Logistic函数可以写成如下形式：
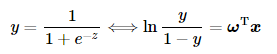其中ln便称为对数几率（log odds）。“几率”（odds）反映了输入向量x被划分为1类的相对可能性。
因此上述公式意义是用线性回归模型去描述类别的对数几率。
2.3 如何求解回归模型中的最优回归系数（权重）？
首先根据上面公式我们可得：
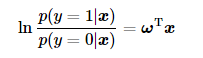进一步我们不难得到在输入为x的情况下，输出类别y分别为1和0的概率为：
2.3.1 极大似然估计 是求解最优系数的常用方法之一
极大似然估计的思想为：对于所有的抽样样本，使它们联合概率达到最大的系数便是统计模型最优的系数。因此对于第i个输入数据，它被划分为
的概率可由如下公式表示：
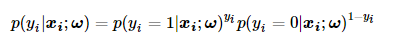上述公式的巧妙之处在于，当=1时，p
=1；而当
=0时, p(
=1|
;ω)
=1。
在极大似然法中，我们假设样本之间都是独立同分布的，因此它们的联合概率就是它们各自概率的乘积。因此关于回归系数ω的极大似然函数可由下面公式表示：
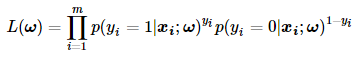为了便于计算，我们对上述公式两边同时取对数：
根据对数的性质，可以逐步写成如下形式：
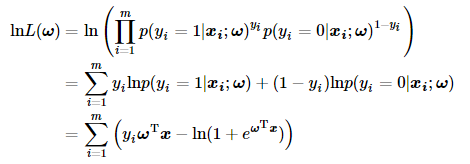
2.3.2 如何求解最优的回归系数 ω？
有两种经典的数值优化算法：a) 梯度上升法；b) 牛顿法。
a) 梯度上升法：
函数在某一点的梯度总是指向该函数增长最快的方向。因此沿着该函数的梯度方向探寻就能找到该函数的最大值。梯度上升法的迭代公式如下：
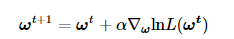公式中 α表示每次迭代的步进。∇ω表示梯度算子。
根据以上定义，我们求取梯度首先方程两边同时取微分：
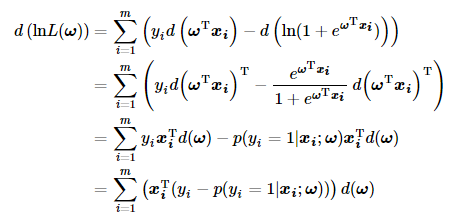因此之前公式中的梯度最终可写成如下的形式：
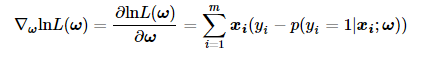上文求解中有两处向量微分运算的小技巧：
第一处：由于为标量，我们取转置后，其性质不变。
第二处：在向量的微分运算中，梯度与导数矩阵是相互装置的关系。
所以公式（12）的在公式（13）中变为
。
b) 牛顿法：其原理是利用泰勒公式不断迭代，从而逐次逼近零点或极值点。
一阶展开求零点：我们知道泰勒公式在处的一阶展开如下所示：
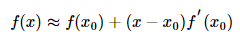我们用一阶展开式求解函数的零点：
稍作整理，可写成如下形式：
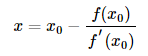由于一阶展开式只是与原函数近似相等，因此上述公式中的x并非函数的零点，而只是比更接近零点。因此通过对上述公式迭代可以不断逼近函数零点。
如果是求函数的极值点
那就要用到泰勒二阶展开式：
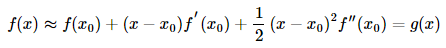知道函数在其一阶导数等于0时取到极值，因此我们求上式g′(x)=0的解：
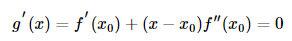通过同样整理上式，可得：
如果输入是多维的变量
高维情况的牛顿法迭代公式与上面类似，其如下所示：
其中∇f()表示的是函数f(
)的梯度，
表示的是函数的 Hessian矩阵的逆矩阵。
当输入变量为一维时，Hessian矩阵其实可以理解为变量的二阶导数。其Hessian矩阵的定义如下：
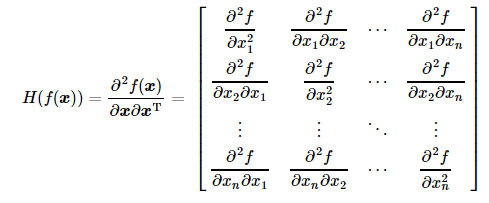梯度上升法与牛顿法的比较：
梯度法是一阶收敛的，而牛顿法是二阶收敛的。因此牛顿法的迭代次数要少于梯度法，然而Hessian的逆矩阵的计算会增加算法的复杂度。这个问题又可以通过Quasi-Newton方法解决，在本文中不zai深入讨论。
3. Python实现Logistic Regression的基本版
选择牛顿法求解Logistic Regression中的最优回归系数。根据牛顿法迭代上述式子和Hessian矩阵的定义，把Logistic Regression中的回归系数迭代更新公式为：
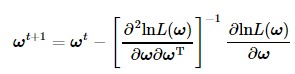其中∂lnL(ω)/∂ω在之前已求得，而对∂2lnL(ω)/∂ω∂ωT的求解可按照上文所提到的两条向量微分运算方法来计算，因此：
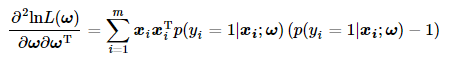好了！到此迭代公式已经完全掌握了，现在该实现算法了！
3.1 准备数据：
从网上整理了一组数据: 前两列元素是feature；最后一列是label，其值是0或1。
3.2 数据预处理，包括：
1.增加常数项: 1.0；
2.feature 与 label的分离；
3.返回数组类型的feature和label。
3.3 定义Logistic函数：
3.4 梯度上升法算法：
下面给出了梯度上升法的算法实现。
上述算法的倒数第三行，我们用矩阵形式表示梯度上升法的迭代公式，其具体数学形式如下：
3.5 牛顿法算法：
与上小节3.4一致，我们都用矩阵形式表示迭代公式。其中梯度的具体数学形式在上小节已给出。在本节的牛顿算法中，Hessian矩阵具体数学形式如下：
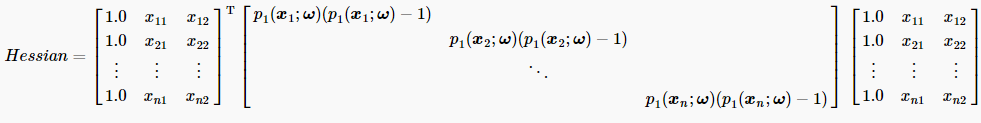
3.6 选择最优算法，根据求得的最优系数画出回归直线：
3.7 下面一个cell运行整段代码
4. sklearn中的Logistic Regression算法：
sklearn是Python实现的开源机器学习算法包，优矿正好也支持它。下面简单介绍下sklearn中Logistic Regression的使用。
4.1 实例化Logistic Regression：
理解什么是正则化，我们先理解正则化的作用： 正则化可防止模型过于复杂。
我们知道机器学习算法本质是一个最优化问题，算法根据训练数据所求得的模型系数可以使得数据分类、拟合等准确率更高。在保证模型准确性的同时，我们同样希望模型不过于复杂，因此我们就要在两者之间权衡。模型的准确性一般用代价函数来衡量，而模型的复杂度一般用系数的平方表示（系数向量的内积）：
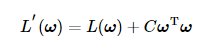在本问题中，我们将极大似然函数的负值视为代价函数，代价函数越小，说明极大似然函数越大，说明模型分类的准确性越高；Cω 用以衡量模型复杂度，C用以控制原代价函数与模型复杂度之间的折中。
很显然，C越大，算法对模型复杂度越敏感。
4.2 训练数据：
其中，train_X 表示的训练数据的特征，其格式n行m列的矩阵，n为训练数据的个数，m为数据的特征个数（维度）；labels 表示的训练数据的类别，格式为n行1列的列向量
4.3 输出模型系数，输出测试数据的类别与概率：
如果用上一节准备好数据，我们可分别得到如下结果：
回归系数： [[-0.55312625 2.2765652 -3.63240141]]
预测类别：输入数据[1.0, 5.0, 2.0]的类别： [ 1.]；输入数据[1.0, 5.0, 4.0]的类别： [ 0.]
预测概率：输入数据[1.0, 5.0, 2.0]为0类1类的概率： [[ 0.04689694 0.95310306]]； 输入数据[1.0, 5.0, 4.0]为0类1类的概率： [[ 0.98597835 0.01402165]]
5. 基于Logistic Regression的简单选股策略：
该策略原理简单，即用T-1天股票的因子值，预测10个交易日后股票的涨跌。训练数据为T-1 到 T-60 之间的滚动时间窗口。策略示意图如下所示：
在回测时，为了避免幸存者偏差，选股都是使用set_universe('HS300', begin_data)，没有直接使用account.universe。
下面的cell给出策略代码及回测结果
