原文You Don’t Know SVD (Singular Value Decomposition)
回想一下高中物理的矢量,例如 力 ,使用矢量表示的力可以被分解到 X 轴和 Y 轴上:
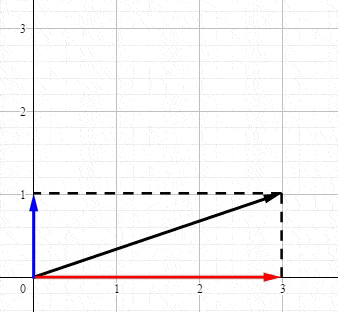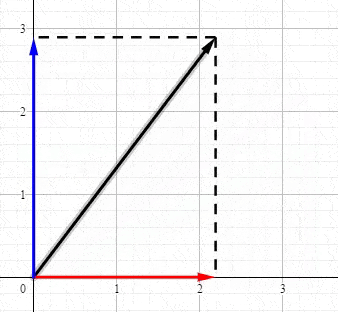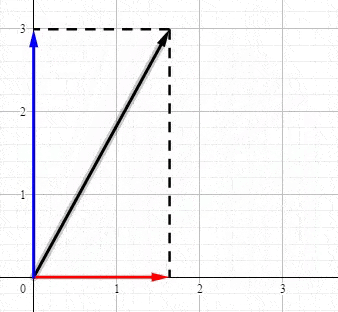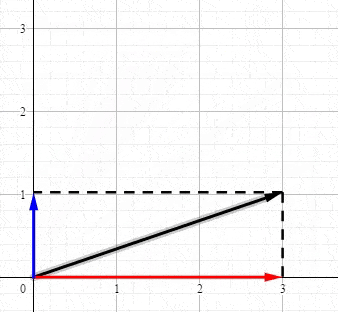
恭喜你。现在你已经知道奇异值分解到底在表达什么了
数学就是给相同概念分配不同名字的艺术,虽然 仅仅就是 SVD 将向量分解到正交的坐标轴上,但我们就想给它一个非常高大上的名字。
我们来看一个例子。
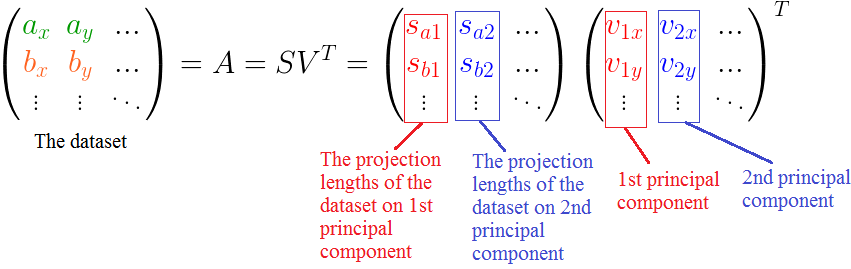
当一个向量 a 被分解,我们可以得到3条重要的信息:
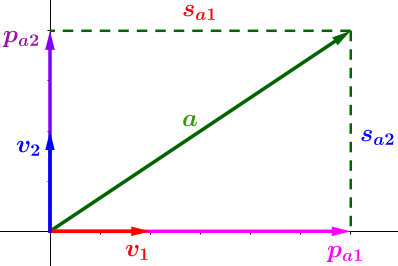
- 投影的 方向 —— 单位向量(V1 和 V2)代表朝哪个方向投影(分解)。在上图中,投影的方向是 X 轴和 Y 轴,另外投影的方向可以是任意的正交方向轴。
- 投影的 长度(线段 Sa1 和 Sa2)—— 这些告诉我们向量在每一个投影的方向上包含了多少(由于 Sa1 > Sa2 ,所以向量 a 在 V1 上 "学习" 到的比在V2 上多)
- 投影 向量 (Pa1 和 Pa2) —— 通过把它们加起来重构原始向量 a (向量的加法)。每一个投影向量都可以用投影方向和投影长度表示: Pa1=Sa1 ***** V1 、Pa2=Sa2 ***** V2 ,因此它们是多余的。
下面给出重要的结论
任何一个向量都可以用:
- 投影方向单位向量(V1,V2 ……)
- 投影在单位方向上的长度( Sa1, Sa2 ……)
表示
SVD所作的一切都是在将这个结论扩展到多个向量(点)和多个维度上:
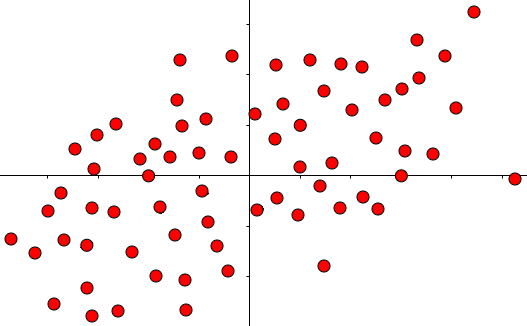
现在,正真的问题是如何如何分解这么多点。
如何分解多个点
要想知道如何分解多个点,就必须知道如何分解一个点!
在数学上,我们通常都会使用矩阵来做这件事。
所以使用矩阵来表示向量分解的操作
这看起来非常自然:
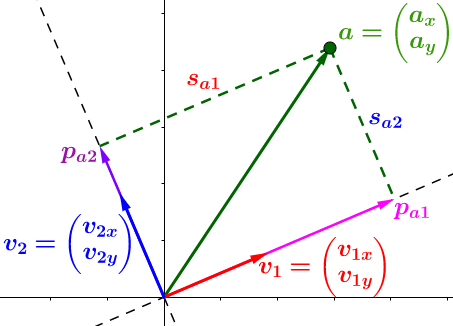
我们想在单位向量V1和V2上分解(投影)向量a。
你可能早就知道了投影是通过 点乘 完成的 —— 它给出了投影的长度(Sa1 和 Sa2):
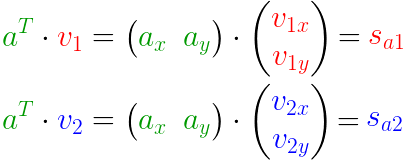
但是这有些冗余。我们可以优化这些矩阵……

我们甚至可以加入更多的点…
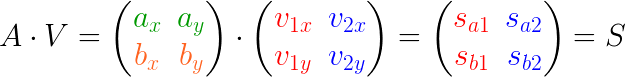
当加入点 b 后,看起来像这样:
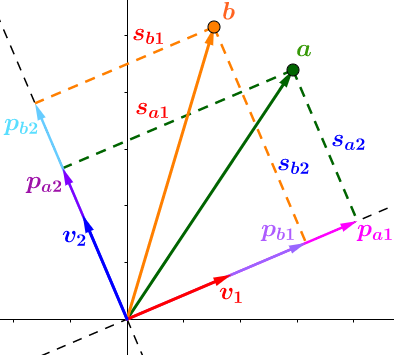
现在就很容易扩展到任意数量的点和任意维度的情况:

这充分体现了数学的优雅。

回顾一下:

完全可以换一个说法:
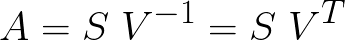
SVD所要表达的全部就是(别忘了前面所提到的重要结论):
任何一组向量 (A) 都可以在某些正交轴 (V) 上以投影长度 (S) 表示。
然而,我们还没有说明白。传统的SVD表达式是这样的:

现在的问题就是要怎么实现:
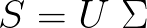
这也正是我们接下来要做的。
如果你稍微仔细一点,你会发现矩阵 S 是像下面这样的组成:
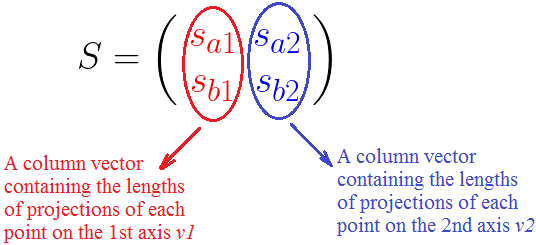
这表明我们最好标准化这些列向量(后面会说原因),例如把它们变成单位长度。
这是通过将每个列向量除以它的大小来实现的,但是是以矩阵的形式来展示。
首先用一个例子看看这个 “除法” 是如何实现的。
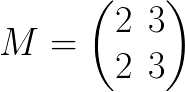
我们想要用 2 除 M 的第一列。为了保持等式,我们必须乘以另一个矩阵:
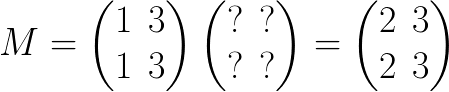
我们可以很直观的想到这个未知的矩阵是一个 第一个元素被除数 2 替换的单位矩阵:

那么第二列除以3就是很直接的了,直接用3替换单位矩阵的第二个元素就可以了:
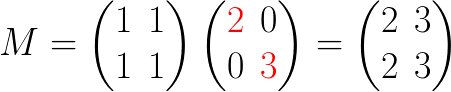
现在我们想把上面的除法应用到矩阵 S。
为了标准化 S 的列,我们除以它们的大小(摸):
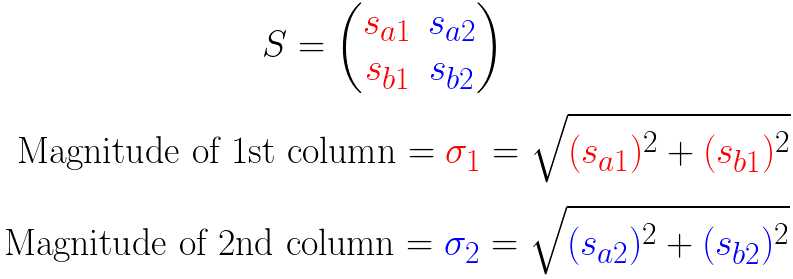
我们对 S 进行和 M 一样的处理:
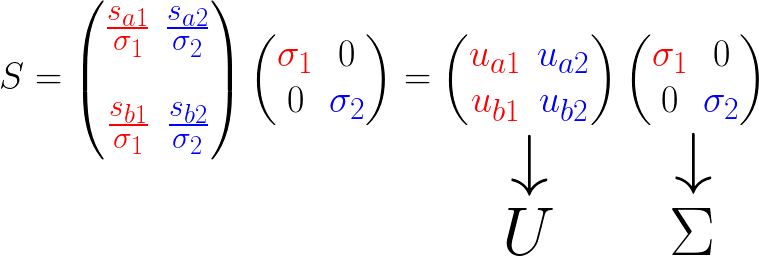
最终
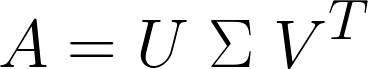
当然,为了不分散对核心概念的注意力,一些精细的细节和严谨的数学都被掩盖了。
解释
我们来讨论一下 U 和 Σ:
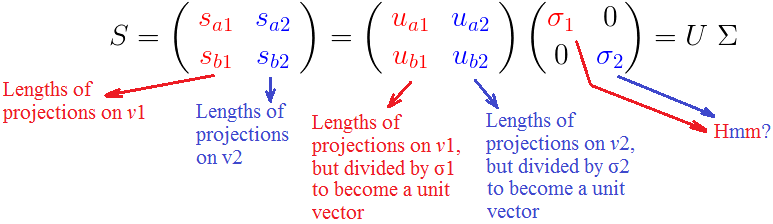
σ是什么?为什么我们要自找麻烦的去标准化 S 来发现它们呢?
我们已经看到(σi)是 所有点,投影在第 i 个单位向量 Vi 上的,投影长度的平方,和,的平方根 。
那这意味着什么呢?
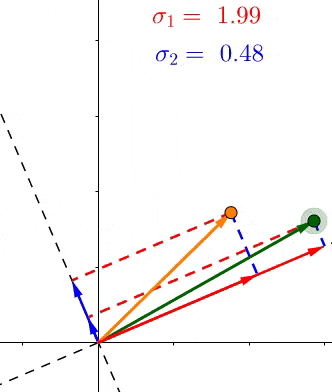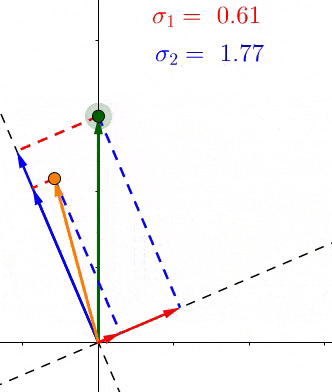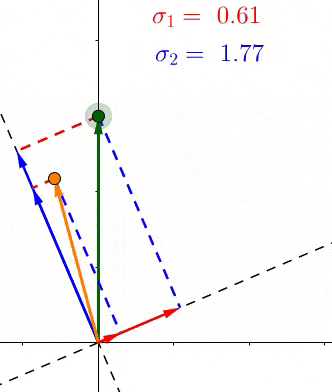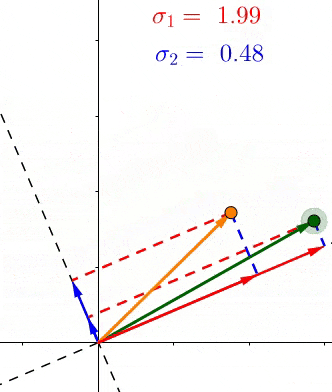
因为根据定义,每个σ都包含了对应的轴上所有点投影长度的和,所以这些σ表示了所有的点有多靠近相应的轴
例如 σ1>σ2 ,那么相对于 V 2 ,大部分的点都更加接近 V 1
这在SVD的无数应用程序中具有巨大的实用价值。
SVD的主要应用
计算矩阵SVD的算法不会乱用投影方向(矩阵V的列)。
它们将这些投影方向作为数据集(矩阵A)的主成分(Principal Components)
这里有一篇关于主成分分析的文章 Dimensionality Reduction For Dummies — Part 1: Intuition(原文作者关于特征降维系列的第一篇,不FQ也可以看,只是加载的慢),直观的解释了PCA中的PC是什么。也可以参考我的翻译主成分分析直观理解。下面是简单的表示:
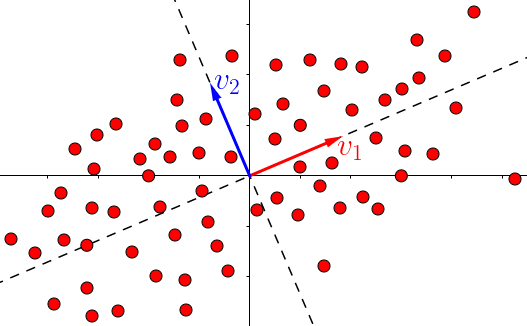
降维的主要目的就是将数据集投影到方差最大的直线(或平面)上:
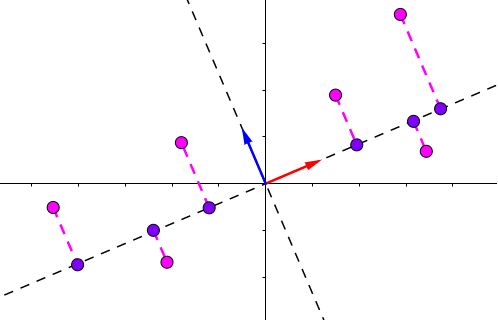
使用SVD使数据集的投影变的很简单,因为所有的点都已经投影在了 所有的主成分上 (单位向量Vi )
例如,将数据集投影到第一个主成分上…
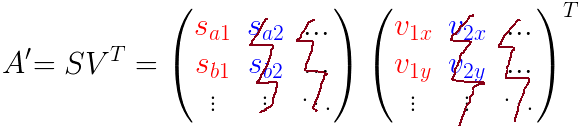
两个矩阵相乘(S 和 VT)得到包含投影点的A'矩阵,如最后一张坐标图所示(紫色的点)