论文笔记(10)"Closing the Gap: Tighter Analysis of Alternating Stochastic Gradient Methods for Bilevel Problems"

Introduction

文章作者针对Bilevel optimization提出了一种对需要采样样本更少的single timescale算法，收敛速度为$\mathcal{O}(\frac{1}{\sqrt{K}})$。

Bilevel optimization问题的通常形式为

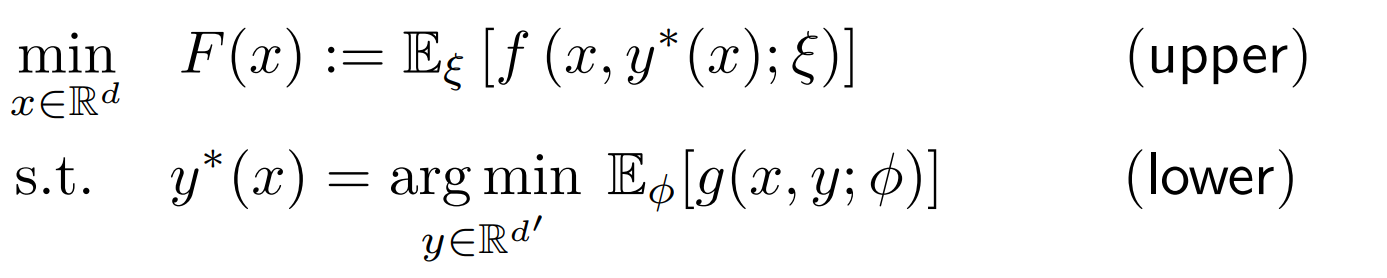
即对于一个嵌套的问题，上层级的问题求解需要子问题的最优解（通常的对偶问题都可以写成这样的形式，如$y$为对偶变量）。

上述问题的求解难点主要在于子问题$y^*(x)$的计算，一般很难得到解析解。

文章主要论题在于当我们用迭代的算法得到一个不精确的$y$时，如何更新$x$以及最终的收敛性、效率如何。

Main Idea

文章的两个主要想法为

$x$的更新方式

\[\begin{align} \nabla F(x)=\nabla_x f(x, y^*(x)) - \nabla_{xy}g(x,y^*(x))[\nabla_{yy} g(x, y^*(x))]^{-1} \nabla_y f(x, y^*(x))\\ \label{eq:gradientx} \end{align} \]
推导过程如下：

\[\begin{align} \nabla F(x) &= \nabla_x f(x, y^*(x)) - \nabla_x y^*(x) \nabla_y f(x, y^*(x))\\ \end{align} \]
对于$\nabla_x y^*(x)$，

\[\begin{align} \nabla_y y^*(x)=0 \end{align} \]
则

\[\begin{align} \underbrace{\nabla_x(\nabla_y y^*(x))}_{\textit{take the gradient w.r.t. x}}&=0\\ \nabla_{xy}y^*(x) + \nabla_xy^*(x)\nabla_{yy}y^*(x)&=0\\ \nabla_{xy}g(x,y^*(x)) + \nabla_xy^*(x)\nabla_{yy} g(x, y^*(x))&=0\\ \end{align} \]
第一个等式是对$\nabla_y y^*(x)$函数对$x$求梯度，要注意$\nabla_x(\nabla_y y^*(x))$和$\nabla_{xy}y^*(x)$的区别。最后得到

\[\begin{align} \nabla_xy^*(x)=-\nabla_{xy}g(x,y^*(x))[\nabla_{yy} g(x, y^*(x))]^{-1} \label{eq:1} \end{align} \]
$y^*(x)$是关于$x$的光滑函数，即

\[\Vert y^*(x_1)-y^*(x_2)\Vert \leq L_y\Vert x_1 -x_2\Vert \]

Algorithm

the update of $y$

通常$y^*$是没有解析解的，文中通过$T$次梯度下降得到在$k$时刻$T$次梯度下降后的结果$y^{k,T}$来替代$y^*(x^{k})$

the update of $x$

将更新后的$y$代替$y^*(x)$带入$\ref{eq:gradientx}$，得到

\[\bar{\nabla}_x f(x,y):=\nabla_x f(x, y) -\nabla_{xy}g(x,y)[\nabla_{yy} g(x, y)]^{-1} \nabla_y f(x, y) \]

其中对于Hessen矩阵的逆，使用近似

\[[\nabla_{yy}g(x,y)]^{-1}\approx [\frac{N}{\ell_{g,1}}\prod_{n=1}^{N'}(I-\frac{1}{\ell_{g,1}}\nabla_{yy}g(x, y;\phi_{(n)}))] \]

其中$\phi_{(n)}$是第$n$个样本点，$N'$是全部$N$个样本中的一部分样本，$\ell_{g,1}$为$\nabla g(x,y)$的Lipschitz continuity值。

这样整个算法流程为

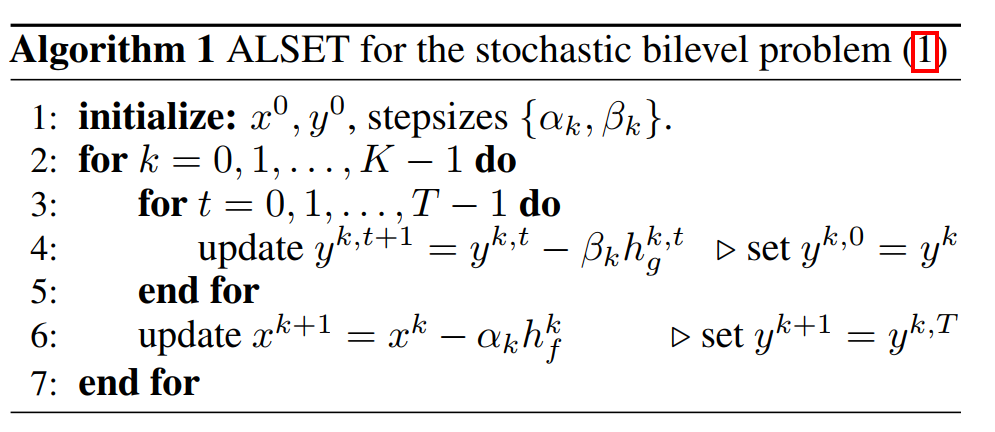
其中

\[\begin{align} h_g^{k,t}&=\nabla_y g(x^{k}, y^{k,t};\phi^{k,t})\\ h_f^{k}&=\nabla_x f(x, y^{k+1};\xi^k)-\nabla_{xy}g(x, y^{k+1};\phi_{(0)})[\frac{N}{\ell_{g,1}}\prod_{n=1}^{N'}(I-\frac{1}{\ell_{g,1}}\nabla_{yy}g(x, y;\phi_{(n)}))]\nabla_y f(x,y^{k+1};\xi) \end{align} \]

Convergence

Assumption

收敛性要求的条件有

$f,\, \nabla f,\, \nabla g,\, \nabla^2g$ 分别是$\ell_{f,0},\, \ell_{f,1},\, \ell_{g,1},\, \ell_{g,2}$Lipschitz continuity
对于任意固定的$x$，$g(x,y)$对于$y$是$\mu_g-$strongly convex
随机梯度$\nabla f(x,y;\xi)$，$\nabla g(x,y;\phi)$和二阶导数$\nabla^2 g(x,y;\phi)$均是无偏的，且方差有界，分别为$\sigma_{f}^2,\, \sigma_{g,1}^2,\,\sigma_{g,2}^2$

Proof

Sketch

令Lyapunov function $\mathbb{V}^{k}:=F(x^{k})+\frac{L_f}{L_y}\Vert y^{k} - y^*(x^k)\Vert$，则

\[\mathbb{V}^{k+1}-\mathbb{V}^{k}=\underbrace{F(x^{k+1})-F(x^{k})}_{\text{upper objective}}+\underbrace{\frac{L_f}{L_y}(\Vert y^{k+1}-y^*(x^{k+1})\Vert-\Vert y(x^k)-y^*(x^k) \Vert)}_{\text{convergence of $y$}} \]

上述的Lyapunov function可以写成两部分，需要证明两者都是下降的。

the convergence of the upper function

先证明$F(x^{k+1})-F(x^k)$是递减，利用$x^{k+1}=x^{k}-\alpha_k h_f^k$得到

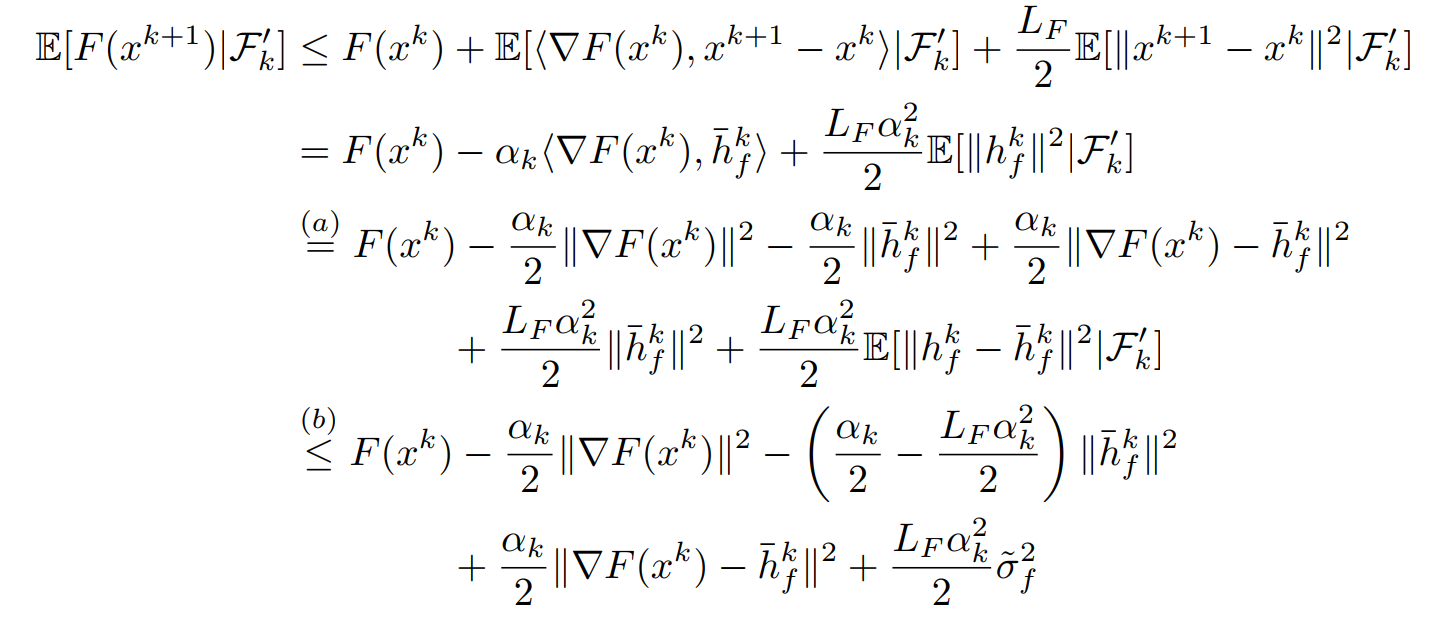
其中$\bar h_f^k$是$h_f^k$的期望，利用$\Vert F(x^k)-\bar h_f^k\Vert = \Vert F(x^k)-h_f^k+h_f^k-\bar h_f^k\Vert$得到

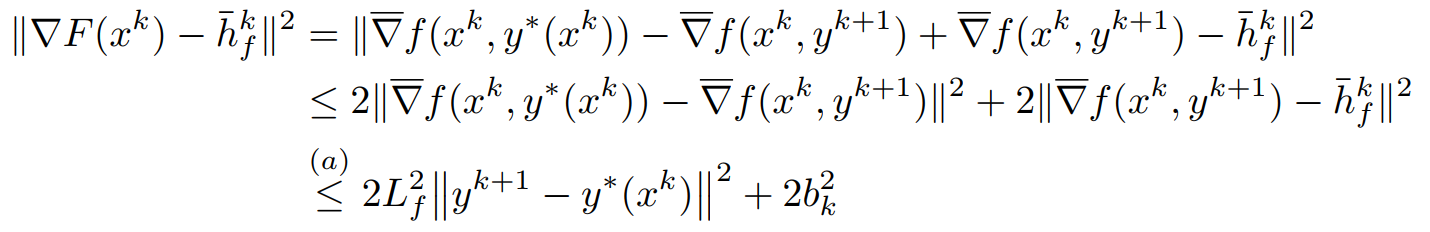
可以看出$F(x^{k+1})-F(x^k)$是依赖于$\Vert y^{k+1}-y^*(x^k)\Vert$的收敛情况的。

the convergence of the lower function

需要注意Lyapunov function中关于$y$的是$\Vert y^k-y^*(x^k)\Vert$，而$y^{k}$在算法中是通过$x^{k-1}$取得的，所以要通过$x$来解耦

\[\Vert y^{k+1} - y^*(x^{k+1})\Vert^2 = \underbrace{\Vert y^{k+1} - y^*(x^{k})\Vert^2}_{J_1} +\underbrace{\Vert y^*(x^{k+1})-y^*(x^{k})\Vert^2}_{J_2}+2\underbrace{\langle y^{k+1}-y^*(x^k),y^*(x^k)-y^*(x^{k+1}) \rangle}_{J_3} \]

这样将原式分为3部分，其中第一部分$J_1$是关于$y^{k+1}$在给定$x^{k}$后是否收敛到$y^*(x^k)$，$J_2$则用到了$y$函数的光滑性。

关于$J_1$这部分是很标准的证明过程

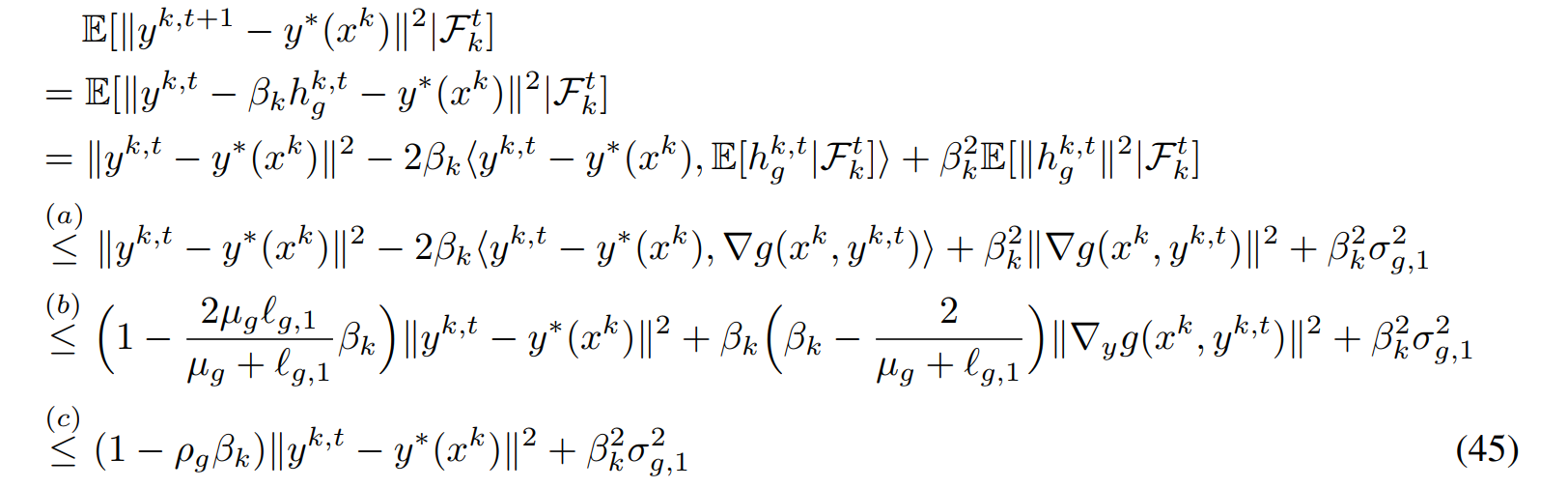
关于$J_2$部分，这里直接使用光滑性质

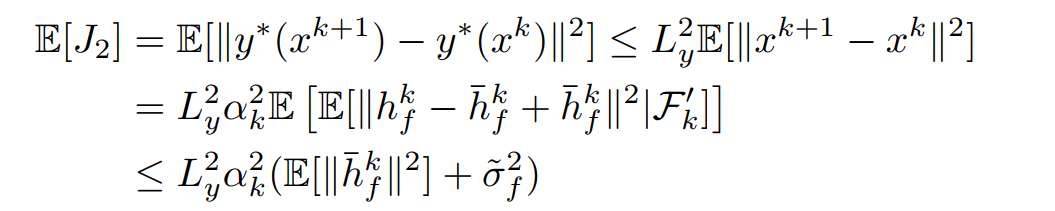
对于$J_3$再次利用$y^*(x)$的光滑性，用$y^*(x^k)-y^*(x^{k+1})-\nabla y^*(x^k)^T(x^{k+1-x^k})+\nabla y^*(x^k)^T(x^{k+1-x^k})$来解耦，得到

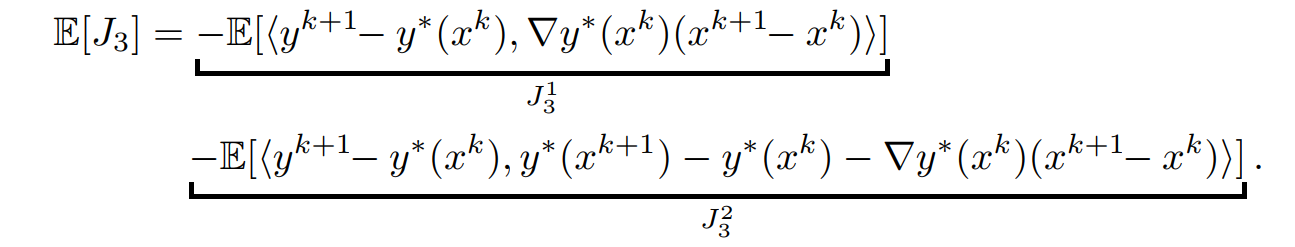
对于$J_3^1$得到

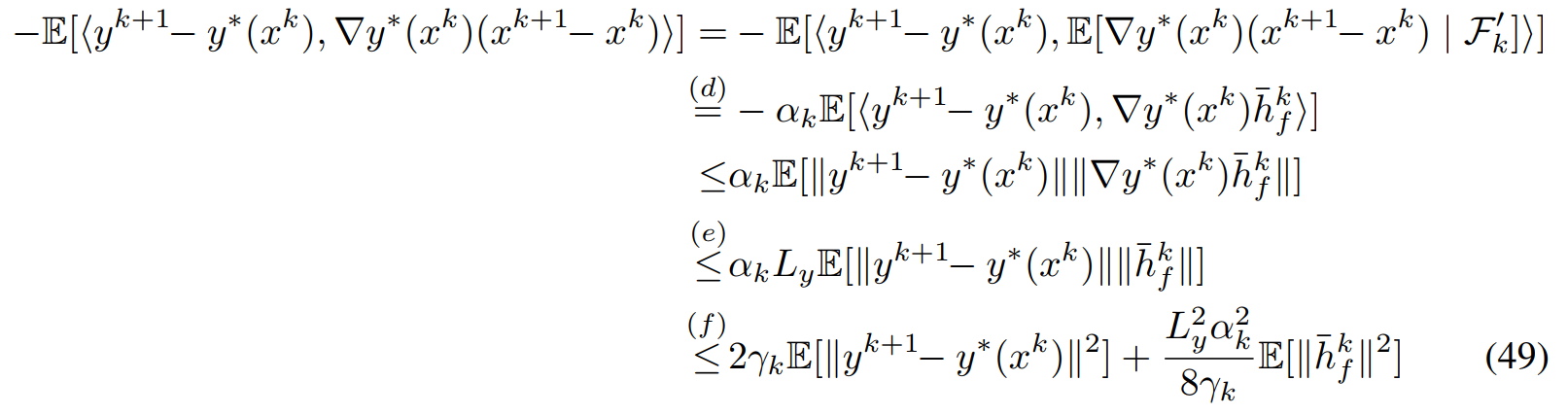
其中最后一个不等式用到了Yong's equality $ab\leq 2\gamma_ka^2+\frac{b^2}{8\gamma_k}$

对于$J_3^2$直接使用光滑性质得到

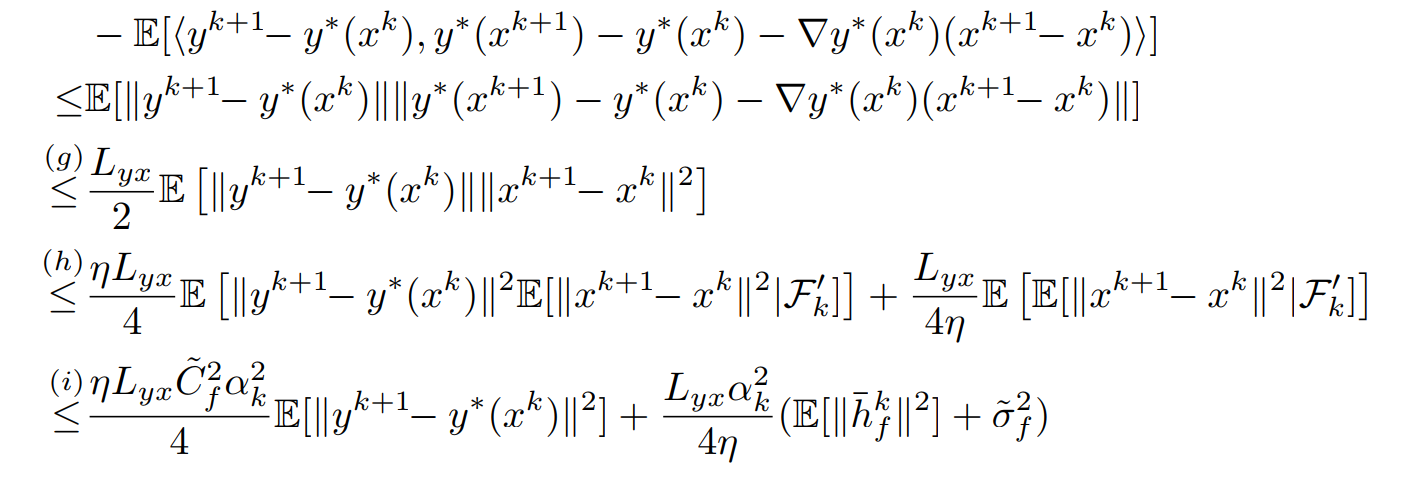
其中$(h)$不等式用到了$1\leq\frac{\eta}{2}+\frac{1}{2\eta}$。最终整合起来得到

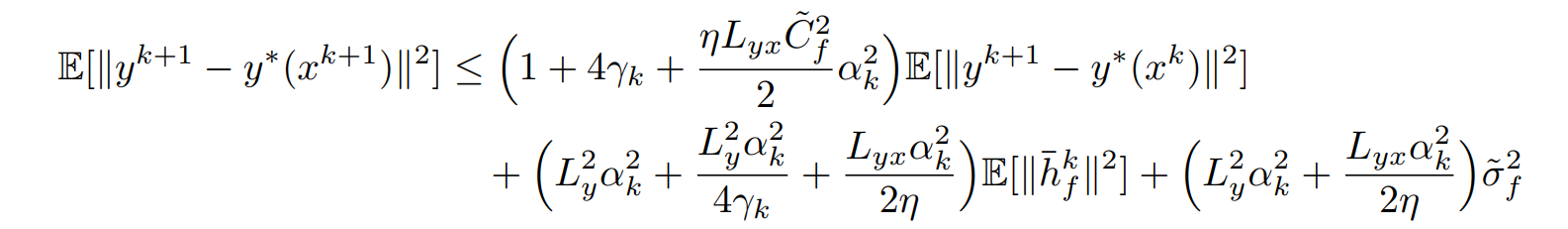
Cases

Min-Max Problems

Min-Max常见于博弈论、优化等领域中，之前的Decomposition，对偶与Proximal都可以归结为这类问题。对于一般的Min-Max问题，其$g(x,y)=-f(x,y)$，因此$\ref{eq:gradientx}$中$\nabla_y f(x,y^*(x))=0$，故更新方式变为

\[\begin{align} h_g^{k,t}&=-\nabla_y f(x^{k}, y^{k,t};\phi^{k,t})\\ h_f^{k}&=\nabla_x f(x^k, y^{k+1};\xi^k) \end{align} \]

Compositional Problems

在Compositional Problems中通常会加入一个norm的正则项，如加入$L_1$-norm的Lasso等问题。对于一般的Compositional problems问题，其$g(x,y)=\Vert y-h(x;\phi)\Vert^2$，$f(x,y):=f(y)$，这样得到新的更新公式为

\[\begin{align} h_g^{k,t}&=y^k-h(x^{k};\phi^k)\\ h_f^{k}&=\nabla h(x^k;\phi^k)\nabla f(y^{k+1};\xi^k) \end{align} \]

Summary

对于$x$更新公式中的$\nabla_{xy}g(x,y^*(x))[\nabla_{yy} g(x, y^*(x))]^{-1}$，我是将其用Newton Methods的方法去理解。
定义的Lyapunov function为upper objective加上一个$R_y=\Vert y^k-y^*(x^k)\Vert$，需要注意的是norm中的$y^*(x^k)$实际上是$k+1$的。
收敛性证明中$F(x)$的收敛性除了和$x$的迭代有关系，还和lower level中$y$的迭代有关系的，需要验证lower level迭代中$y$也是收敛的。
这篇文章很有实践指导意义，例如为什么在Min-Max问题中使用Alternative methods即使不加那个$\nabla_{xy}g(x,y^*(x))[\nabla_{yy} g(x, y^*(x))]^{-1}$也能表现很好？
以及$y^*(x)$确实包含$x$更新方向的信息。