P3373 【模板】线段树 2

题目来源：洛谷

题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1：格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2：格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3：格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入样例#1：

输出样例#1：

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

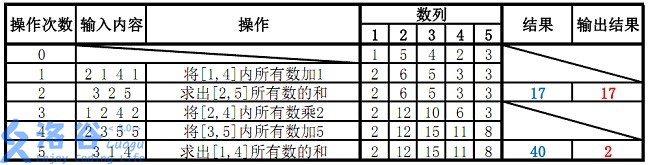
故输出应为17、2（40 mod 38=2）

解析：

这道题难点就在有两种操作，还要分先后顺序。线段树的基本模板就不多说了。

用某高赞题解的话来讲：

面对这两种操作，可以联想到线段树的一个非常好的功能就是lazytag，只计算出确实需要访问的区间的真实值，其他的保存在lazytag里面，这样可以近似O(NlogN)的运行起来。在尝试着写了只有一个lazetag的程序之后我们发现一个lazytag是不能够解决问题的，那就上两个，分别表示乘法意义上的lazytag和加法意义上的lazytag。紧接着想到pushdown操作之后我们又发现必须在向下传递lazytag的时候人为地为这两个lazytag规定一个先后顺序，排列组合一下只有两种情况：

①加法优先，即规定好segtree[root*2].value=((segtree[root*2].value+segtree[root].add)*segtree[root].mul)%p，问题是这样的话非常不容易进行更新操作，假如改变一下add的数值，mul也要联动变成奇奇怪怪的分数小数损失精度，我们内心是很拒绝的；

②乘法优先，即规定好segtree[root*2].value=(segtree[root*2].value*segtree[root].mul+segtree[root].add*(本区间长度))%p，这样的话假如改变add的数值就只改变add，改变mul的时候把add也对应的乘一下就可以了，没有精度损失，看起来很不错。

emmm，我调了很久就对了。

参考代码：

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#define N 100010
#define LL long long
using namespace std;
/*
    码前须知： 
    取余运算对加法，减法，乘法，指数运算皆成立，但对除法不成立：
    (a + b) % p = (a % p + b % p) % p 
    (a - b) % p = (a % p - b % p) % p 
    (a * b) % p = (a % p * b % p) % p 
    a ^ b % p = ((a % p)^b) % p 
    因此，此规律运用得当，本题可以降低相当多的时间复杂度。 
*/
LL a[N],n,m,P;
struct tree{
    LL l,r;
    LL sum,add,multi;
}t[N*4];
void built(LL p,LL l,LL r)
{
    t[p].multi=1;t[p].add=0;
    t[p].l=l;t[p].r=r;
    if(l==r){
        t[p].sum=a[l];
        return;
    }
    LL mid=(l+r)>>1;
    built(p<<1,l,mid);
    built((p<<1)|1,mid+1,r);
    t[p].sum=(t[p<<1].sum+t[(p<<1)|1].sum)%P;
}
void spread(LL p)
{
    //乘法优先原则运算
    t[p<<1].sum=((t[p].multi*t[p<<1].sum)+t[p].add*(t[p<<1].r-t[p<<1].l+1))%P;
    t[(p<<1)|1].sum=((t[p].multi*t[(p<<1)|1].sum)+t[p].add*(t[(p<<1)|1].r-t[(p<<1)|1].l+1))%P;
    //维护线段树,依旧是乘法优先原则 
    t[p<<1].multi=(t[p<<1].multi*t[p].multi)%P;
    t[(p<<1)|1].multi=(t[(p<<1)|1].multi*t[p].multi)%P;
    t[p<<1].add=(t[p].add+t[p<<1].add*t[p].multi)%P;//之前写错，是因为没有深入体会乘法优先 
    t[(p<<1)|1].add=(t[(p<<1)|1].add*t[p].multi+t[p].add)%P;
    //删除延迟标记 
    t[p].add=0;
    t[p].multi=1;
}
LL ask(LL p,LL l,LL r)
{
    if(l<=t[p].l&&t[p].r<=r) return t[p].sum;
    spread(p);
    LL mid=(t[p].l+t[p].r)>>1;
    LL val=0;
    if(l<=mid) val=(val+ask(p<<1,l,r))%P;
    if(r>mid) val=(val+ask((p<<1)|1,l,r))%P;
    return val%P;
}
void change(LL p,LL l,LL r,LL k)
{
    //根据我们规定的乘法优先原则，此处的加法传递函数应先进行乘法运算 
    if(l<=t[p].l&&t[p].r<=r){
        t[p].add=(t[p].add+k)%P;
        t[p].sum=(t[p].sum+k*(t[p].r-t[p].l+1))%P;
        return;
    }
    spread(p);
    LL mid=(t[p].l+t[p].r)>>1;
    if(l<=mid) change(p<<1,l,r,k);
    if(r>mid) change((p<<1)|1,l,r,k);
    t[p].sum=(t[p<<1].sum+t[(p<<1)|1].sum)%P;
}
void multiply(LL p,LL l,LL r,LL k)
{
    if(l<=t[p].l&&t[p].r<=r){
        t[p].sum=(t[p].sum*k)%P;
        t[p].multi=(t[p].multi*k)%P;
        t[p].add=(t[p].add*k)%P;//在某区间的乘法延迟标记乘上某数后，自然的其加法
                                //延迟标记也要乘上去 
        return;
    }
    spread(p);
    LL mid=(t[p].l+t[p].r)>>1;
    if(l<=mid) multiply(p<<1,l,r,k);
    if(r>mid) multiply((p<<1)|1,l,r,k);
    t[p].sum=(t[p<<1].sum+t[(p<<1)|1].sum)%P;
}
int main()
{
    scanf("%lld%lld%lld",&n,&m,&P);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    built(1,1,n);
    while(m--)
    {
        LL l,r,k;
        int flag;
        scanf("%d",&flag);
        if(flag==2){
            scanf("%lld%lld%lld",&l,&r,&k);
            change(1,l,r,k);
        }
        else if(flag==3){
            scanf("%lld%lld",&l,&r);
            printf("%lld
",ask(1,l,r));
        }
        else{
            scanf("%lld%lld%lld",&l,&r,&k);
            multiply(1,l,r,k);
        }
    }
    return 0;
}

2019-05-12 13:39:57