相关博文:
吴恩达机器学习笔记(八) —— 降维与主成分分析法(PCA)
主要内容:
一.向量內积的几何意义
二.基的变换
三.协方差矩阵
四.PCA求解
一.向量內积的几何意义
1.假设A、B为二维平面xoy内两个向量,A为(x1, y1),B为(x2, y2),那么A、B的內积为:AB = |A||B|cosΘ = x1*x2 + y1*y2,结果为一个标量。
2.那么A、B內积的几何意义又是什么呢?单从“|A||B|cosΘ”或者“x1*x2 + y1*y2”这两式子或许还不能发现其中的意义,那么可以在坐标轴上画出这两个向量:

可以看出,|A|cosΘ实际上就是向量A在向量B方向上的投影。假如B为单位向量,即|B| = 1,那么A、B的內积就是A向量在B向量上的投影。
综上:假设B向量为单位向量,那么A、B的內积为:A向量在B向量上的投影,且AB = |A||B|cosΘ = x1*x2 + y1*y2。
二.基的变换
1.基变换,就是用新的正交轴去代替旧的正交轴(原定固定),旧的正交轴就是我们日常所使用的XOY坐标轴,其基向量为 i(1,0) 和 j(0,1)。
注意:基向量必须为单位向量且两两正交(我目前的认知)。
2.例如,有一个向量a在旧坐标轴表示为 (3, 2),我们重新构建一个坐标轴,其基向量分别为 (1/√2,1/√2)和(-1/√2,1/√2)。那么向量a在新坐标轴上表示为 (5/√2,-1/√2)。

3.更一般地:


(注意,新坐标轴的基向量的表示仍然是基于旧坐标轴而言的。)
(2020/2/27补注:
为什么是右乘变换矩阵?而不是右乘?
因为变换矩阵是列向量组成的,每一列都是一个坐标轴。坐标变换的实质是将向量投影到新坐标的每一个坐标轴上,而“投影”就是“内积”,用手比划一下,就知道右乘才是向量与每一个坐标轴的内积了。
)
4.问:为什么新坐标轴的基向量的模要为1且要两两正交?
答:两两正交的单位基向量组成了“标准正交向量组”,将他们按列排成一个矩阵,此矩阵就是“正交矩阵”,同时也可以称为是变换矩阵,即可将向量从旧的坐标轴表示转化为新的坐标轴表示,这个过程就成为“正交变换”,而正交变换不改变向量的內积,从而不改变向量的模、夹角和距离,即不改变形状,而只不过是换了另一种表示。
5.课本上正交矩阵的定义:加入矩阵A满足 A' A = I,则称A为正交矩阵。那么为什么正交矩阵与自身的转置做乘法,会得到一个单位矩阵呢?
答:首先,A'实质上是n个行向量,每一个行向量就是对应的新坐标系的基向量,那么:
1)当这个行向量(在A'上)与自己对应的列向量(在A上)做內积时,结果必定为1(根据內积的几何意义:內积为投影,自己对自己的投影当然就为1了)。
2)当这个行向量(在A'上)与自己别的列向量(在A上)做內积时,结果必定为0,因为这n个向量两两正交,所以內积为0。
综上:只有当“自己与自己”做內积时,结果为1,其他情况为0,所以正交矩阵A满足:A' A = I。
三.协方差矩阵
1.假如我们想重新构建一个能高效表达数据信息的坐标系,所谓“高效”就是信息尽量集中在少数几个或一小部分坐标轴中,而其他坐标轴几乎不含有信息(之后在PCA中就可以去掉这些坐标轴,即减少特征,从而实现降维)。那么怎么衡量坐标轴上信息的多少呢?可以用方差。一般地,在某个坐标轴上,假设数据的方差越大,那么我们可以认为数据在这个坐标轴上所含有的信息量越大。
2.假如,我们想从n维降到k维,那么是不是意味着只需要挑选出前k个方差最大的坐标轴(或者是特征)作为新的坐标系就可以呢?
答:非也!方差最大的轴作为第一维是可以肯定的,但是方差第二大的轴选作第二维却未必。因为方差第二大的轴可能与方差第一大的轴有很强的关联性,转成机器学习的语言就是:两个特征有很强的关联性,这就代表了两个轴之间有很大一部分的信息是重叠了的,即使两者都含有很多信息。对此,能够表示两个不同特征之间关联性的“好汉”是协方差矩阵。
3.协方差矩阵上,对角线表示的是每个特征的方差;而对角线外的表示两个不同特征之间的相关性,大于0时表示两者正相关,小于0则负相关,且绝对值越大,则相关性越强。特别地,当等于0时,表示两特征不相关,即相互独立。(推荐博文以更好地理解协方差矩阵:终于明白协方差的意义了)
4.如何求协方差矩阵?
1)首先对特征进行归一化。为何要归一化?因为特征之间的取值范围的差异可能很大,为了排除这个因素的干扰,需要将它们全都归到一个梯度上去,从而使得方差或者协方差才有可比性。(但我看到《机器学习实战》上的代码没有归一化,不知为何?)
2)假设经过归一化的输入数据为X,协方差矩阵为Σ,那么:

5.得到协方差矩阵,即知道了每两两特征之间的相关性,那这对于选取k个信息最大的特征又有和帮助呢?请看下回(节)分解。
四.PCA求解
1.假设归一化后的输入数据X的协方差矩阵为Cx,为了能够更加高效地表示数据,我们重新构造出一个坐标系(基向量仍然为n个,后面再挑选出最好的k个),假设这个坐标系的基向量所构成的矩阵为P(n个列向量),可知P为正交矩阵(在手写的那一大段文字有解释)。接下来将X从原来的坐标系转换到新的坐标系,那么新的坐标表示为:Y = X*P。
2.假设Y的协方差矩阵为Cy,那么我们的目标就是:求出这个正交变换P(也就是求出这个新的坐标系),使得协方差矩阵Cy上除了对角线之外的其他元素都为0(这里可以看出是线代里面的实对称矩阵的正交对角化了),从而使得每两两特征之间都互不相关,于是就可以单凭数据在特征上的方差选出含信息量最大的那k个特征(根据线代的知识可知,对角矩阵的第i个数对应正交变化P的第i列,P的列是正交基。)
3.有了目标之后,就尝试从公式下手:
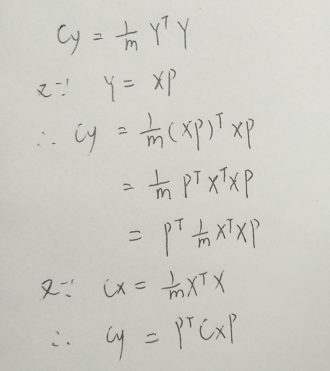
4.从形式上看,不就是要我们对Cx对角化吗?更准确地:因为Cx为是实对称矩阵,所以必定有正交矩阵P满足条件(定理来的,线代第五章,先是讲普通矩阵的对角化,再讲实对称矩阵的正交对角化)。
至于对角化,我们只需要求出Cx的特征向量,就可以组合成正交矩阵P了。而这些特征向量,就是我们重新构建出来的那n个在新坐标系上的坐标轴,即新特征。
5.那么又怎么从中挑选出含信息量最大的k个坐标轴呢?
答:这就要回看协方差矩阵Cy,它是一个对角矩阵,对角线上的元素就是Cy的特征值,更重要的是:他们就是在新坐标系上每个坐标轴(应该叫做特征比较合适)的方差,那么只需对这些方差排个序,选出前k个特征值对应的特征向量,以此组成新的维度更少的坐标系、组成新的更少的特征,从而实现降维,这就是PCA。