CF446C题意:
给你一个数列(a_i),有两种操作:区间求和;(sum_{i=l}^{r}(a[i]+=fib[i-l+1]))。(fib)是斐波那契数列。
思路
(一)
codeforces 447E or 446C
(fib[n] = frac{sqrt5}{5} imes [(frac{1+sqrt5}{2})^n-(frac{1-sqrt5}{2})^n])
有关取模、同余、逆元的一些东西:
(p = 1e9 + 9)
(383008016^2 ≡ 5 (mod;p))
(383008016 ≡ sqrt5 (mod;p))
(frac{1}{sqrt5}≡276601605(mod;p))
(383008016的逆元 = 276601605)
((1+sqrt5)/2≡691504013(mod;p))
(383008017 imes 2的逆元 = 691504013)
((1-sqrt5)/2≡308495997(mod;p))
((p-383008016+1) imes 2的逆元 = 308495997)
(fib[n] = 276601605 imes [(691504013)^n-(308495997)^n] (mod;;p))
等比数列求和:(sum = frac{a}{a-1} imes (a^n - 1) (mod;;p) = a^2(a^n-1)(mod;;p)=a^{n+2}-a^2(mod;;p))
当(p=1e9+9, a = 691504013或308495997时成立)。
所以本题我们只需要用线段树lazy标记维护两个等比数列第一项为一次项的系数即可。代码如下。
#include<bits/stdc++.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;
const int MXN = 5e5 + 6;
const int INF = 0x3f3f3f3f;
const LL mod = 1000000009;
const LL p1 = 691504013;
const LL p2 = 308495997;
const LL p3 = 276601605;
int n, m;
LL ar[MXN], pre[MXN], mul1[MXN], mul2[MXN];
LL sum[MXN<<2], lazy1[MXN<<2], lazy2[MXN<<2];
LL ksm(LL a, LL b) {
LL res = 1;
for(;b;b>>=1,a=a*a%mod) {
if(b&1) res = res * a %mod;
}
return res;
}
void check(LL &a) {
if(a >= mod) a %= mod;
}
void push_up(int rt) {
sum[rt] = sum[lson] + sum[rson]; check(sum[rt]);
}
void push_down(int l,int r,int rt) {
if(lazy1[rt] == 0 && lazy2[rt] == 0) return;
LL a = lazy1[rt], b = lazy2[rt];
int mid = (l + r) >> 1;
int len1 = mid-l+1, len2 = r - mid;
lazy1[lson] += a; lazy2[lson] += b;
sum[lson] = sum[lson] + a*((mul1[len1+2]-mul1[2])%mod+mod); check(sum[lson]);
sum[lson] = (sum[lson] - b*((mul2[len1+2]-mul2[2])%mod+mod))%mod + mod; check(sum[lson]);
lazy1[rson] += a*mul1[len1]%mod; lazy2[rson] += b*mul2[len1]%mod;
sum[rson] = sum[rson] + a*mul1[len1]%mod*((mul1[len2+2]-mul1[2])%mod+mod); check(sum[rson]);
sum[rson] = (sum[rson] - b*mul2[len1]%mod*((mul2[len2+2]-mul2[2])%mod+mod))%mod + mod; check(sum[rson]);
lazy1[rt] = lazy2[rt] = 0;
check(lazy1[lson]);check(lazy1[rson]);check(lazy2[lson]);check(lazy2[rson]);
}
void update(int L,int R,int l,int r,int rt,LL x,LL y) {
if(L <= l && r <= R) {
lazy1[rt] += x; lazy2[rt] += y;
check(lazy1[rt]); check(lazy2[rt]);
sum[rt] = sum[rt] + x*((mul1[r-l+3]-mul1[2])%mod+mod); check(sum[rt]);
sum[rt] = (sum[rt] - y*((mul2[r-l+3]-mul2[2])%mod+mod))%mod + mod; check(sum[rt]);
return;
}
push_down(l, r, rt);
int mid = (l + r) >> 1;
if(L > mid) update(L,R,mid+1,r,rson,x,y);
else if(R <= mid) update(L,R,l,mid,lson,x,y);
else {
update(L,mid,l,mid,lson,x,y);
update(mid+1,R,mid+1,r,rson,mul1[mid-L+1]*x%mod,mul2[mid-L+1]*y%mod);
}
push_up(rt);
}
LL query(int L,int R,int l,int r,int rt) {
if(L <= l && r <= R) {
return sum[rt];
}
push_down(l,r,rt);
int mid = (l+r) >> 1;
if(L > mid) return query(L,R,mid+1,r,rson);
else if(R <= mid) return query(L,R,l,mid,lson);
else {
LL ans = query(L,mid,l,mid,lson);
ans += query(mid+1,R,mid+1,r,rson);
check(ans);
return ans;
}
}
int main() {
//printf("%d
", ksm(691504013-1,mod-2));
//printf("%d
", ksm(308495997-1,mod-2));
//F(n) = √5/5[((1+√5)/2)^n-((1-√5)/2)^n]
//383008016^2 ≡ 5 (mod 1e9 + 9)
//383008016 ≡ sqrt(5) (mod 1e9 + 9)
//printf("%lld
", ksm(383008016,mod-2));//1/sqrt(5)≡276601605(mod)
//printf("%lld
", 383008017*ksm(2,mod-2)%mod);//(1+sqrt(5))/2≡691504013(mod)
//printf("%lld
", (mod-383008016+1)*ksm(2,mod-2)%mod);//(1-sqrt(5))/2≡308495997(mod)
scanf("%d%d", &n, &m);
mul1[0] = mul2[0] = 1;
for(int i = 1; i < 301000; ++i) {
mul1[i] = mul1[i-1] * p1;
mul2[i] = mul2[i-1] * p2;
check(mul1[i]); check(mul2[i]);
}
for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]), pre[i] = (pre[i-1] + ar[i])%mod;
while(m --) {
int opt, l, r;
scanf("%d%d%d", &opt, &l, &r);
if(opt == 1) {
update(l, r, 1, n, 1, 1, 1);
}else {
printf("%lld
", ((p3*query(l,r,1,n,1)%mod+pre[r]-pre[l-1])%mod+mod)%mod);
}
}
return 0;
}
(二)
斐波纳契数列的一些性质:
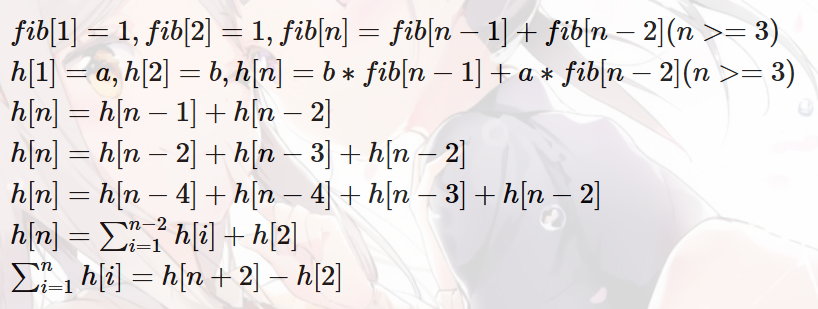
性质1:对于一个满足斐波那契性质的数列,如果我们已知它的前两项,我们可以O(1)的得到它的任意一项和任意前缀和!
性质2:两个满足斐波那契性质的数列相加后,依然是斐波那契数列。前两项的值分别为两个的和。
所以本题我们用线段树的(lazy)标记维护给这个区间各项加上的(fib)数列的前两项的值。通过这个(lazy)标记我们可以(O(1))更新区间和,因为斐波纳契数列满足可加性,所以我们(lazy)标记也可以很轻松的(push\_down)操作。代码如下。
#include<bits/stdc++.h>
#define lson rt<<1
#define rson rt<<1|1
using namespace std;
typedef long long LL;
const int MXN = 5e5 + 6;
const int INF = 0x3f3f3f3f;
const LL mod = 1000000009;
const LL p1 = 691504013;
const LL p2 = 308495997;
const LL p3 = 276601605;
int n, m;
LL ar[MXN], fib[MXN];
LL sum[MXN<<2], lazy1[MXN<<2], lazy2[MXN<<2];
LL ksm(LL a, LL b) {
LL res = 1;
for(;b;b>>=1,a=a*a%mod) {
if(b&1) res = res * a %mod;
}
return res;
}
LL hn(int n,LL a,LL b) {
if(n == 1) return (a%mod+mod)%mod;
if(n == 2) return (b%mod+mod)%mod;
return ((a*fib[n-2] + b*fib[n-1])%mod+mod)%mod;
}
void check(LL &a) {
if(a >= mod) a %= mod;
}
void push_up(int rt) {
sum[rt] = sum[lson] + sum[rson]; check(sum[rt]);
}
void build(int l,int r,int rt) {
if(l == r) {
sum[rt] = ar[l];
return;
}
int mid = (l + r) >> 1;
build(l, mid, lson); build(mid+1, r, rson);
push_up(rt);
}
void push_down(int l,int r,int rt) {
if(lazy1[rt] == 0 && lazy2[rt] == 0) return;
LL a = lazy1[rt], b = lazy2[rt];
int mid = (l + r) >> 1;
int len1 = mid-l+1, len2 = r - mid;
lazy1[lson] += a; lazy2[lson] += b;
sum[lson] = (sum[lson] + hn(len1+2,a,b) - b)%mod+mod;
lazy1[rson] += hn(len1+1,a,b); lazy2[rson] += hn(len1+2,a,b);
sum[rson] = (sum[rson] + hn(len2+2,hn(len1+1,a,b),hn(len1+2,a,b))-hn(len1+2,a,b))%mod+mod;
check(sum[lson]); check(sum[rson]);
check(lazy1[lson]);check(lazy1[rson]);check(lazy2[lson]);check(lazy2[rson]);
lazy1[rt] = lazy2[rt] = 0;
}
void update(int L,int R,int l,int r,int rt,LL x, LL y) {
if(L <= l && r <= R) {
lazy1[rt] += x; lazy2[rt] += y;
check(lazy1[rt]); check(lazy2[rt]);
sum[rt] = (sum[rt] + hn(r-l+1+2,x,y) - y)%mod+mod; check(sum[rt]);
return;
}
push_down(l, r, rt);
int mid = (l + r) >> 1;
if(L > mid) update(L,R,mid+1,r,rson,x,y);
else if(R <= mid) update(L,R,l,mid,lson,x,y);
else {
update(L,mid,l,mid,lson,x,y);
update(mid+1,R,mid+1,r,rson,hn(mid-L+1+1,x,y), hn(mid-L+1+2,x,y));
}
push_up(rt);
}
LL query(int L,int R,int l,int r,int rt) {
if(L <= l && r <= R) {
return sum[rt];
}
push_down(l,r,rt);
int mid = (l+r) >> 1;
if(L > mid) return query(L,R,mid+1,r,rson);
else if(R <= mid) return query(L,R,l,mid,lson);
else {
LL ans = query(L,mid,l,mid,lson);
ans += query(mid+1,R,mid+1,r,rson);
check(ans);
return ans;
}
}
int main() {
scanf("%d%d", &n, &m);
fib[1] = fib[2] = 1;
for(int i = 3; i < 301000; ++i) {
fib[i] = fib[i-1] + fib[i-2];
check(fib[i]);
}
for(int i = 1; i <= n; ++i) scanf("%lld", &ar[i]);
build(1, n, 1);
while(m --) {
int opt, l, r;
scanf("%d%d%d", &opt, &l, &r);
if(opt == 1) {
update(l, r, 1, n, 1, 1, 1);
}else {
printf("%lld
", query(l,r,1,n,1));
}
}
return 0;
}