又一道没有做出来的题
首先做最基础的mobius反演,可以得到,答案就是一堆fi^k乘起来,k是下面这个东西。
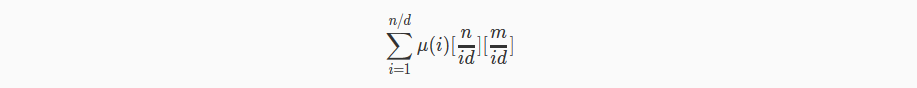
套路的用T代替id,并枚举T。
指数的式子变成 π(i|T) mu(T/i)✖(n/T)✖(m/T)
考虑先枚举指数再枚举i(没想到这一步!)
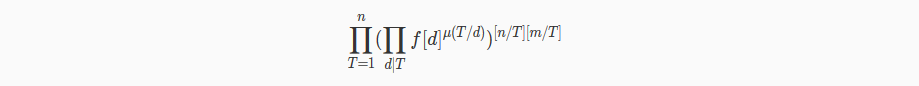
令dp[T]=π (i|T) f[i]^mu(T/i)。
dp[T]可以在一个调和级数的复杂度内求出。
求出dp数组的前缀积,就可以除法分块sqrt(n)logn解决本题。
#include<bits/stdc++.h>
#define N 2200000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline int read()
{
char ch=0;
int x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
const int mo=1e9+7;
bool is_prime[N];
int f[N],mu[N],prime[N];
void solve(int n)
{
memset(is_prime,true,sizeof(is_prime));
is_prime[0]=is_prime[1]=false;
mu[0]=mu[1]=1;f[0]=0;f[1]=1;
for(int i=2,cnt=0;i<=n;i++)
{
f[i]=(f[i-1]+f[i-2])%mo;
if(is_prime[i])mu[i]=-1,prime[++cnt]=i;
for(int j=1;j<=cnt;j++)
{
int k=i*prime[j];
if(k>n)break;
is_prime[k]=false;
if(i%prime[j])mu[k]=-mu[i];else {mu[k]=0;break;}
}
}
}
int t,len,dp[N],pd[N];
int ksm(int x,int k)
{
int ans=1;
while(k)
{
if(k&1)ans=1ll*ans*x%mo;
k>>=1;x=1ll*x*x%mo;
}
return ans;
}
void work()
{
int n=read(),m=read(),ans=1;
for(int l=1,r;l<=min(n,m);l=r+1)
{
r=min(n/(n/l),m/(m/l));
ans=1ll*ans*ksm(1ll*dp[r]*pd[l-1]%mo,1ll*(n/l)*(m/l)%(mo-1))%mo;
}
printf("%d
",(ans%mo+mo)%mo);
}
int main()
{
t=read();len=1e6;solve(len);
for(int i=0;i<=len;i++)dp[i]=pd[i]=1;
for(int i=1;i<=len;i++)
{
int x=f[i],y=ksm(f[i],mo-2);
for(int j=i;j<=len;j+=i)
{
if(mu[j/i]==+1)dp[j]=1ll*dp[j]*x%mo,pd[j]=1ll*pd[j]*y%mo;
if(mu[j/i]==-1)dp[j]=1ll*dp[j]*y%mo,pd[j]=1ll*pd[j]*x%mo;
}
}
for(int i=1;i<=len;i++)dp[i]=1ll*dp[i]*dp[i-1]%mo,pd[i]=1ll*pd[i]*pd[i-1]%mo;
for(int i=1;i<=t;i++)work();
return 0;
}