A.Find Divisible
沙比题
显然l和2*l可以直接满足条件。
代码
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 110000
#define L 100000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
char ch=0;
ll x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
int main()
{
ll t=read();
for(ll i=1;i<=t;i++)
{
ll l=read(),r=read();
cout<<l<<" "<<2*l<<endl;
}
return 0;
}
B.Substring Removal
细节题
分类讨论一下
先看一下是否整个字符串为同一种字符,此时答案为子串个数,特判掉。
如果不满足,则求出最长的前、后缀满足字符相等。
分别设为a,b。
ans=1+a+b+a*b(1为删除整个串的情况)
代码
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 1100000
#define L 1000000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
char ch=0;
ll x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
const ll mo=998244353;
char s[N];
int main()
{
ll n=read(),a=0,b=0,ans=1;
scanf("%s",s+1);if(n==1){printf("1");return 0;}
a=1;while(a<n&&s[a]==s[a+1])a++;ans+=a;
b=n;while(b>1&&s[b]==s[b-1])b--;ans+=n-b+1;
if(a==n&&b==1){cout<<(((n*(n-1)/2))%mo);return 0;}
if(s[1]==s[n])
{
ans=(ans+((a*(n-b+1))%mo))%mo;
cout<<ans%mo;
return 0;
}
else
{
cout<<ans%mo;
return 0;
}
return 0;
}
C.Polygon for the Angle
数论题
首先可以发现
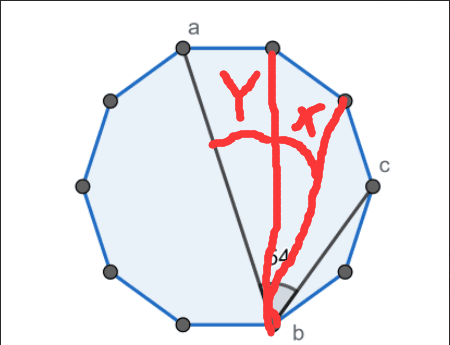
类似x和y这样的角是相等的。(可以构造外接圆,然后利用等弦对等角证明)
考虑计算这种角的大小
(n-2)*180/n是一个内角的大小,再除以n-2即为这种角的大小。
显然,n边形合法的条件是n/180|ang
当然可以直接数论强推。
这里讲一个简单的做法。
就是直接枚举n,强行判断一下即可。
需要注意的是,即使满足了整除这个条件,仍然有可能不合法。
比如第四个样例
query:178
answer:180
答案不是90的原因是90边形虽然满足了整除这个条件,但是最大的角也只有176°。
注意一下这个问题即可。
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 110000
#define L 100000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
char ch=0;
ll x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
int main()
{
ll t=read();
for(ll o=1;o<=t;o++)
{
ll ang=read();
bool flag=false;
for(ll i=1;i<=400;i++)
{
ldb x=180.0/(ldb)i,k=(ldb)ang/x;
if((180.0-x*2.0>=(ldb)ang)&&(fabs(k-(ll)k)<=0.0001||fabs(k-(ll)k)>=0.9999))
{
cout<<i<<endl;
flag=true;break;
}
}
if(!flag)printf("-1
");
}
return 0;
}
D.Easy Problem
垃圾dp题
直接dp[i][j]表示放了i个数匹配hard匹配到了第j位。
每次决策有两种。
删除:代价ai,强制j保持不变。
不删除:无代价,j根据s[i]是否和j+1匹配来决定是否+1。
代码
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 150000
#define L 100000
#define eps 1e-7
#define inf 1e18+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
char ch=0;
ll x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
ll n,a[N],dp[N][5];
char s[N],ch[5]={'0','h','a','r','d'};
ll dfs(ll x,ll k)
{
if(x==n+1)return 0;
if(dp[x][k]!=-1)return dp[x][k];
dp[x][k]=inf;
if(s[x]==ch[k+1])
{
if(k!=3)dp[x][k]=min(dp[x][k],dfs(x+1,k+1));
}
else dp[x][k]=min(dp[x][k],dfs(x+1,k));
dp[x][k]=min(dp[x][k],dfs(x+1,k)+a[x]);
return dp[x][k];
}
int main()
{
n=read();scanf("%s",s+1);
for(ll i=1;i<=n;i++)a[i]=read();
memset(dp,-1,sizeof(dp));
cout<<dfs(1,0);
return 0;
}
E.The Top Scorer
组合,容斥,概率。
考虑枚举最大值和最大值的个数,分别设为o,i。
发现满足这个条件的方案数=c(n,i)f(n-i,s-io,o)
f(i,j,k)函数的意义是把和为j的数字分配给i个人,每个人的数字严格<k的方案数。
这个也就等价于sigema xi=j (xi<k)的解的个数。
这是一个经典的容斥题。
容斥的大体思路就是枚举至少有几个人的数值>=k(即不合法的个数)
用插板法去计算。
计算的复杂度为O(n)(n为人数个数)
考虑计算出来的方案数,对于有i个最大值的情况,每一种方案都有1/i的概率是第一个人获胜。
对总概率的贡献需要乘上一个1/i。
最终再除以一下总方案数即可(插板法计算)
代码
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 220000
#define L 200000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
char ch=0;
ll x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
const ll mo=998244353;
ll ksm(ll x,ll k)
{
ll ans=1;
while(k)
{
if(k&1)ans=(ans*x)%mo;
k>>=1;
x=(x*x)%mo;
}
return ans;
}
ll fac[N],vac[N];
ll inv(ll x){return ksm(x,mo-2);}
ll c(ll n,ll m){return (fac[n]*((vac[m]*vac[n-m])%mo))%mo;}
int main()
{
ll n=read(),s=read(),r=read(),ans=0;
if(n==1){printf("1");return 0;}
fac[0]=vac[0]=1;for(ll i=1;i<=L;i++)fac[i]=(fac[i-1]*i)%mo,vac[i]=(vac[i-1]*inv(i))%mo;
for(ll o=r;o<=s;o++)for(ll i=1;i<=n&&i*o<=s;i++)
{
ll m=n-i,v=s-i*o,x=0;
for(ll k=0,flag=1;k<=m&&v-k*o>=0;k++,flag=-flag)
x=(x+flag*c(m,k)*c(v-k*o+m-1,m-1))%mo;
if(!m&&!v)x=1;
ans=(ans+((inv(i)*((c(n-1,i-1)*x)%mo))%mo))%mo;
}
ans=(ans*inv(c(s-r+n-1,n-1)))%mo;
cout<<ans;
return 0;
}
F.Inversion Expectation
概率,期望。
根据期望是线性函数这一性质,拆开算。
已知和已知的逆序对。
未知和未知的逆序对。
已知和未知的逆序对。
前两个都是非常好计算的。
计算第三个的时候。
考虑每一个已知的数字x。
设它左边有a个数未知,右边有b个数未知
再设共有k个比它小的数字未知。
显然这k个数相对x来说应该等概率分布。
左边期望有ka/(a+b)个,右边有kb/(a+b)个。
算一下即可。
G.Lucky Tickets
多项式模板题
发现题意就是让你先算出长度为n/2,和为k,(k<=n/2✖10)的方案数。
然后再乘法原理搞一搞。
考虑怎么计算和为k的方案数。
考虑暴力dp,用分治实现。
dp[n][k]=sigema dp[n/2][i]*dp[n/2][k-i]
(如果n为奇数,还需要再卷上一个dp[1])
显然这是一个卷积的形式。
进一步的,发现这是一个多项式幂的形式。
直接分治+ntt即可。
代码
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#define N 4400000
#define L 4000000
#define eps 1e-7
#define inf 1e9+7
#define ll long long
using namespace std;
inline int read()
{
char ch=0;
int x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
const ll d=3,mo=998244353;
ll ksm(ll x,ll k)
{
ll ans=1;
while(k)
{
if(k&1)ans=(ans*x)%mo;
k>>=1;
x=(x*x)%mo;
}
return ans;
}
int rev[N];
void ntt(ll *f,int n,int flag)
{
ll t,w,wn;
int i,j,k,kk;
for(i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)+((i&1)*(n>>1));
for(i=0;i<n;i++)if(i<rev[i])swap(f[i],f[rev[i]]);
for(k=2,kk=1;k<=n;k<<=1,kk<<=1)
{
wn=ksm(d,(mo-1)/k);
if(flag==-1)wn=ksm(wn,mo-2);
for(i=0;i<n;i+=k)
for(j=0,w=1;j<kk;j++,w=(w*wn)%mo)
{
t=(w*f[i+j+kk])%mo;
f[i+j+kk]=(f[i+j]-t+mo)%mo;
f[i+j]=(f[i+j]+t)%mo;
}
}
if(flag==-1)
{
ll inv=ksm(n,mo-2);
for(int i=0;i<n;i++)f[i]=(f[i]*inv)%mo;
}
}
ll a[N],b[N],f[N],g[N];
void solve(int n)
{
if(n==1)return;
solve(n/2);
int len;
for(len=1;len<=n*10;len<<=1);for(int i=0;i<len;i++)a[i]=f[i];
ntt(a,len,+1);for(int i=0;i<len;i++)a[i]=(a[i]*a[i])%mo;ntt(a,len,-1);
for(int i=0;i<len;i++)f[i]=a[i];
if(n&1)
{
for(len=1;len<=n*10;len<<=1);
for(int i=0;i<len;i++)a[i]=f[i],b[i]=g[i];
ntt(a,len,+1);ntt(b,len,+1);
for(int i=0;i<len;i++)a[i]=(a[i]*b[i])%mo;
ntt(a,len,-1);
for(int i=0;i<len;i++)f[i]=a[i];
}
}
int main()
{
int n=read()/2,k=read(),x;
for(int i=1;i<=k;i++)x=read(),f[x]=g[x]=1;
solve(n);
ll ans=0;
for(int i=0;i<=n*10;i++)ans=(ans+((f[i]*f[i])%mo))%mo;
cout<<ans;
return 0;
}