数据结构与算法分析

1.树

描述：自由树是一个连通的，无回路的无向图。

树不是一种线性结构，但它具有一定的线性特征。

树也可以这样定义：树是由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或称为树根。

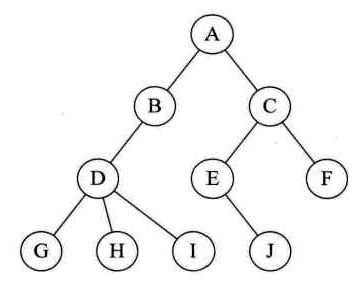
2.树的属性

节点的深度：约定根节点的深度为0，每个节点的深度为该节点到根节点的唯一通路所经过的边的数目。

节点的层次：相同深度的节点属于同一层次。

节点的度（数）：节点的孩子总数。

子树：某节点所有后代及其联边称作子树。

高度：一棵树所有节点中深度的最大值即为高度，单个节点的树高度为0，空树高度为-1

叶节点：没有子节点的节点为叶节点，树中必存在叶节点。

3.二叉树

树的种类非常多，二叉树是树的一个特例，尽管作为一个特例，二叉树也具有自身的一般性。

描述：二叉树是一棵树，其中每个节点都不能有多于两个的儿子。

因为同一个父节点下最多有两个子节点，所以也可以用左右区分二叉树的左右子节点。

真二叉树：不含一度节点的二叉树（可以不含节点）

满二叉树：一棵深度为k，且有2^k-1个节点的树是满二叉树。

完全二叉树：对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

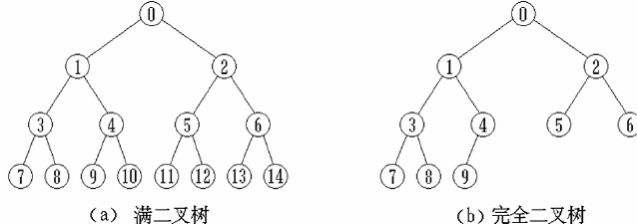
如上图，完全二叉树中的每一个节点都可以对应到相同深度的满二叉树上。

满二叉树一定是完全二叉树，反之则不然。

4.二叉树的实现

从上面我们知道，可以用左右来区分二叉树的两个节点。

二叉树节点的声明：

1 typedef struct TreeNode *PtrNode;
2 typedef struct PtrToNode Tree;
3 
4 struct TreeNode
5 {
6     ElementType Element;
7     Tree Left;
8     Tree Right;
9 };

5.多叉树

描述：树中各节点的子节点数目不确定，且每个节点的子节点均不超过K个的有根树，称为K叉树。

多叉树的实现

父节点表示法：

在树结构中，除根节点以外的节点都是有且仅有一个父节点，按照这个思路，只需在每一个节点中储存对应的父节点的指针，就能将所有节点组织起来。

这样一来，节点的声明就可以写成这样。

1 typedef struct TreeNode_Father *PtrNode;
2 typedef struct PtrToNode Tree;
3 
4 struct TreeNode_Father
5 {
6     ElementType Element;
7     Tree FatherNode;
8 };

这样实现的多叉树，仅需常数时间O(1)即可确定任一节点的父节点，但查找子节点将不得不遍历所有节点，花费O(n)的时间。

子节点表示法：在每个节点中，储存该节点指向的所有子节点的指针。

这样，子节点的查找将能快速实现，但将所有的节点以这样的方法组织起来却并不容易，因为每个节点的子节点数目并不相同，即每个节点并不具有一般性规律，维护起来将很麻烦。

父节点+子节点表示法：如果结合父节点和子节点表示法的优势，在每个节点中同时记录其父节点和所有子节点，就可以高效地兼顾对父节点和子节点的定位。

然而，当此类树涉及到插入删除操作时，每对一个节点进行操作，就必须要对其相应的子序列进行调整，以维护和更新树的拓扑结构。而线性结构完成这些操作都需要花费大量时间。

长子兄弟法：将树的节点的特征抽象出来，我们发现，每个父节点下面都连接着若干（或0）个子节点，把左起第一个子节点记作FirstChild（长子），后面的子节点分别是上一个子节点的NextSibling（兄弟）。

具体的节点声明如下：

1 typedef struct TreeNode *PtrToNode;
2 
3 struct TreeNode
4 {
5     ElementType Element;
6     PtrToNode FirstChild;
7     PtrToNode NextSibling;
8 };

这样实现的一棵树形如下图：

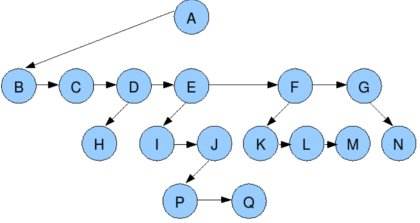
由上我们知道，树结构具有一定的线性特征。

因为同一节点的所有子节点具有线性次序，那么，将长子看作左节点，其他兄弟看作右节点，所有的多叉树都能被看作二叉树。

这种多叉树也叫有序树。

6.BinNode模板类（关于节点的功能）

 1 #define BinNodePosi(T) BinNode<T>* //节点位置
 2 #define stature(p) ((p) ? (p)->height : -1) //节点高度（与“空树高度为-1”的约定相统一）
 3 typedef enum { RB_RED, RB_BLACK} RBColor; //节点颜色
 4 
 5 template <typename T> struct BinNode { //二叉树节点模板类
 6 // 成员（为简化描述起见统一开放，读者可根据需要进一步封装）
 7    T data; //数值
 8    BinNodePosi(T) parent; BinNodePosi(T) lc; BinNodePosi(T) rc; //父节点及左、右孩子，均为指针类型
 9    int height; //高度（通用）
10    int npl; //Null Path Length（左式堆，也可直接用height代替）
11    RBColor color; //颜色（红黑树）
12 // 构造函数
13    BinNode() :
14       parent ( NULL ), lc ( NULL ), rc ( NULL ), height ( 0 ), npl ( 1 ), color ( RB_RED ) { }
15    BinNode ( T e, BinNodePosi(T) p = NULL, BinNodePosi(T) lc = NULL, BinNodePosi(T) rc = NULL,
16              int h = 0, int l = 1, RBColor c = RB_RED ) :
17       data ( e ), parent ( p ), lc ( lc ), rc ( rc ), height ( h ), npl ( l ), color ( c ) { }
18 // 操作接口
19    int size(); //统计当前节点后代总数，亦即以其为根的子树的规模
20    BinNodePosi(T) insertAsLC ( T const& ); //作为当前节点的左孩子插入新节点
21    BinNodePosi(T) insertAsRC ( T const& ); //作为当前节点的右孩子插入新节点
22    BinNodePosi(T) succ(); //取当前节点的直接后继
23    template <typename VST> void travLevel ( VST& ); //子树层次遍历
24    template <typename VST> void travPre ( VST& ); //子树先序遍历
25    template <typename VST> void travIn ( VST& ); //子树中序遍历
26    template <typename VST> void travPost ( VST& ); //子树后序遍历
27 // 比较器、判等器（各列其一，其余自行补充），重载运算符
28    bool operator< ( BinNode const& bn ) { return data < bn.data; } //小于
29    bool operator== ( BinNode const& bn ) { return data == bn.data; } //等于
30    /*DSA*/
31    /*DSA*/BinNodePosi(T) zig(); //顺时针旋转
32    /*DSA*/BinNodePosi(T) zag(); //逆时针旋转
33 };

↑代码来自《数据结构（C++语言版）》邓俊辉

在后续实现中，将频繁用到二叉树的各种功能，不妨用宏定义的方式将这些常用功能整理归纳。

 1 #define IsRoot(x) (!((x).parent))
 2 #define IsLChild(x) (!IsRoot(x)&&(&(x)==(x).parent->lc))
 3 #define IsRChild(x) (!IsRoot(x)&&(&(x)==(x).parent->rc))
 4 #define HasParent(x) (!IsRoot(x))
 5 #define HasLChild(x) ((x).lc)
 6 #define HasRChild(x) ((x).rc)
 7 #define HasChild(x) (HasLChild(x)||HasRChild(x))
 8 #define HasBothChild(x) (HasLChild(x)&&HasRChild(x))
 9 #define IsLeaf(x) (!HasChild(x))
10 #define Sibling(p) (IsLChild(*(p))?(p)->parent->rc:(p)->parent->lc)
11 #define Uncle(x) (IsChild(*((x)->parent))?(x)->parent->parent->rc:(x)->parent->parent->lc)
12 #define FromParentTo(x) (IsRoot(x)?_root:(IsChild(x)?(x).parent->lc:(x).parent->rc))

插入节点：

1 template <typename T> BinNodePosi(T) BinNode<T>::insertAsLC(T const& e)
2 {return lc=new BinNode (e,this);}//作为左子节点插入
3 
4 template <typename T> BinNodePosi(T) BinNode<T>::insertAsRC(T const& e)
5 {return rc=new BinNode (e,this);}//作为右子节点插入

7.BinTree模板（关于树的功能）

 1 #include "BinNode.h" //引入二叉树节点类
 2 template <typename T> class BinTree { //二叉树模板类
 3 protected:
 4    int _size; BinNodePosi(T) _root; //规模、根节点
 5    virtual int updateHeight ( BinNodePosi(T) x ); //更新节点x的高度
 6    void updateHeightAbove ( BinNodePosi(T) x ); //更新节点x及其祖先的高度
 7 public:
 8    BinTree() : _size ( 0 ), _root ( NULL ) { } //构造函数
 9    ~BinTree() { if ( 0 < _size ) remove ( _root ); } //析构函数
10    int size() const { return _size; } //规模
11    bool empty() const { return !_root; } //判空
12    BinNodePosi(T) root() const { return _root; } //树根
13    BinNodePosi(T) insertAsRoot ( T const& e ); //插入根节点
14    BinNodePosi(T) insertAsLC ( BinNodePosi(T) x, T const& e ); //e作为x的左孩子（原无）插入
15    BinNodePosi(T) insertAsRC ( BinNodePosi(T) x, T const& e ); //e作为x的右孩子（原无）插入
16    BinNodePosi(T) attachAsLC ( BinNodePosi(T) x, BinTree<T>* &T ); //T作为x左子树接入
17    BinNodePosi(T) attachAsRC ( BinNodePosi(T) x, BinTree<T>* &T ); //T作为x右子树接入
18    int remove ( BinNodePosi(T) x ); //删除以位置x处节点为根的子树，返回该子树原先的规模
19    BinTree<T>* secede ( BinNodePosi(T) x ); //将子树x从当前树中摘除，并将其转换为一棵独立子树
20    template <typename VST> //操作器
21    void travLevel ( VST& visit ) { if ( _root ) _root->travLevel ( visit ); } //层次遍历
22    template <typename VST> //操作器
23    void travPre ( VST& visit ) { if ( _root ) _root->travPre ( visit ); } //先序遍历
24    template <typename VST> //操作器
25    void travIn ( VST& visit ) { if ( _root ) _root->travIn ( visit ); } //中序遍历
26    template <typename VST> //操作器
27    void travPost ( VST& visit ) { if ( _root ) _root->travPost ( visit ); } //后序遍历
28    bool operator< ( BinTree<T> const& t ) //比较器（其余自行补充）
29    { return _root && t._root && lt ( _root, t._root ); }
30    bool operator== ( BinTree<T> const& t ) //判等器
31    { return _root && t._root && ( _root == t._root ); }
32    /*DSA*/
33    /*DSA*/void stretchToLPath() { stretchByZag ( _root ); } //借助zag旋转，转化为左向单链
34    /*DSA*/void stretchToRPath() { stretchByZig ( _root, _size ); } //借助zig旋转，转化为右向单链
35 }; //BinTree

高度更新：

二叉树任一节点的高度，都等于其子节点的最大高度+1

当某一节点的高度发生改变时，其所有祖先的高度都将发生改变。

那么，我们可以从当前节点（高度首先发生变化的节点）开始，沿着parent指针的方向，向上回溯，依次更新其所有祖先的高度。

1 template <typename T> int BinTree<T>::updateHeight ( BinNodePosi(T) x ) //更新节点x高度
2 { return x->height = 1 + max ( stature ( x->lc ), stature ( x->rc ) ); } //具体规则，因树而异
3 
4 template <typename T> void BinTree<T>::updateHeightAbove ( BinNodePosi(T) x ) //更新高度
5 { while ( x ) { updateHeight ( x ); x = x->parent; } } //从x出发，覆盖历代祖先。可优化

节点插入：

每次插入记得更新树的高度和全树规模

1 template <typename T> BinNodePosi(T) BinTree<T>::insertAsRoot ( T const& e )
2 { _size = 1; return _root = new BinNode<T> ( e ); } //将e当作根节点插入空的二叉树
3 
4 template <typename T> BinNodePosi(T) BinTree<T>::insertAsLC ( BinNodePosi(T) x, T const& e )
5 { _size++; x->insertAsLC ( e ); updateHeightAbove ( x ); return x->lc; } //e插入为x的左孩子
6 
7 template <typename T> BinNodePosi(T) BinTree<T>::insertAsRC ( BinNodePosi(T) x, T const& e )
8 { _size++; x->insertAsRC ( e ); updateHeightAbove ( x ); return x->rc; } //e插入为x的右孩子

子树接入：

将要接入的子树的根节点赋给某节点的子节点

 1 template <typename T> //二叉树子树接入算法：将S当作节点x的左子树接入，S本身置空
 2 BinNodePosi(T) BinTree<T>::attachAsLC ( BinNodePosi(T) x, BinTree<T>* &S ) { //x->lc == NULL
 3    if ( x->lc = S->_root ) x->lc->parent = x; //接入
 4    _size += S->_size; updateHeightAbove ( x ); //更新全树规模与x所有祖先的高度
 5    S->_root = NULL; S->_size = 0; release ( S ); S = NULL; return x; //释放原树，返回接入位置
 6 }
 7 
 8 template <typename T> //二叉树子树接入算法：将S当作节点x的右子树接入，S本身置空
 9 BinNodePosi(T) BinTree<T>::attachAsRC ( BinNodePosi(T) x, BinTree<T>* &S ) { //x->rc == NULL
10    if ( x->rc = S->_root ) x->rc->parent = x; //接入
11    _size += S->_size; updateHeightAbove ( x ); //更新全树规模与x所有祖先的高度
12    S->_root = NULL; S->_size = 0; release ( S ); S = NULL; return x; //释放原树，返回接入位置
13 }

子树删除：

 1 template <typename T> //删除二叉树中位置x处的节点及其后代，返回被删除节点的数值
 2 int BinTree<T>::remove ( BinNodePosi(T) x ) { //assert: x为二叉树中的合法位置
 3    FromParentTo ( *x ) = NULL; //切断来自父节点的指针
 4    updateHeightAbove ( x->parent ); //更新祖先高度
 5    int n = removeAt ( x ); _size -= n; return n; //删除子树x，更新规模，返回删除节点总数
 6 }
 7 template <typename T> //删除二叉树中位置x处的节点及其后代，返回被删除节点的数值
 8 static int removeAt ( BinNodePosi(T) x ) { //assert: x为二叉树中的合法位置
 9    if ( !x ) return 0; //递归基：空树
10    int n = 1 + removeAt ( x->lc ) + removeAt ( x->rc ); //递归释放左、右子树
11    release ( x->data ); release ( x ); return n; //释放被摘除节点，并返回删除节点总数
12 }

子树分离：

1 template <typename T> //二叉树子树分离算法：将子树x从当前树中摘除，将其封装为一棵独立子树返回
2 BinTree<T>* BinTree<T>::secede ( BinNodePosi(T) x ) { //assert: x为二叉树中的合法位置
3    FromParentTo ( *x ) = NULL; //切断来自父节点的指针
4    updateHeightAbove ( x->parent ); //更新原树中所有祖先的高度
5    BinTree<T>* S = new BinTree<T>; S->_root = x; x->parent = NULL; //新树以x为根
6    S->_size = x->size(); _size -= S->_size; return S; //更新规模，返回分离出来的子树
7 }

8.二叉树的遍历方法

我们根据访问根节点的次序来分类二叉树的遍历方法。

根节点（V），左子节点（L），右子节点（R）

先序遍历：V | L | R

中序遍历：L | V | R

后序遍历：L | R | V

层序遍历：从左到右按层遍历

9.先序遍历

递归版本：

由于二叉树本身的定义便带有递归的性质，所以很容易得出递归解法

1 template <typename T,typename VST>//元素类型，操作器
2 void travPre_R (BinNodePosi(T) x,VST& visit)
3 {
4     if(!x) return;
5     visit(x->data);
6     travPre_R(x->lc,visit);
7     travPre_R(x->rc,visit);
8 }

迭代版本1：

因为递归版本的时间、空间复杂度的常系数较大，所以虽然其整体复杂度只有O(n)，但实际应用时效率不高。

将递归改写为迭代可以有效将时间空间复杂度常系数缩小。

观察递归版本可知，该实现是尾递归的形式，改写成迭代很容易。

 1 template <typename T,typename VST>//元素类型，操作器
 2 void travPre_I1(BinNodePosi(T) x,VST& visit)
 3 {
 4     Stack<BinNodePosi(T)> S;//辅助栈
 5     if(x) S.push(x);//根节点入栈
 6     while(!S.empty())//栈空前一直循环
 7     {
 8         x=S.pop();
 9         visit(x->data);
10         if(HasRChild(*x))//入栈顺序是先右后左
11             S.push(x->rc);
12         if(HasLChild(*x))
13             S.push(x->lc);//出栈顺序是先左后右
14     }
15 }

迭代版本2：

版本1并不适用于尾递归以外的场景，当我们试图将这种思路推广到中序遍历和后序遍历时将遇到困难。

另一个思路是，观察二叉树的遍历顺序，可以得知，遍历开始时，总是从根节点出发，访问左子节点，然后访问左子节点的左子节点... ...直到遇到一个节点没有左子节点时，将这个节点记作v，访问v的右子节点，然后向上回溯，访问v的父节点的右子节点（即v的兄弟节点），然后从v的兄弟节点出发，重复“访问左子节点，向上回溯”的过程... ...

简而言之，从当前节点开始，沿左分支不断深入，直到没有左节点的分支，从该节点开始自下而上访问其右子树。访问右子树的方式与上面相同。

代码实现：

 1 //从当前节点出发，沿左分支不断深入，直至没有左分支的节点；沿途节点遇到后立即访问
 2 template <typename T, typename VST> //元素类型、操作器
 3 static void visitAlongLeftBranch ( BinNodePosi(T) x, VST& visit, Stack<BinNodePosi(T)>& S ) {
 4    while ( x ) {
 5       visit ( x->data ); //访问当前节点
 6       S.push ( x->rc ); //右孩子入栈暂存（可优化：通过判断，避免空的右孩子入栈）
 7       x = x->lc;  //沿左分支深入一层
 8    }
 9 }
10 
11 template <typename T, typename VST> //元素类型、操作器
12 void travPre_I2 ( BinNodePosi(T) x, VST& visit ) { //二叉树先序遍历算法（迭代版#2）
13    Stack<BinNodePosi(T)> S; //辅助栈
14    while ( true ) {
15       visitAlongLeftBranch ( x, visit, S ); //从当前节点出发，逐批访问
16       if ( S.empty() ) break; //直到栈空
17       x = S.pop(); //弹出下一批的起点
18    }
19 }

后序遍历可以直接沿用迭代版本2的思路。

10.中序遍历

递归版本：

和前序遍历一样，递归版本可以很简洁地实现

1 template <typename T,typename VST>//元素类型，操作器
2 void travIn_R (BinNodePosi(T) x,VST& visit)
3 {
4     if(!x) return;
5     travIn_R(x->lc,visit);
6     visit(x->data);
7     travIn_R(x->rc,visit);
8 }

不同的是，中序遍历并不是尾递归，不能将其直接改写为迭代版本。

迭代版本1：

中序遍历从根节点开始，首先访问的却不是根节点，而是整棵树最左边的叶节点。控制权由根节点开始，依次向下交给左子节点，直到某节点没有左子节点，访问该节点，然后访问其右子树（如果有的话），然后向上回溯到该节点的父节点，访问其右子树... ...

概括起来就是，中序遍历可以沿其左通路，以沿途节点为界，将整个中序遍历的过程划分为d+1段。

每一段的过程是，访问左通路上的某节点，再遍历其对应的右子树。一段完成以后，转到左通路上的上一个节点，重复该过程。

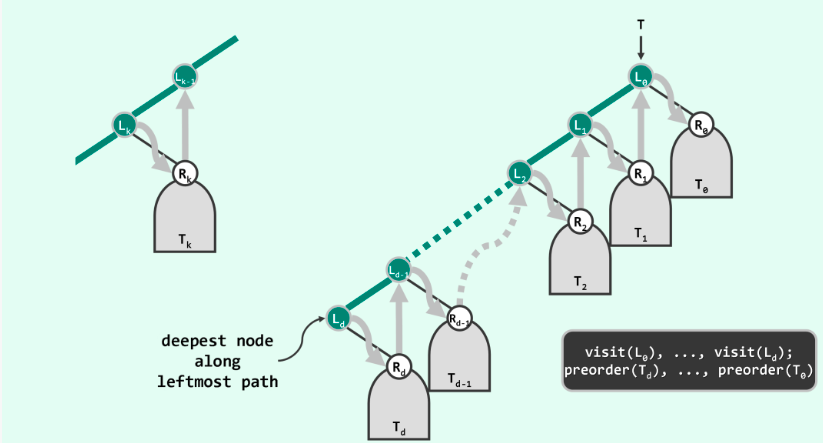
↑中序遍历过程的分解

具体代码实现为：

 1 template <typename T> //从当前节点出发，沿左分支不断深入，直至没有左分支的节点
 2 static void goAlongLeftBranch ( BinNodePosi(T) x, Stack<BinNodePosi(T)>& S ) {
 3    while ( x ) { S.push ( x ); x = x->lc; } //当前节点入栈后随即向左侧分支深入，迭代直到无左孩子
 4 }
 5 
 6 template <typename T, typename VST> //元素类型、操作器
 7 void travIn_I1 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#1）
 8    Stack<BinNodePosi(T)> S; //辅助栈
 9    while ( true ) {
10       goAlongLeftBranch ( x, S ); //从当前节点出发，逐批入栈
11       if ( S.empty() ) break; //直至所有节点处理完毕
12       x = S.pop(); visit ( x->data ); //弹出栈顶节点并访问之
13       x = x->rc; //转向右子树
14    }
15 }

首先调用函数goAlongLeftBranch，沿左通路向下，到达最左侧的叶节点，利用辅助栈记录沿途的节点，用后进先出的性质实现实际的访问顺序。

直接后继：中序遍历的大致思路还是将树这样一种非线性结构转化为线性结构，使其遍历按照线性的顺序，而一旦树具有了线性的顺序，和向量链表等一样，二叉树的节点一样具有其前驱和后继，而确定二叉树节点的直接后继，将在后续算法中起到重要的作用。

代码实现如下：

 1 template <typename T> BinNodePosi(T) BinNode<T>::succ() { //定位节点v的直接后继
 2    BinNodePosi(T) s = this; //记录后继的临时变量
 3    if ( rc ) { //若有右孩子，则直接后继必在右子树中，具体地就是
 4       s = rc; //右子树中
 5       while ( HasLChild ( *s ) ) s = s->lc; //最靠左（最小）的节点
 6    } else { //否则，直接后继应是“将当前节点包含于其左子树中的最低祖先”，具体地就是
 7       while ( IsRChild ( *s ) ) s = s->parent; //逆向地沿右向分支，不断朝左上方移动
 8       s = s->parent; //最后再朝右上方移动一步，即抵达直接后继（如果存在）
 9    }
10    return s;
11 }

迭代版本2：对迭代版本1进行改写简化

 1 template <typename T, typename VST> //元素类型、操作器
 2 void travIn_I2 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#2）
 3    Stack<BinNodePosi(T)> S; //辅助栈
 4    while ( true )
 5       if ( x ) {
 6          S.push ( x ); //根节点进栈
 7          x = x->lc; //深入遍历左子树
 8       } else if ( !S.empty() ) {
 9          x = S.pop(); //尚未访问的最低祖先节点退栈
10          visit ( x->data ); //访问该祖先节点
11          x = x->rc; //遍历祖先的右子树
12       } else
13          break; //遍历完成
14 }

迭代版本3：

以上两个版本都需要用到辅助栈，而在最坏情况下，辅助栈所占用的空间规模将和二叉树的规模相当，为此，借助parent指针和succ（直接后继定位函数），可以有效节约空间开销。

时间复杂度有所牺牲。

 1 template <typename T, typename VST> //元素类型、操作器
 2 void travIn_I3 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#3，无需辅助栈）
 3    bool backtrack = false; //前一步是否刚从右子树回溯——省去栈，仅O(1)辅助空间
 4    while ( true )
 5       if ( !backtrack && HasLChild ( *x ) ) //若有左子树且不是刚刚回溯，则
 6          x = x->lc; //深入遍历左子树
 7       else { //否则——无左子树或刚刚回溯（相当于无左子树）
 8          visit ( x->data ); //访问该节点
 9          if ( HasRChild ( *x ) ) { //若其右子树非空，则
10             x = x->rc; //深入右子树继续遍历
11             backtrack = false; //并关闭回溯标志
12          } else { //若右子树空，则
13             if ( ! ( x = x->succ() ) ) break; //回溯（含抵达末节点时的退出返回）
14             backtrack = true; //并设置回溯标志
15          }
16       }
17 }

用一个布尔类型的变量backtrack指示此前是否已经做过一次自下而上的回溯，节省栈的空间开销。

但也因此无法直接获得回溯时的访问节点的顺序（不能借助栈后进先出的性质），需要反复调用succ接口，不断确定当前节点的直接后继，以确定访问顺序。

当succ返回的直接后继为NULL时，也就意味着遍历完成了。

11.层次遍历

层次遍历非常好理解，从左往右逐层向下访问节点即可。

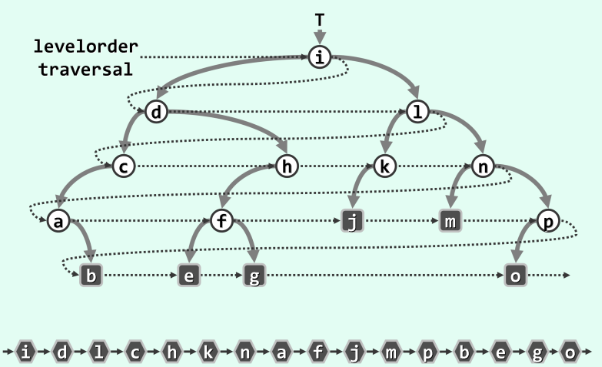
上面的先序遍历中序遍历采用了辅助栈，而层次遍历则采用队列结构。

 1 /*DSA*/#include "../queue/queue.h" //引入队列
 2 template <typename T> template <typename VST> //元素类型、操作器
 3 void BinNode<T>::travLevel ( VST& visit ) { //二叉树层次遍历算法
 4    Queue<BinNodePosi(T)> Q; //辅助队列
 5    Q.enqueue ( this ); //根节点入队
 6    while ( !Q.empty() ) { //在队列再次变空之前，反复迭代
 7       BinNodePosi(T) x = Q.dequeue(); visit ( x->data ); //取出队首节点并访问之
 8       if ( HasLChild ( *x ) ) Q.enqueue ( x->lc ); //左孩子入队
 9       if ( HasRChild ( *x ) ) Q.enqueue ( x->rc ); //右孩子入队
10    }
11 }

12.二叉树的应用

表达式树，PFC编码树，Huffman编码树

挖坑待填。

填坑，数据结构应用 - 二叉树

参考资料【1】《数据结构（C++语言版）》邓俊辉

　　　　【2】《数据结构与算法分析——C语言描述》 Mark Allen Weiss