邻项交换排序
通过找到 决定 相邻两个单位位置 的策略 以推广到整个队伍,是一种通过贪心解决问题的方法。
题目大意
有n个大臣,第i位大臣左手的数为ai,右手的数为bi,且ai和bi均为正整数。他能获得的数ci由以下关系给出:
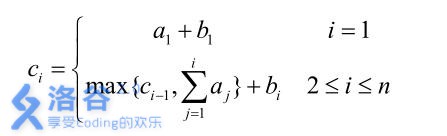
求ci最大的大臣的ci最小为多少。
分析
Part 1
我们要找大臣的顺序,且排列顺序没有后效性,我们不妨拎出相邻的大臣i与大臣j。
设这两位大臣之前的大臣获得的奖金为y,之前的所有大臣左手上的数之和为x。
①当大臣1排在大臣2之前时:
大臣i的奖金:max( y,x+ai )+bi
大臣j的奖金:max( ci,x+ai+aj )+bj
②当大臣1排在大臣2之前时:
大臣j的奖金:max( y,x+aj )+bj
大臣i的奖金:max( cj,x+ai+aj )+bi
我们比较两种情况,分析满足何种条件时我们才能把大臣i放在前面。
显然,当一个大臣被放在后面时,一定比他放在前面时得到的奖金多(证明略)
为了比较奖金最多大臣的奖金多少,我们进而比较被放在后面时两个大臣的奖金数。
为使情况最优,max( ci,x+ai+aj )+bj < max( cj,x+ai+aj )+bi
=> max( max( y,x+ai )+bi,x+ai+aj )+bj < max( max( y,x+aj )+bj,x+ai+aj )+bi
=> max( y+bi,x+ai+bi,x+ai+aj )+bj < max( y+bj,x+aj+bj,x+ai+aj )+bi
=> max( y+bi+bj,x+ai+bi+bj,x+ai+aj +bj) < max( y+bj+bi,x+aj+bj+bi,x+ai+aj+bi )
由于两式中都有 y+bi+bj,我们忽略不计算。
=> max( x+ai+bi+bj,x+ai+aj +bj) < max( x+aj+bj+bi,x+ai+aj+bi )
为化简式子,我们同时减去 x+ai+aj+bi+bj
=> max( -aj,-bi) < max( -ai,-bj )
=> min( aj,bi ) < min( ai,bj )
Part 2
于是如果您的sort的cmp函数写成:
bool operator <(node a) const { return min(x,a.y)<min(y,a.x); }
或许能水过洛谷的数据,但是是错解。
这里从Luogu题解中找到了一组hack数据:
2
7
6 3
1 1
7 3
1 1
1 6
1 1
6 10
7
6 10
1 1
6 3
1 1
7 3
1 1
1 6
上面两组数据只是顺序不一样,结果应该是一样的,但用上面的程序跑出来的结果却是不一样的。
再具体地分析一下。假设有三位大臣,他们的a[i]和b[i]分别是:
7 3
1 1
1 6
显然,这样可以是排完序后的结果,因为两两之间用条件判断都是等于。这样算出来答案是17。而如果这样排:
1 1
1 6
7 3
答案是12,显然这样更优,但程序却有可能排成17的那种情况。
为什么错了呢?简单来说,就是此时的判断条件不满足传递性。引用一个名词——严格弱序。sort的判断函数必须满足严格弱序。
严格弱序是什么?
拿内置类型来说,C++都定义了 “<”操作符,这就是一个严格弱序,而“<=”就不是一个严格弱序
对于内置类型我们自然可以有<、>、=来判断两个值的大小关系,而对于自定义的类型,只用一个严格弱序(这里就用<为例)就可以表示两个元素三种大小关系
a小于b
a < b
b小于a
b < a
a等于b
!(a < b) && !( b < a )
严格弱序的三点要求:
1.两个关键字不能同时“严格弱序”于对方
2.如果a“严格弱序”于b,且b“严格弱序”于c,则a必须“严格弱序”于c(传递性)
3.如果存在两个关键字,任何一个都不“严格弱序”于另一个,则这两个关键字是相等的。
摘自WikiPedia的定义:
A strict weak ordering is a binary relation < on a set S that is a strict partial order (a transitive relation that is irreflexive, or equivalently,[5] that is asymmetric) in which the relation "neither a < b nor b < a" is transitive.[1] Therefore, a strict weak ordering has the following properties:
- For all x in S, it is not the case that x < x (irreflexivity).
- For all x, y in S, if x < y then it is not the case that y < x (asymmetry).
- For all x, y, z in S, if x < y and y < z then x < z (transitivity).
- For all x, y, z in S, if x is incomparable with y (neither x < y nor y < x hold), and y is incomparable with z, then x is incomparable with z (transitivity of incomparability).
This list of properties is somewhat redundant, as asymmetry follows readily from irreflexivity and transitivity.
非严格弱序带来的问题:
有序关联容器不允许存在相同的关键字,在判断时,会认为相同的关键字是不相等的,因此会将两个相同的关键字插入容器中,这个行为是未定义的。

注:以上部分严格弱序的叙述摘自 C++ 严格弱序 River_Lethe
Part 3
那么,如果必须使用严格弱序,应该如何判断 min( aj,bi ) < min( ai,bj ) 呢?
我们分情况讨论:
1.当ai < bi,aj < bj时,ai ≤ aj,应该按a升序排序(ai和aj相等时无所谓)。
2.当ai = bi,aj = bj时,爱怎么排怎么排。
3.当ai > bi,aj > bj时,bi ≥ bj,应该按b降序排序。
//判断a[i].x 与 b[i].x 的大小关系 if (a[i].x>a[i].y) a[i].d=1; else if (a[i].x<a[i].y) a[i].d=-1; else a[i].d=0;
于是cmp将是这样的:
bool operator <(node a) const { if (d!=a.d) return d<a.d; if (d<=0) return x<a.x; return y>a.y; }