$EL Gamal$ 密码方案的椭圆曲线形式

(EL Gamal) 密码方案的椭圆曲线形式

(1.) 问题背景

公私钥生成 令 (E) 为 (F_{q}) 上的椭圆曲线，一般记为 (E(F_{q}))，设 (P = (x_{p}, y_{p})in E(F_{q}))，且 (P) 的阶数为大素数，取 (sin F_{q})，满足 (1 < s < ord(P))，令 (Q = (x_{q}, y_{q}) = sP)，则 ((E(F_{q}), P, Q)) 为公钥，(s) 为私钥

加密过程 将消息 (m) 映射到 (F_{q}^{*})，任取 (1 < r < ord(P))，计算 ((x_{1}, y_{1}) = rP, (x_{2}, y_{2}) = rQ, c = mcdot x_{2})，则密文为 ((x_{1}, y_{1}, c))

解密过程 计算 ((x', y') = scdot (x_{1}, y_{1}) = scdot rP)，再计算 (m' = ccdot x'^{-1})，解得明文，这是因为 (c = mcdot scdot rcdot x_{p}, x' = scdot rcdot x_{p})，所以 (m' = (mcdot scdot rcdot x_{p})cdot (scdot rcdot x_{p})^{-1} = m)

(2.) 问题描述

问题描述如下

  • 令 (E: y^2 = x^3 + x + 6) 为 (F_{11}) 上的一条椭圆曲线，求 (E) 上所有点
  • 令 (P = (2, 7))，取 (s = 5)，求公钥
  • 设消息 (m = 3)，取 (r = 7)，计算 (m) 的密文 ((x_{1}, y_{1}, c))
  • 对 ((x_{1}, y_{1}, c)) 做解密运算，求 ((x', y'))，并进一步求其明文 (m')

(3.) 问题分析与解

(3.1) 求 (E(F_{11})) 上所有点

令 (x_{i}, y_{j}) 遍历 (F_{11}) 上所有元素，验证是否满足 (y_{j}^2equiv x_{i}^3 + x_{i} + 6 (mod 11))

或者，令 (x_{i}) 遍历 (F_{11}) 上所有元素，计算二次剩余 (y^2equiv x_{i}^3 + x_{i} + 6 (mod 11))

我们选择第一个方法进行计算，将满足题意的点加入集合 (ans)，时间复杂度为 (O(q^2))，(q) 为域 (F_{q}) 的大小

相关代码如下

/* 得到 E(F11) 上所有点 */
void getAllPoints()
{
    for(int x = 0; x < MOD; ++x) {
        for(int y = 0; y < MOD; ++y) {
            if(qpow(y, 2) == addMOD(qpow(x, 3), addMOD(mulMOD(A, x), B))) {
                ans.pb({x, y});
            }
        }
    }
    ans.pb(O);
}

/* 输出点坐标 */
void out(pii P) {printf("(%d, %d)
", P.fi, P.se);}

/* 展示 E(F11) 上所有点 */
void showAllPoints()
{
    printf("一共有 %d 个点
", ans.size());
    for(auto i: ans) out(i);
    puts("");
}

(3.2) 令 (P = (2, 7))，取 (s = 5)，求公钥

公钥 ((E(F_{11}), P)) 已知，最后一个公钥参数即为椭圆曲线上点 (Q)，满足 (Q = sP = 5(2, 7))

为了计算 (Q = sP)，我们需要先讨论椭圆曲线上的 (1) 次加法，再椭圆曲线上的 (n) 次加法

(3.2.1) 计算 (P_{1} + P_{2} = R)

考虑椭圆曲线 (E(F_{11})) 上的加法，设 (P_{1} + P_{2} = R)，其中 (P_{1} = (x_{1}, y_{1}), P_{2} = (x_{2}, y_{2}))，则 (R = (x_{3}, y_{3})) 为直线 (P_{1}P_{2}) 与 (E(F_{11})) 的第三个交点 (R') 关于 (X) 轴的对称点

设无穷远点为 (O)，下面讨论 (P_{1}) 与 (P_{2}) 的关系，以及对应的 (R = P_{1} + P_{2}) 的求解，并给出 (R) 的显式解

易知，这样的计算时间复杂度是 (O(1))

(3.2.1.1 P_{1} = O) 或者 (P_{2} = O)

分两种情况

  • 若 (P_{1} = O)，则 (R = P_{1} + P_{2} = P_{2})
  • 若 (P_{2} = O)，则 (R = P_{1} + P_{2} = P_{1})
(3.2.1.2 P_{1} = P_{2})

当 (y_{1} = 0) 时，(k_{1} = infty)，则 (R = P_{1} + P_{2} = O)

示例图如下

1

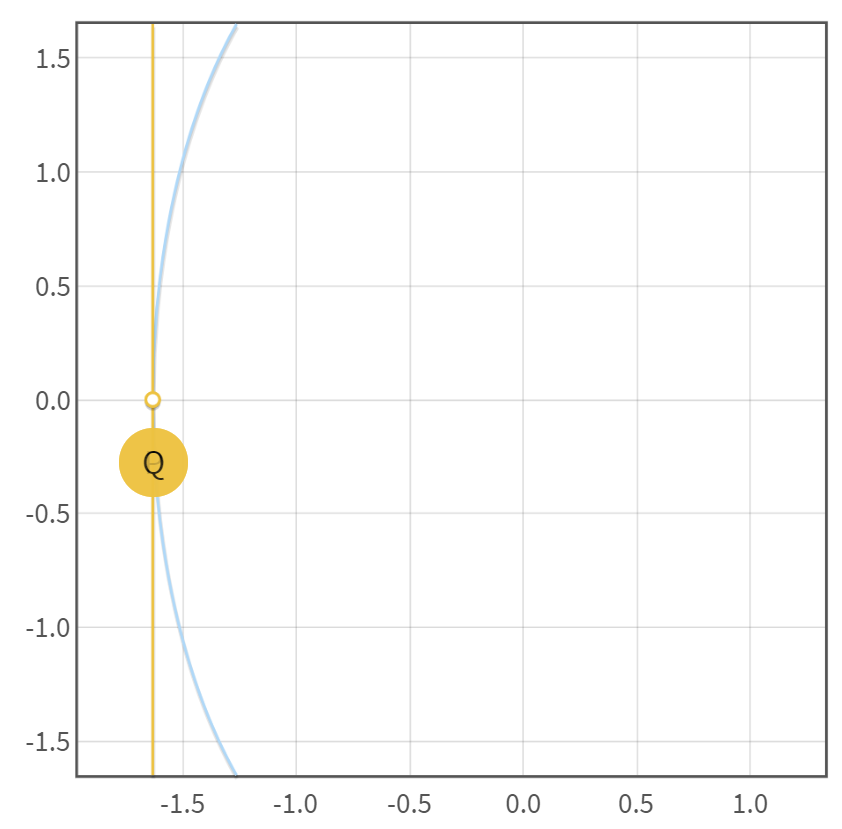
当 (y_{1} eq 0) 时，计算 (E(F_{11})) 在 (P_{1} = P_{2} = (x_{1}, y_{1})) 处的切线，设斜率为 (k_{1})

对于方程 (y^2 = x^3 + x + 6)，两边同时对 (x) 求导，得到

[2yfrac{dy}{dx} = 3x^2 + 1, frac{dy}{dx} = (3x^2 + 1)cdot (2y)^{-1} ]

所以

[k_{1} = frac{dy}{dx}mid_{x = x_{1}, y = y_{1}} = (3x_{1}^2 + 1)cdot (2y_{1})^{-1} ]

对应的切线方程为

[y = k_{1}cdot (x - x_{1}) + y_{1} ]

即

[y = (3x_{1}^2 + 1)cdot (2y_{1})^{-1}cdot (x - x_{1}) + y_{1} ]

代入椭圆方程解得

[egin{aligned} x_{R} & = k^2 - 2cdot x_{1}\ y_{R} & = MOD - [y_{1} + kcdot (x_{R} - x_{1})] end{aligned} ]

示例图如下

2

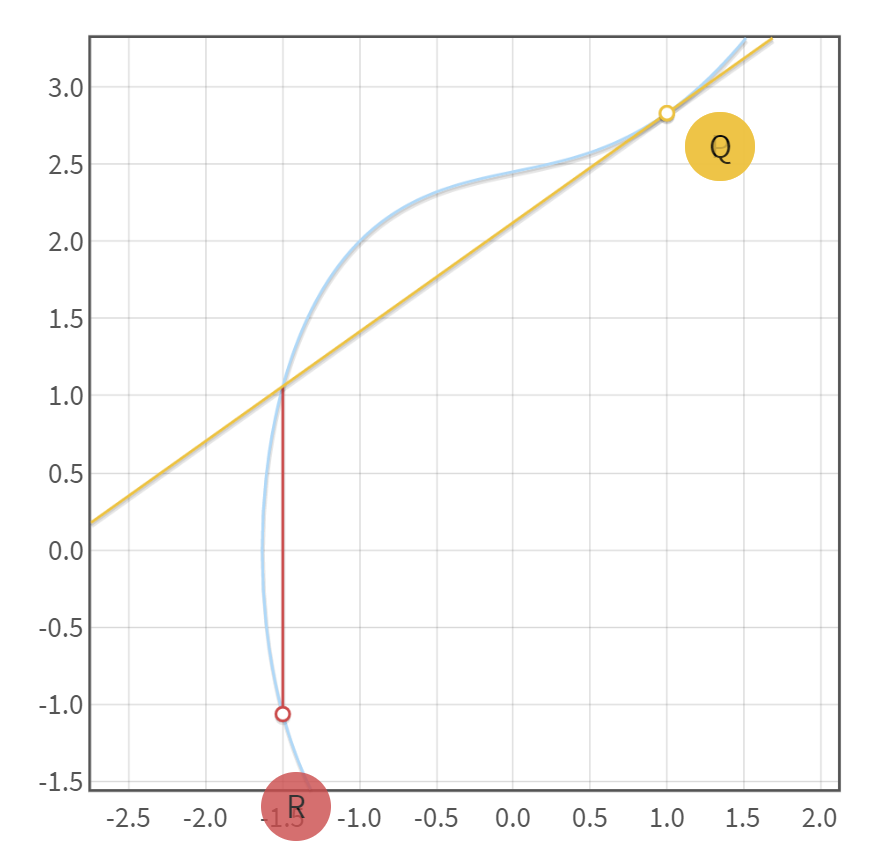
(3.2.1.3 P_{1} eq P_{2})

当 (x_{2} = x_{1}) 时，对应的第三个交点 (R) 为无穷远点 (O)

示例图如下

3

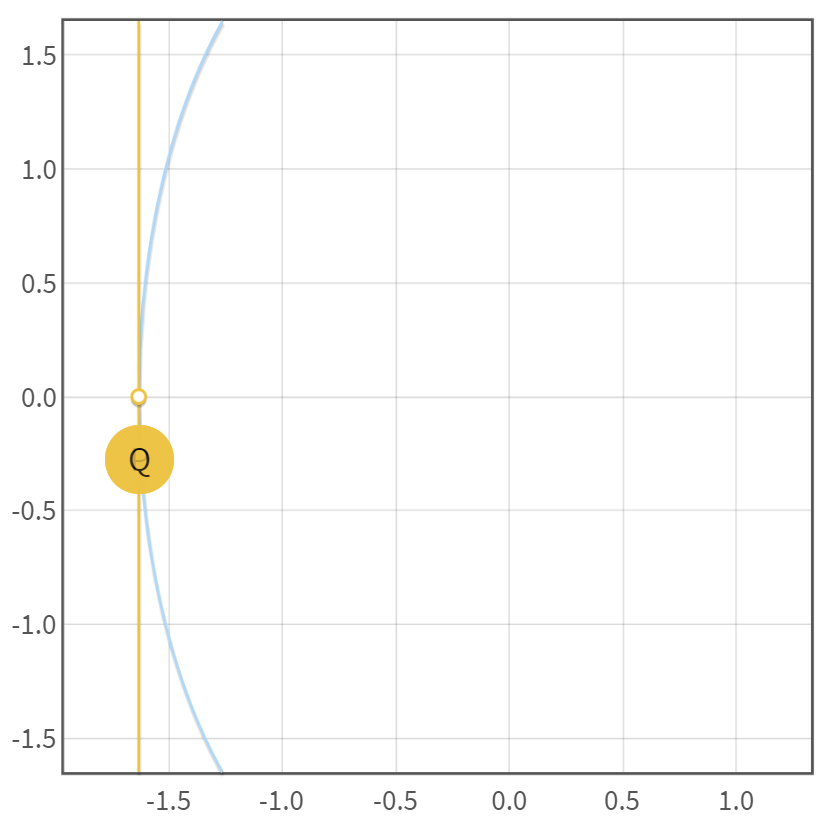
当 (x_{2} eq x_{1}) 时，直线方程 (P_{1}P_{2}) 为

[y - y_{2} = kcdot (x - x_{2}) ]

其中

[k = (y_{2} - y_{1})(x_{2} - x_{1})^{-1} ]

即

[y = (y_{2} - y_{1})cdot(x_{2} - x_{1})^{-1} cdot (x - x_{2}) + y_{2} ]

代入椭圆方程解得

[egin{aligned} x_{R} & = k^2 - x_{1} - x_{2}\ y_{R} & = MOD - [y_{1} + kcdot (x_{R} - x_{1})] end{aligned} ]

示例图如下

4

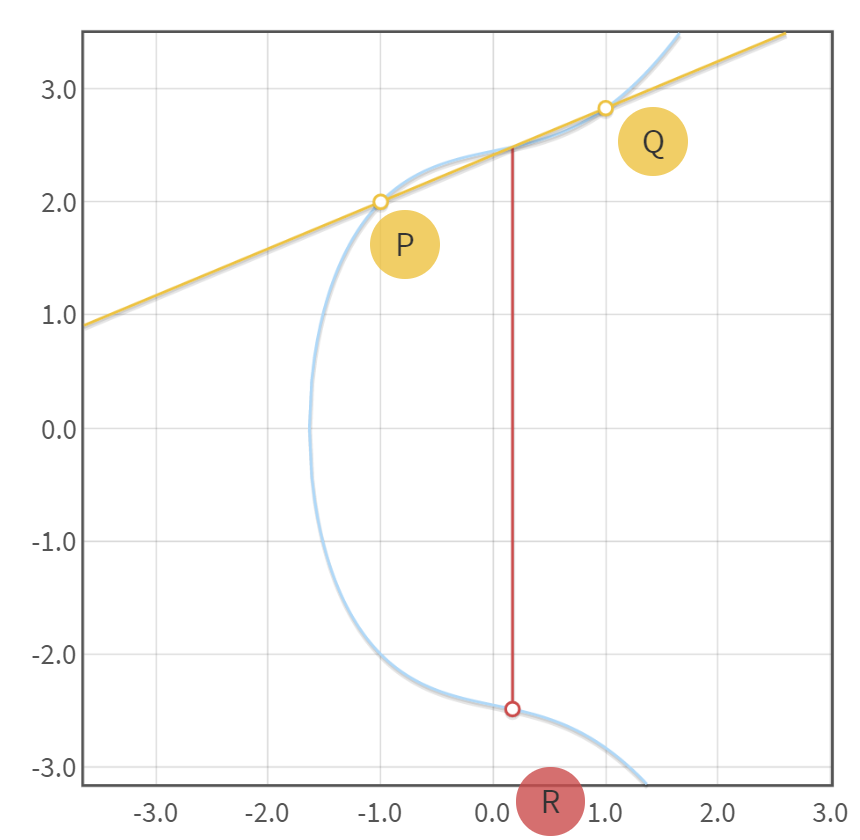
(3.2.2) 计算 (nP)

为了计算 (nP)，最简单的想法是进行 (n - 1) 次递推，算法的复杂度为 (O(n))

进一步的，我们可以利用快速幂算法将时间复杂度优化到 (O(logn))

相关代码如下

/* 计算点 P 处切线斜率 */
int getTangentAtPoint(pii P)
{
    return mulMOD(addMOD(mulMOD(3, qpow(P.fi, 2)), A), getInv(mulMOD(2, P.se)));
}

/* 计算直线 P1P2 斜率 */
int getTangentOfP1P2(pii P1, pii P2)
{
    return mulMOD(subMOD(P2.se, P1.se), getInv(subMOD(P2.fi, P1.fi)));
}

/* 处理切线 */
pii handleTangent(pii P)
{
    if(P.se == 0) return O;
    int tangentAtP = getTangentAtPoint(P);
    int xr = subMOD(qpow(tangentAtP, 2), mulMOD(P.fi, 2));
    int yr = addMOD(P.se, mulMOD(tangentAtP, subMOD(xr, P.fi)));
    return {xr, MOD - yr};
}

/* 处理割线 */
pii handleSecant(pii P1, pii P2)
{
    if(P1.fi == P2.fi) return O;
    int tangentOfP1P2 = getTangentOfP1P2(P1, P2);
    int xr = subMOD(qpow(tangentOfP1P2, 2), addMOD(P1.fi, P2.fi));
    int yr = addMOD(P1.se, mulMOD(tangentOfP1P2, subMOD(xr, P1.fi)));
    return {xr, MOD - yr};
}

/* 计算 P1P2 与 E(F11) 的第三个交点 */
pii addP1P2(pii P1, pii P2)
{
    if(P1 == O || P2 == O) return P1 == O ? P2 : P1;
    else if(P1 == P2) return handleTangent(P1);
    else if(P1 != P2) return handleSecant(P1, P2);
}

/* 点幂普通算法 */
pii getNP(pii P, int n)
{
    pii nP = O;
    for(int i = 0; i < n; ++i) {
        nP = addP1P2(nP, P);
        //cout << nP.fi << ' ' << nP.se << endl;
    }
    return nP;
}

/* 点幂快速幂算法 */
pii qGetNP(pii P, int n)
{
    if(P == O) return O;
    pii ans = O;
    while(n) {
        if(n & 1) ans = addP1P2(ans, P);
        P = addP1P2(P, P), n >>= 1;
    }
    return ans;
}

/* EL'Gamal 方案生成公钥 */
publicKey getPublicKey(pii P, int s)
{
    pii Q = qGetNP(P, s);
    publicKey pk = publicKey(P, Q);
    return pk;
}

(3.3) 设消息 (m = 3)，取 (r = 7)，计算 (m) 的密文 ((x_{1}, y_{1}, c))

考虑加密过程

消息 (m) 满足 (min F_{q}^{*})，任取 (1 < r < ord(P))，计算 ((x_{1}, y_{1}) = rP, (x_{2}, y_{2}) = rQ, c = mcdot x_{2})，则密文为 ((x_{1}, y_{1}, c))

只需要按照公式分别计算出 (rP, rQ, c) 即可

相关代码如下

/* EL'Gamal 方案加密过程 */
cipherText encryption(pii P, pii Q, int r, int m)
{
    pii rP = qGetNP(P, r); // rP = (7, 9)
    pii rQ = qGetNP(Q, r);
    int c = mulMOD(m, rQ.fi);
    cipherText ciphertext = cipherText(rP.fi, rP.se, c);
    return ciphertext;
}

(3.4) 对 ((x_{1}, y_{1}, c)) 做解密运算，求 ((x', y'))，并进一步求其明文 (m')

考虑解密过程

计算 ((x', y') = scdot (x_{1}, y_{1}) = scdot rP)，再计算 (m' = ccdot x'^{-1})，解得明文，这是因为 (c = mcdot scdot rcdot x_{p}, x' = scdot rcdot x_{p})，所以 (m' = (mcdot scdot rcdot x_{p})cdot (scdot rcdot x_{p})^{-1} = m)

只需要利用密文 (x_{1}, y_{1})，公钥 (s)，计算出 (scdot (x_{1}, y_{1}))，再根据密文 (c)，便可以计算出明文 (m = m' = ccdot x'^{-1})

相关代码如下

/* EL'Gamal 方案解密过程 */
int decryption(int x, int y, int c, int s)
{
    pii rP = {x, y};
    pii srP = qGetNP(rP, s);
    int plaintext = mulMOD(c, getInv(srP.fi));
    return plaintext;
}

(4.) 完整代码

用 (CPP) 编写，注释写在代码中

#include <iostream>
#include <vector>
#include <set>
#define pii pair<int, int>
#define fi first
#define se second
#define pb push_back
#define inf 0x3f3f3f3f
using namespace std;

const int MOD = 11;
const int A = 1;
const int B = 6;
pii O = {inf, inf};
vector<pii> ans; // 用来存储 E(F11) 上所有点

struct publicKey
{
    char* EF11 = "y^2 = x^3 + x + 6";
    pii P, Q;
    publicKey(pii _P, pii _Q): P(_P), Q(_Q) {}
};

struct cipherText
{
    int x, y, c;
    cipherText(int _x, int _y, int _c): x(_x), y(_y), c(_c) {}
};

/* 整数快速幂算法 */
int qpow(int a, int b)
{
    if(!a) return 0;
    int ans = 1;
    while(b) {
        if(b & 1) ans *= a, ans %= MOD;
        a *= a, a %= MOD, b >>= 1;
    }
    return ans;
}

/* 模运算与求逆元 */
int addMOD(int a, int b) {return (a + b) % MOD;}
int subMOD(int a, int b) {return (a % MOD - b % MOD + MOD) % MOD;}
int mulMOD(int a, int b) {return a * b % MOD;}
int getInv(int x) {return qpow(x, MOD - 2);}

/* 得到 E(F11) 上所有点 */
void getAllPoints()
{
    for(int x = 0; x < MOD; ++x) {
        for(int y = 0; y < MOD; ++y) {
            if(qpow(y, 2) == addMOD(qpow(x, 3), addMOD(mulMOD(A, x), B))) {
                ans.pb({x, y});
            }
        }
    }
    ans.pb(O);
}

/* 输出点坐标 */
void out(pii P) {printf("(%d, %d)
", P.fi, P.se);}

/* 展示 E(F11) 上所有点 */
void showAllPoints()
{
    printf("一共有 %d 个点
", ans.size());
    for(auto i: ans) out(i);
    puts("");
}

/* 计算点 P 处切线斜率 */
int getTangentAtPoint(pii P)
{
    return mulMOD(addMOD(mulMOD(3, qpow(P.fi, 2)), A), getInv(mulMOD(2, P.se)));
}

/* 计算直线 P1P2 斜率 */
int getTangentOfP1P2(pii P1, pii P2)
{
    return mulMOD(subMOD(P2.se, P1.se), getInv(subMOD(P2.fi, P1.fi)));
}

/* 处理切线 */
pii handleTangent(pii P)
{
    if(P.se == 0) return O;
    int tangentAtP = getTangentAtPoint(P);
    int xr = subMOD(qpow(tangentAtP, 2), mulMOD(P.fi, 2));
    int yr = addMOD(P.se, mulMOD(tangentAtP, subMOD(xr, P.fi)));
    return {xr, MOD - yr};
}

/* 处理割线 */
pii handleSecant(pii P1, pii P2)
{
    if(P1.fi == P2.fi) return O;
    int tangentOfP1P2 = getTangentOfP1P2(P1, P2);
    int xr = subMOD(qpow(tangentOfP1P2, 2), addMOD(P1.fi, P2.fi));
    int yr = addMOD(P1.se, mulMOD(tangentOfP1P2, subMOD(xr, P1.fi)));
    return {xr, MOD - yr};
}

/* 计算 P1P2 与 E(F11) 的第三个交点 */
pii addP1P2(pii P1, pii P2)
{
    if(P1 == O || P2 == O) return P1 == O ? P2 : P1;
    else if(P1 == P2) return handleTangent(P1);
    else if(P1 != P2) return handleSecant(P1, P2);
}

/* 点幂普通算法 */
pii getNP(pii P, int n)
{
    pii nP = O;
    for(int i = 0; i < n; ++i) {
        nP = addP1P2(nP, P);
        //cout << nP.fi << ' ' << nP.se << endl;
    }
    return nP;
}

/* 点幂快速幂算法 */
pii qGetNP(pii P, int n)
{
    if(P == O) return O;
    pii ans = O;
    while(n) {
        if(n & 1) ans = addP1P2(ans, P);
        P = addP1P2(P, P), n >>= 1;
    }
    return ans;
}

/* EL'Gamal 方案生成公钥 */
publicKey getPublicKey(pii P, int s)
{
    pii Q = qGetNP(P, s);
    publicKey pk = publicKey(P, Q);
    return pk;
}

/* EL'Gamal 方案加密过程 */
cipherText encryption(pii P, pii Q, int r, int m)
{
    pii rP = qGetNP(P, r); // rP = (7, 9)
    pii rQ = qGetNP(Q, r);
    int c = mulMOD(m, rQ.fi);
    cipherText ciphertext = cipherText(rP.fi, rP.se, c);
    return ciphertext;
}

/* EL'Gamal 方案解密过程 */
int decryption(int x, int y, int c, int s)
{
    pii rP = {x, y};
    pii srP = qGetNP(rP, s);
    int plaintext = mulMOD(c, getInv(srP.fi));
    return plaintext;
}


int main()
{
    getAllPoints();
    showAllPoints();
    pii P = {2, 7};
    int sk = 5;
    publicKey pk = getPublicKey(P, sk);
    printf("公钥为 [%s, (%d, %d), (%d, %d)]

", pk.EF11, pk.P.fi, pk.P.se, pk.Q.fi, pk.Q.se);

    int r = 7, m = 3;
    cipherText ciphertext = encryption(pk.P, pk.Q, r, m);
    printf("密文为 (%d, %d, %d)

", ciphertext.x, ciphertext.y, ciphertext.c);

    int plaintext = decryption(ciphertext.x, ciphertext.y, ciphertext.c, sk);
    printf("明文为 %d

", plaintext);
    return 0;
}
【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/ChenyangXu/p/14180803.html