赛道修建 题解

题目描述

C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建 (m) 条赛道。

C 城一共有 (n) 个路口，这些路口编号为 (1,2,…,n)，有 (n-1) 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第 (i) 条道路连接的两个路口编号为 (a_i) 和 (b_i)，该道路的长度为 (l_i)。借助这 (n-1) 条道路，从任何一个路口出发都能到达其他所有的路口。

一条赛道是一组互不相同的道路 (e_1,e_2,…,e_k)，满足可以从某个路口出发，依次经过 道路 (e_1,e_2,…,e_k)（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。

目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的 (m) 条赛道中长度最小的赛道长度最大（即 (m) 条赛道中最短赛道的长度尽可能大）

输入格式

输入文件第一行包含两个由空格分隔的正整数 (n,m)，分别表示路口数及需要修建的 赛道数。

接下来 (n-1) 行，第 (i) 行包含三个正整数 (a_i,b_i,l_i)，表示第 (i) 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 (n-1) 条道路相互到达。每行中相邻两数之间均由一个空格分隔。

输出格式

输出共一行，包含一个整数，表示长度最小的赛道长度的最大值

样例输入 #1

7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7

样例输出 #1

31

【输入输出样例 #1 说明】

所有路口及适合于修建赛道的道路如下图所示：

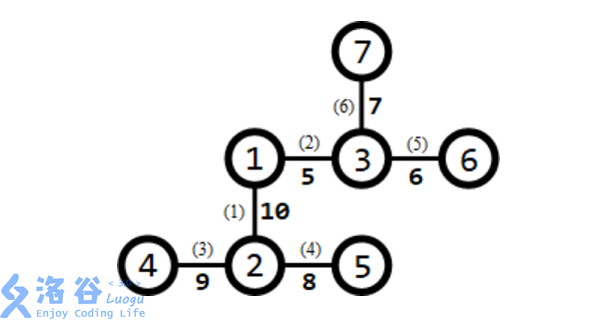
道路旁括号内的数字表示道路的编号，非括号内的数字表示道路长度。 需要修建 (1) 条赛道。可以修建经过第 (3,1,2,6) 条道路的赛道（从路口 (4) 到路口 (7)）， 则该赛道的长度为 (9 + 10 + 5 + 7 = 31)，为所有方案中的最大值。

样例输入 #2

9 3 
1 2 6 
2 3 3 
3 4 5 
4 5 10 
6 2 4 
7 2 9 
8 4 7 
9 4 4

样例输出 #2

15

【输入输出样例 #2 说明】

所有路口及适合于修建赛道的道路如下图所示：

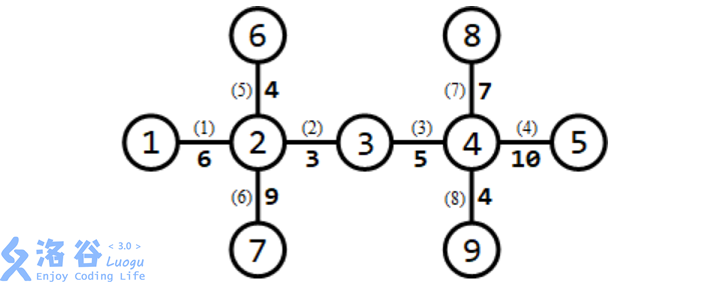
需要修建 $3 $条赛道。可以修建如下 $3 $条赛道：

1. 经过第 $1,6 $条道路的赛道（从路口 (1) 到路口$ 7$），长度为 (6 + 9 = 15)；
2. 经过第$ 5,2,3,8$ 条道路的赛道（从路口$ 6$ 到路口 (9)），长度为 (4 + 3 + 5 + 4 = 16)；
3. 经过第 (7,4) 条道路的赛道（从路口 (8) 到路口$ 5$），长度为 (7 + 10 = 17)。 长度最小的赛道长度为 (15)，为所有方案中的最大值。

数据规模与约定

所有测试数据的范围和特点如下表所示 :

测试点编号	(n)	(m)	(a_i=1)	(b_i=a_i+1)	分支不超过 (3)
(1)	(le 5)	(=1)	否	否	是
(2)	(le 10)	(le n-1)	否	是	是
(3)	(le 15)	(le n-1)	是	否	否
(4)	(le 10^3)	(=1)	否	否	是
(5)	(le 3 imes 10^4)	(=1)	是	否	否
(6)	(le 3 imes 10^4)	(=1)	否	否	否
(7)	(le 3 imes 10^4)	(le n-1)	是	否	否
(8)	(le 5 imes 10^4)	(le n-1)	是	否	否
(9)	(le 10^3)	(le n-1)	否	是	是
(10)	(le 3 imes 10^4)	(le n-1)	否	是	是
(11)	(le 5 imes 10^4)	(le n-1)	否	是	是
(12)	(le 50)	(le n-1)	否	否	是
(13)	(le 50)	(le n-1)	否	否	是
(14)	(le 200)	(le n-1)	否	否	是
(15)	(le 200)	(le n-1)	否	否	是
(16)	(le 10^3)	(le n-1)	否	否	是
(17)	(le 10^3)	(le n-1)	否	否	否
(18)	(le 3 imes 10^4)	(le n-1)	否	否	否
(19)	(le 3 imes 10^4)	(le n-1)	否	否	否
(20)	(le 5 imes 10^4)	(le n-1)	否	否	否

其中，「分支不超过 (3)」的含义为：每个路口至多有 (3) 条道路与其相连。

对于所有的数据，(2 le n le 5 imes 10^4, 1 le m le n − 1, 1 le a_i,b_i le n, 1 le l_i le 10^4)。

---

0x01 前言

使用知识点：树形dp，贪心，二分

这题其实并没有考察到超纲的知识点可我还是不会，但是在思维上非常妙。

所以如果是在考场上，还是建议先骗分。原题链接。

---

0x02 骗分

这道题骗分很好想a。

Part 1: 若 (m = 1) 则直接在树上跑直径即可。

// ans[x] 表示过 x 的最长路径。
// dp[x] 表示以 x 为端点的最长路径。
void Tree_Dp(int u) {
	for(int i = 0; i < mp[u].size(); i++) {
		int v = mp[u][i].v;
		int cost = mp[u][i].w;	
		if(vis[v])
			continue;
		vis[v] = true;
		Tree_Dp(v);
		ans[u] = Max(ans[u], dp[u] + dp[v] + cost);
		dp[u] = Max(dp[u], dp[v] + cost);
	}
}

Part 2: 若这是一条链，我们考虑二分答案。

原题目也就转换为给定一个序列，将其划分为 (m) 段，使得最小值最大。

那么贪心一下 (check) 函数即可。

// sum 表示当前段的当前状态的元素和了，cnt 表示分出了多少段。
// 因为 x 是表示最小值的最大值，所以我们在这里可以看作将整个序列分成 m 及以上个元素和大于 x 的段。
bool check(int x) {
	int sum = 0, cnt = 0;
	for(int i = 1; i < n; i++) {
		if(sum + road[i] < x) // 如果加上当前元素还小于，则将这个元素放在当前段中。
			sum += road[i];
		else { // 否则切换成下一个段，累加 cnt
			cnt++;
			sum = 0;
		} 
	}
	return cnt >= m;
}

Part 3: 若是一个菊花图，也可以贪心求出答案。

菊花图就好办嘛，因为是一个菊花图，所以每条赛道至多有2条边。

我们对于每条边，只需考虑如何最优的找到与之匹配的边即可，且满足最小值最大。

// 一定是从大到小取 m 条，这样才有价值最大。
// 对于第 i 条边，我们考虑取除这最大的 m 条边之外的对应边（最大中的第 i 边与除去 m 条最大边后的第i边配对。
// 如果取不到就只能这条边自成一条赛道。
bool cmp(int x, int y) {return x > y;}

sort(road + 1, road + n, cmp);
int ans = INF;
for(int i = 1; i <= m; i++) {
    int t = road[i] + (2 * m - i + 1 <= n - 1 ? road[2 * m - i + 1] : 0);
    ans = Min(ans, t);
}

Part 4: 当然，对于 Part 2，Part 3，我们需要先将所有的边拉出来，简单遍历不在赘述。

int road[MAXN], size = 0;
bool vis2[MAXN];

void Make_Road(int u) {
	for(int i = 0; i < mp[u].size(); i++) {
		int v = mp[u][i].v;
		int cost = mp[u][i].w;	
		if(vis2[v])
			continue;
		vis2[v] = true;
		Make_Road(v);
		road[++size] = cost;
	}
}

处理完这些特殊情况，你就会发现，你有55分了！！！

---

0x03 正解

前言中说到了，这是道树形dp，但其实不完全准确，这道题只是用了类似的更新思想。

首先，这道题肯定需要二分答案，于是我们考虑 (check())。

(check()) 完成的操作就是判断能否构成大于等于 (m) 条赛道，且所有赛道的最小长度的最大值大于等于 (mid)。

在 (check())，我们定义一个变量 (val)，(val) 在遍历完以 (v) 为根的子树后返回时，它表示在以 (v) 为根的子树，还没有构成赛道的最长链。

对于这个 (val)：（规定 (k) 表示当前枚举到的 (mid)，(cost) 表示我们枚举到的结点 (x) 与 (v) 连边的长度，(ans) 表示最后总共构成了多少条赛道。

• 如果 (val + cost geq k)，则就相当于这个 (val) 对应的链构成赛道了，直接累加 (ans)。
• 否则，我们就需要去判断了，如果能找到另外一条闲置的链与这条链构成赛道，那么依然可以累加 (ans)。

该如何去找呢？这种时候就应该贪一下。

对于一条闲置的长度为 (val_p) 的链 (p)，我们去找一条闲置的链，使得其长度大于等于 (k - val_p) 且是所有满足条件中长度最小的链。

这样就能尽可能多的去构成赛道。

如果能找到，就累加，否则这条链相当于就废掉了（意思是说这条链无法找到由它深度更小的那一个端点为终点的另外一条闲置的链去构成赛道。在这种情况下，因为我们要递归到上一层，所以无法再在后续操作中找到与这条链共端点的闲置的链了），继续回溯。

实现时运用了可重有序集合 (multiset) 以及迭代器的使用。如果有不了解的戳这里。

关键代码分析:

multiset<int> num[MAXN];
// num 里面存放的是所有当前闲置链的长度，即传上来的所有的 val。
int Ans = 0;
// Ans 表示总共可以构成多少条满足条件的赛道。

int dfs(int x, int fa, int k) {
	// dfs 返回的是val的值。
	num[x].clear(); // 清空。
	for(int i = 0; i < mp[x].size(); i++) {
		int v = mp[x][i].v;
		int cost = mp[x][i].w;
		if(v == fa)
			continue;
		int val = dfs(v, x, k) + cost; 
		if(val >= k) // 这条链自己可以构成赛道。
			Ans++;
		else // 反正，加入 multiset 方便查询配对。
			num[x].insert(val);
	}
	multiset<int>::iterator it;	// 迭代器。
	int res = 0; // 当前结点的 val 值。
	while(!num[x].empty()) { // 从长度最小的链开始配对。
		if(num[x].size() == 1) { 
			// 如果只有一个元素了，也就是说没有任何一条链可以和当前元素对应的链配对了，表示其为闲置，直接更新 res。
			res = Max(res, *num[x].begin());	
			break;		
		}
		it = num[x].lower_bound(k - *num[x].begin());
		// 找到长度最小的满足长度大于等于（k - 当前元素对应链长度）的闲置的链。
		// 你没看错，multiset 自带 lower_bound。
		// 注意 lower_bound 返回的是下标。
		// lower_bound 函数中如果找不到满足条件的数返回 num[x].end() 。
		if(it == num[x].begin() && num[x].count(*it) == 1) 
			it++;
		// 如果找到的链就是当前链，那么只能尝试去取稍大一点的下一条链（赘述一句：multiset 保证元素有序。
        if(it == num[x].end()) {
		// 如果无法配对，删除当前链，更新 res。
            res = Max(res, *num[x].begin());
            num[x].erase(num[x].find(*num[x].begin()));
        }
        else {
		// 配对成功，累加赛道构成个数，并在 multiset 中删除这条链和与它配对的链。
            num[x].erase(num[x].find(*it));
            num[x].erase(num[x].find(*num[x].begin()));
            Ans++;			
        }
	}
	return res;
}

0x04 完整代码

事实证明，判断完所有的特殊情况会快很多。（其实主要是菊花图卡时间。

所以还是贴个完整码吧，写的有些长，仅供参考。。。

#include <set>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

inline int Max(int x, int y) {return x > y ? x : y;}
inline int Min(int x, int y) {return x < y ? x : y;}

void read(int &x) {
    x = 0;
    int k = 1;
    char s = getchar();
    while (s < '0' || s > '9') {
        if (s == '-')
            k = -1;
        s = getchar();
    }
    while (s >= '0' && s <= '9') {
        x = (x << 3) + (x << 1) + s - '0';
        s = getchar();
    }
    x *= k;
    return;
}

void write(int x) {
    if(x < 0) {
    	putchar('-');
		x = -x;
    }
    if(x > 9)
		write(x / 10);
    putchar(x % 10 + '0');
}

const int MAXN = 5 * 1e4 + 5;
const int INF = 0x3f3f3f3f;
struct edge {
	int v, w;
	edge() {}
	edge(int V, int W) {
		v = V;
		w = W;
	}
};
vector<edge> mp[MAXN];
int n, m;

void Add_Edge(int u, int v, int w) {
	mp[u].push_back(edge(v, w));
	mp[v].push_back(edge(u, w));
}

int ans[MAXN], dp[MAXN];
bool vis[MAXN];
void Tree_Dp(int u) {
	for(int i = 0; i < mp[u].size(); i++) {
		int v = mp[u][i].v;
		int cost = mp[u][i].w;	
		if(vis[v])
			continue;
		vis[v] = true;
		Tree_Dp(v);
		ans[u] = Max(ans[u], dp[u] + dp[v] + cost);
		dp[u] = Max(dp[u], dp[v] + cost);
	}
}

int road[MAXN], size = 0;
bool vis2[MAXN];

void Make_Road(int u) {
	for(int i = 0; i < mp[u].size(); i++) {
		int v = mp[u][i].v;
		int cost = mp[u][i].w;	
		if(vis2[v])
			continue;
		vis2[v] = true;
		Make_Road(v);
		road[++size] = cost;
	}
}

bool check(int x) {
	int sum = 0, cnt = 0;
	for(int i = 1; i < n; i++) {
		if(sum + road[i] < x) 
			sum += road[i];
		else {
			cnt++;
			sum = 0;
		} 
	}
	return cnt >= m;
}

bool cmp(int x, int y) {return x > y;}

multiset<int> num[MAXN];
int Ans = 0;

int dfs(int x, int fa, int k) {
	num[x].clear();
	int val = 0;
	for(int i = 0; i < mp[x].size(); i++) {
		int v = mp[x][i].v;
		int cost = mp[x][i].w;
		if(v == fa)
			continue;
		val = dfs(v, x, k) + cost;
		if(val >= k)
			Ans++;
		else 
			num[x].insert(val);
	}
	multiset<int>::iterator it;
	int res = 0;
	while(!num[x].empty()) {
		if(num[x].size() == 1) {
			res = Max(res, *num[x].begin());	
			break;		
		}
		it = num[x].lower_bound(k - *num[x].begin());
		if(it == num[x].begin() && num[x].count(*it) == 1) 
			it++;
        if(it == num[x].end()) {
            res = Max(res, *num[x].begin());
            num[x].erase(num[x].find(*num[x].begin()));
        }
        else {
            num[x].erase(num[x].find(*it));
            num[x].erase(num[x].find(*num[x].begin()));
			Ans++;
        }
	}
	return res;
}

bool Check(int k) {
	Ans = 0;
	dfs(1, -1, k);
	if(Ans >= m)
		return true;
	return false;
}

int main() {
//	freopen("track.in", "r", stdin);
//	freopen("track.out", "w", stdout);
	read(n); read(m);
	int sum = 0;
	bool flag1 = true, flag2 = true;
	for(int i = 1; i < n; i++) {
		int u, v, w;
		read(u); read(v); read(w);
		if(v != u + 1)
			flag1 = false;
		if(u != 1)
			flag2 = false;
		Add_Edge(u, v, w);
		sum += w;
	}
	if(m == 1) {
		vis[1] = true;
		Tree_Dp(1);
		int res = 0;
		for(int i = 1; i <= n; i++) 
			res = Max(res, ans[i]);			
		write(res);
		return 0;
	}
	if(flag1) {
		vis2[1] = true;
		Make_Road(1);
		int l = 1, r = sum, ans = 0;
		while(l <= r) {
			int mid = (l + r) >> 1;
			if(check(mid)) {
				l = mid + 1;
				ans = mid;		
			}
			else
				r = mid - 1;
		}
		write(ans);
		return 0;
	}
	if(flag2) {
		vis[1] = true;
		Make_Road(1);
		sort(road + 1, road + n, cmp);
		int mi = INF;
		for(int i = 1; i <= m; i++) {
			int t = road[i] + (2 * m - i + 1 <= n - 1 ? road[2 * m - i + 1] : 0);
			mi = Min(mi, t);
		}
		write(mi);
		return 0;
	}
	int l = 1, r = sum, ans = 0;
	while(l <= r) {
		int mid = (l + r) >> 1;
		if(Check(mid)) {
			l = mid + 1;	
			ans = mid;		
		}
		else
			r = mid - 1;
	}
	write(ans);	
	return 0;
}