一、最大间隔分类器
1. 函数间隔:(γ^{i} = y^{i}(w^{T} x + b)),
- 改变w和b的量级,对分类结果不会产生任何影响,但是会改变函数间隔的大小。因此,直接对函数间隔求最大值是没有任何意义的。因为可以通过任意改变w、b的量级,使得函数间隔任意大。
Q1: 函数间隔的式子中,(w^{T} x + b)的结果在几何意义上代表什么?或则假设有两个样点(x_i)和(x_j),如果(w^{T} x _i+ b)的值大于(w^{T} x_j + b),是否表明(x_i)比(x_j)距离分类器更远,有更大的确信度分类正确?
A1: 第一问: 结果会随参数的量级的改变而改变。
第二问:是的。
Q2: 假设有一个已经计算好参数的分类器,那么在函数间隔中,可以确保(w^(T)x + b)的符号和(y^(i))的符号是一致的,即确保分类的正确性。此外,我们都知道当一个样点距离分类器越远的时候,则这个样点就有越大的确信度分类正确,但是在函数间隔中,(w^(T)x + b)的值是否也代表了这种确信度?
A2: 显然,(w^{T} x + b)并不能代表这种确信度。首先当我们任意改变w、b的量级时,分类器的方向和位置并不会发生任何改变,但是(w^{T} x + b)的值却会发生变化,因此无法表示分类正确的确信度。
2. 几何间隔:在线性分类算法中,训练数据和拟合出来的直线之间的距离。
- 在logistic regression中,当(Theta^{x}x >> 0)时,可认为样本有很大的概率和可信度被预测为1,反之亦成立。所以把这条结论应用到图像上时,最直观的解释就是数据到直线间的距离尽可能远。所以一个较好的拟合结果,就是确保直线和大部分训练数据的距离都尽可能远,即处于中间。
- 改变w和b的量级,对几何间隔没有任何影响。且,通过||w||,可以得到几何间隔和函数间隔之间的关系。
Q: 最大间隔分类器的目标就是要最大化几何间隔,那为什么要额外引入函数间隔?
A: 函数间隔和几何间隔可以通过||w||进行转换,且函数间隔的量级会随参数的量级的改变而改变,这为之后最大间隔分类器的问题优化以及公式形式的转变提供了很好的帮助。
二、拉格朗日对偶
拉格朗日对偶的重要作用是将w的计算提前并消除w
三、核函数
对于某个问题,如何确定具体使用的核函数形式?如何确保使用的这个核函数是可行的?
- Linear核:主要用于线性可分的情形。参数少,速度快,对于一般数据,分类效果已经很理想了。
- RBF核:主要用于线性不可分的情形。参数多,分类结果非常依赖于参数。有很多人是通过训练数据的交叉验证来寻找合适的参数,不过这个过程比较耗时。我个人的体会是:使用libsvm,默认参数,RBF核比Linear核效果稍差。通过进行大量参数的尝试,一般能找到比linear核更好的效果。至于到底该采用哪种核,要根据具体问题,有的数据是线性可分的,有的不可分,需要多尝试不同核不同参数。如果特征的提取的好,包含的信息量足够大,很多问题都是线性可分的。当然,如果有足够的时间去寻找RBF核参数,应该能达到更好的效果。
四、L1 norm软间隔问题
-
参数C的作用?
C比较大的时候代表犯错越少越好,C比较小的时候代表找到的w越短越好,也就是在对的数据上的间隔越宽越好。
五、SVM完整推导过程
对于支持向量机,其主要作用的还是取决于距离线性平面最近的那几个点(亦称为支持向量),算法考虑了每一个支持向量,这也导致了当添加了一个额外的极端值之后,原本表现好的线性平面可能会受到影响,得到一个几何间隔更小的线性平面。
对于分类问题,假设数据是线性可分隔的,即可以找到一个超平面划分不同类的数据,那么某一样点距离超平面的距离越远,则分类正确的可信度越高。因此,可以证明,当超平面位于不同类数据的中间时,即最大化所有样本距离超平面的最小值,可得到最优间隔分类器。
函数间隔可以表示点到超平面的间隔。但是在函数间隔中,当参数w和b成线性变换时,分类结果不变,但是函数间隔的值却会改变。由此引入了一个新的概念:几何间隔。在几何间隔中,参数w和b线性变换时,几何间隔的值都不会发生改变。在通过固定间隔的值为1,去掉一些影响问题求解的参数后,整个问题变转化为:
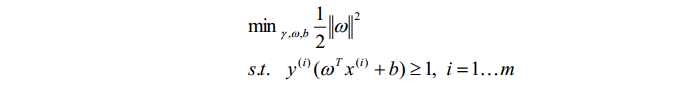
为了求解这个问题,引入了拉格朗日对偶问题。通过对偶问题的求解以及KKT条件的限制,得到:

因此,原先的问题便转化为:
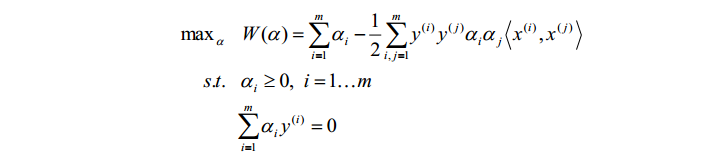
在低维度下,数据可能存在线性不可分的情况,而将特征映射到高维空间后,往往就可分了。因此,通过仿射函数将特征映射到高维空间。但此时又出现一个新的问题:在这个公式里,需要计算特征向量的内积,当特征向量非常多时且映射到高维空间后,直接计算所需要的时间复杂度O(n)很可能为(n^{2})甚至更大。因此引入了核函数,可以证明,核函数可以化为两个仿射函数的乘积,从而通过直接计算核函数,而不是一一计算仿射函数,使得计算的复杂度缩小到O(n)。
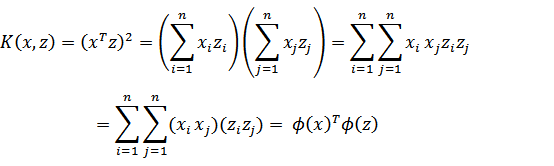
核函数通过将低维数据映射到高维,在高维空间用超平面将数据分隔开来,可以解决原数据线性不可分隔的情况。
不过上述这个模型对于噪声点还是很敏感的,几个数据的变化都会导致整个超平面发生变化,如下图所示:
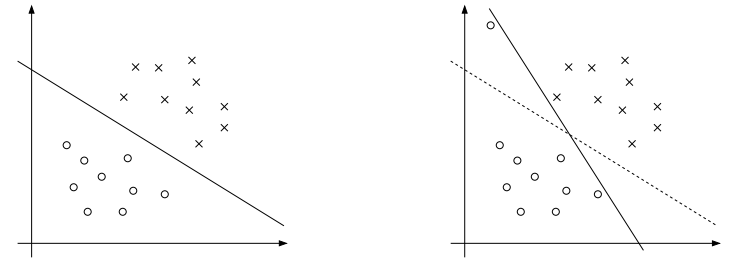
因此,为了避免这种情况的出现,在模型里添加了惩罚项C和$xi $,其中C比较大的时候代表犯错越少越好,C比较小的时候代表找到的w越短越好,也就是在对的数据上的间隔越宽越好。最终模型如下所示:
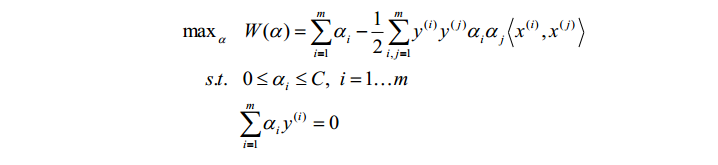
到这里,整个问题就转化成对拉格朗日参数(alpha)的优化求解,当(alpha)求解出来之后,w和b随之得解,于是便找到了我们所想要的超平面。那么如何对参数(alpha)进行求解呢?可以采用坐标上升法——即反复通过固定其他参数为固定值,对特定(alpha^{i})进行优化,来优化求解所有的(alpha)值。但是在SVM中,因为条件 的限制,无法只对单一参数进行优化,因此导出了SMO算法。在SMO算法中,每次对两个不同的(alpha^{i})和(alpha^{j})同时进行优化,增加其中一个(alpha)的时候,对另一个值减少相同的量,以此满足限制条件 。对于SMO算法,每一次循环(alpha^{i})和(alpha^{j})的选择有一个启发式选择规则,即每次选择改变步长最大的j,可以使得算法更快得收敛。
至此,SVM模型中,所需要的所有参数都得以求解,我们得到了一个最优间隔分类器,将新的测试数据代入计算,通过结果大于0或则小于0,便可完成分类功能。
六、coursera课程上的SVM推导思路
在之前的分类问题中采用的是logistic回归的方法,在logistic回归中,只要求分类器能够正确得分类不同的样本,使得对应正样本函数输出( heta^(T)X>=0),且对应负样本函数输出( heta^(T)X<0)即可,而对于分类正确的确信度没有太大的要求。然而在SVM中,不仅仅要求找到分类器,且要尽可能使得对于每一个样本,分类器都有较大的概率分类正确,即最大化样本距离分类器的间距。
在SVM中,首先用两条直线近似logistic回归中的代价函数,然后用参数C替代正则化常数(lambda),可以证明,这个推导过程是近似等价的。接着将参数C设置为很大的一个数(例如1000000),因此在最小化代价函数过程中,公式的第一项就要尽可能为0,等同于对于所有的正样本函数输出$ heta(T)X>=$1,且对应负样本函数输出$ heta(T)X<=-1$,由此推导出SVM的目标方程。
参数C设置很大的时候,等同于正则化常数(lambda)变小,此时的话函数易于过拟合,即函数对于样本中的异常点会异常敏感,一个样本的变动都会使得分类器改变,这显然不是我们想要的。因此,我们不能将C设置得过大,亦不能将C设置过小。(C类似于上面“四、L1 norm软间隔问题”中参数C的作用)
Q:为什么支持向量机是一个最大间距分类器?(为什么如上的目标方程可以得到最大间距分类器?)
A:SVM试图极大化(p^(i))的范数,即训练样本到决策边界的举例。(参考笔记196-200页部分)
为什么?
下面是一些普遍使用的准则:
n 为特征数, m 为训练样本数。
(1)如果相较于 m 而言, n 要大许多,即训练集数据量不够支持我们训练一个复杂的非
线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
(2)如果 n 较小,而且 m 大小中等,例如 n 在 1-1000 之间,而 m 在 10-10000 之间,
使用高斯核函数的支持向量机。
(3)如果 n 较小,而 m 较大,例如 n 在 1-1000 之间,而 m 大于 50000,则使用支持向量
机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向
量机。