题目描述
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个N 行M 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第1 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第N 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入输出格式
输入格式:
输入文件的每行中两个数之间用一个空格隔开。输入的第一行是两个正整数N 和M,表示矩形的规模。接下来N 行,每行M 个正整数,依次代表每座城市的海拔高度。
输出格式:
输出有两行。如果能满足要求,输出的第一行是整数1,第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数0,第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
输入输出样例
输入样例#1:
【输入样例1】 2 5 9 1 5 4 3 8 7 6 1 2 【输入样例2】 3 6 8 4 5 6 4 4 7 3 4 3 3 3 3 2 2 1 1 2
输出样例#1:
【输出样例1】 1 1 【输出样例2】 1 3
说明
【样例1 说明】
只需要在海拔为9 的那座城市中建造蓄水厂,即可满足要求。
【样例2 说明】
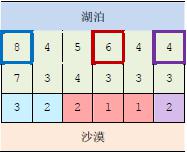
上图中,在3 个粗线框出的城市中建造蓄水厂,可以满足要求。以这3 个蓄水厂为源头
在干旱区中建造的输水站分别用3 种颜色标出。当然,建造方法可能不唯一。
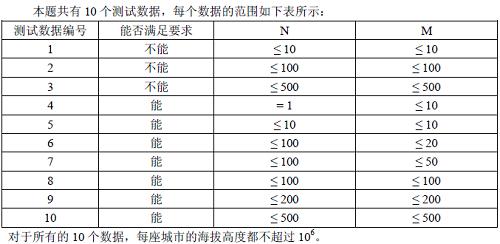
【数据范围】
这是一个没过,但没找出问题的程序。
#include<iostream> #include<queue> #include<cstdio> #include<algorithm> #include<math.h> #include<string.h> using namespace std; int n,m; int map[510][510],f[510]; int ans1; int X[300000],Y[300000],color[510][510]; struct node{ int L,R; }a[510]; int l,r; void push(int x,int y,int cnt) { if(x<1||x>m||y>n||y<1||color[x][y]==cnt) return ; if(y==n) a[cnt].L=min(a[cnt].L,x),a[cnt].R=max(a[cnt].R,x); X[++r]=x,Y[r]=y; color[x][y]=cnt; return; } void bfs(int x,int y,int cnt) { l=0,r=1; a[cnt].L=999999,a[cnt].R=0; X[1]=x,Y[1]=y; color[x][y]=cnt; while(l<=r) { x=X[++l];y=Y[l]; if(map[x][y]>map[x+1][y]) push(x+1,y,cnt); if(map[x][y]>map[x-1][y]) push(x-1,y,cnt); if(map[x][y]>map[x][y+1]) push(x,y+1,cnt); if(map[x][y]>map[x][y-1]) push(x,y-1,cnt); } return ; } bool cmp(node x,node y) { if(x.L==y.L) return x.R>y.R; return x.L<y.L; } int main() { scanf("%d%d",&n,&m); for(int j=1;j<=n;j++) for(int i=1;i<=m;i++) scanf("%d",&map[i][j]); for(int i=1;i<=m;i++) bfs(i,1,i); int tot=0; for(int i=1;i<=m;i++) if(!color[i][n]) tot++; if(tot) { printf("0 "); printf("%d",tot); return 0; } /// sort(a+1,a+1+m,cmp); f[0] = 0; for (int i = 1;i <= m;i ++) { f[i] = 9999999; for (int j = 1;j <= m;j ++) if (i >= a[j].L && i <= a[j].R) f[i] = min(f[i],f[a[j].L - 1] + 1); } cout<<'1'<<endl << f[m]; return 0; }
横纵坐标混了
#include<iostream> #include<queue> #include<cstdio> #include<algorithm> #include<math.h> #include<string.h> using namespace std; int n,m; int map[510][510],f[510]; int ans1; int X[300000],Y[300000],color[510][510]; struct node{ int L,R; }a[510]; int l,r; bool b[510][510]; int dx[4]={0,1,0,-1},dy[4]= {1,0,-1,0},cnt; void bfs() { l=0,r=0;int x, y,xx,yy; for(int i=1;i<=m;i++) { b[1][i]=1; X[++r]=1; Y[r]=i; } while(l<r) { x=X[++l],y=Y[l]; for(int i=0;i<4;i++) { xx=x+dx[i],yy=y+dy[i]; if (xx > n || xx < 1 || yy > m || yy < 1) continue; if (map[x][y] <= map[xx][yy]) continue; if(b[xx][yy]) continue; b[xx][yy]=1; X[++r]=xx,Y[r]=yy; } } return ; } void dfs(int x,int y) { b[x][y]=1; if(x==n) { a[cnt].L=min(a[cnt].L,y); a[cnt].R=max(a[cnt].R,y); } int xx,yy; for(int i=0;i<4;i++) { xx=x+dx[i]; yy=y+dy[i]; if (xx > n || xx < 1 || yy > m || yy < 1) continue; if (map[x][y] <= map[xx][yy]) continue; if (!b[xx][yy]) dfs(xx,yy); } } bool cmp(node x,node y) { if(x.L==y.L) return x.R>y.R; return x.L<y.L; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&map[i][j]); bfs(); int tot=0; for(int i=1;i<=m;i++) if(!b[n][i]) tot++; if(tot) { printf("0 "); printf("%d",tot); return 0; } for(int i=1;i<=m;i++) { memset(b,0,sizeof(b)); a[i].L=99999; a[i].R=0; cnt=i; dfs(1,i); } f[0] = 0; for (int i = 1;i <= m;i ++) { f[i] = 9999999; for (int j = 1;j <= m;j ++) if (i >= a[j].L && i <= a[j].R) f[i] = min(f[i],f[a[j].L - 1] + 1); } cout<<'1'<<endl << f[m]; return 0; }