概述
在高维情形下出现的数据样本稀疏、距离计算困难等问题,是所有机器学习方法共同面临的严重障碍,被称为维数灾难。
缓解维数灾难的一个重要途径是降维,亦称为维数约简,即通过某种数学变换将原始高维属性空间转变为一个低维子空间。在这个子空间中样本密度大幅提高,距离计算也更为容易。
低维嵌入
人们观测或者收集到的数据样本虽是高维的,但与学习任务密切相关的仅是某个低维分布,即高维空间中的一个低维“嵌入”。下面介绍一种经典降维方法:多维缩放(MDS)。
若要求原始空间中样本之间的距离在低维空间中得以保持,即多维缩放(Multiple Dimensional Scaling,MDS)。
1、MDS推导:
问题描述:

问题转换:
![]()

![]()
如何求B:
由 和
和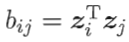
得


2、算法总结:

PCA和KPCA
1、主成分分析(Principal Component Analysis,PCA)
PCA请参考这篇大神博客(写的太好了,致敬致敬):http://blog.codinglabs.org/articles/pca-tutorial.html?tdsourcetag=s_pcqq_aiomsg
2、核主成分分析(Kernel Principal Component Analysis, KPCA)
假设中心化后的样本集合X(d*N,N个样本,维数d维,样本”按列排列“),现将X映射到高维空间,得到
回顾PCA,其协方差矩阵本是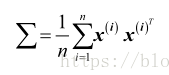
通过高维映射后,协方差矩阵变为
令
直接对K按PCA剩余步骤求解即可。
流形学习
流形学习是一种借鉴了拓扑流形概念的降维方法。“流形”是局部与欧氏空间同胚的空间,在局部具有欧氏空间的特性。
若低维流形嵌入到高维空间,则数据样本在高维空间上虽然看起来复杂,但是在局部仍然具有欧式空间的性质,因此可以容易的在局部建立降维映射关系。随后再将局部推广到全局。
下面介绍两个著名的流形学习方法
1、等度量映射(IsometricMapping,Isomap)
思想:
利用流形在局部上与欧氏空间同胚这个性质,对每个点基于欧氏距离找出其近邻点,然后就能建立一个近邻连接图,图中近邻点之间存在连接,而非近邻点之间不存在连接,于是,计算两点之间测地线距离的问题就转变为计算近邻连接图上两点之间的最短路径问题,在得到任意两点的距离之后,就可通过 MDS 方法来获得样本点在低维空间中的坐标,实现降维。
对近邻图的构建有两种做法:
一种是指定近邻点个数,如欧式距离最近的k个点为近邻点,称为k近邻图;另一种是指定距离阈值 ,距离小于阈值的点被认为是近邻点,称为近邻图。两种方法均有不足,若近邻范围指定过大,则距离很远的点可能被误认为是近邻,出现短路问题;近邻范围指定过小,则图中有些区域可能与其他区域不存在连接,出现断路问题。断路和短路都会给后续的最短路径计算造成误导。
如何求最短路径:
在计算两点间的最短路径后,可采用著名的Dikstra算法或Floyd 算法,推荐博客:
Dijkstra算法:https://blog.csdn.net/qq_39521554/article/details/79333690
Floyd 算法:https://www.cnblogs.com/wangyuliang/p/9216365.html
对于新样本,如何将其映射到低维空间:
Isomap得到了训练样本在低维空间的坐标,常用解决方案是,将训练样本的高维空间坐标作为输入、低维空间坐标作为输出,训练一个回归学习器来对新样本的低维空间坐标进行预测。文中说不是最佳之法,却也没有更好的。
最终算法流程:

2、局部线性嵌入(Locally Linear Embedding,LLE)
与Isomap试图保持近邻样本之间的距离不同,LLE试图保持邻域内样本间的线性关系。
推荐参考博客:https://www.cnblogs.com/pinard/p/6266408.html?utm_source=itdadao&utm_medium=referral
思想:

计算步骤:
第一步,求权重

第二步,求降维后的空间坐标


最终算法流程:

度量学习
前面讨论的降维方法都试图将原空间投影到一个合适的低维空间中,接着在低维空间进行学习任务从而产生较好的性能。事实上,不管高维空间还是低维空间都潜在对应着一个距离度量,而寻找合适的空间,实质上就是在寻找一个合适的距离度量,那可不可以直接学习出一个距离度量来等效降维呢?这便是度量学习的初衷。
首先要学习出距离度量必须先定义一个合适的距离度量形式。对两个样本xi与xj,它们之间的平方欧式距离为:
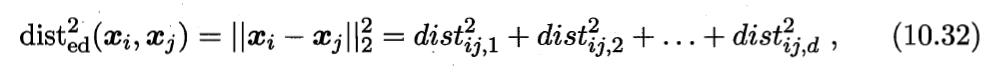
若各个属性重要程度不一样即都有一个权重,则得到加权的平方欧式距离:

此时各个属性之间都是相互独立无关的,但现实中往往会存在属性之间有关联的情形,例如:身高和体重,一般人越高,体重也会重一些,他们之间存在较大的相关性。这样计算距离就不能分属性单独计算,于是就引入经典的马氏距离(Mahalanobis distance):

标准的马氏距离中M是协方差矩阵的逆,马氏距离是一种考虑属性之间相关性且尺度无关(即无须去量纲)的距离度量。
矩阵M也称为“度量矩阵”,为保证距离度量的非负性与对称性,M必须为(半)正定对称矩阵,这样就为度量学习定义好了距离度量的形式,换句话说:度量学习便是对度量矩阵进行学习。
现在来回想一下前面我们接触的机器学习不难发现:机器学习算法几乎都是在优化目标函数,从而求解目标函数中的参数。同样对于度量学习,也需要设置一个优化目标。经典的算法有近邻成分分析(Neighbourhood Component Analysis,NCA),这里不再展开。