一、直接选择排序
#include <iostream> using namespace std; void print_array(int a[], int n) { for(int i = 0; i < n; i++) cout << a[i] << " " ; cout << endl; } void Swap(int &a, int &b) { if(a != b) { a ^= b; b ^= a; a ^= b; } } void select_direct(int a[], int n) { for(int i = 0; i < n; i++) { int middle = i; for(int j = i+1; j < n; j++) { if(a[middle] >= a[j]) { middle = j; } } Swap(a[middle],a[i]); } } int main() { int a[] = {5,4,9,8,2,7,0,1,6,3}; cout << "before sort:"; print_array(a, 10); select_direct(a, 10); cout << "after sort :"; print_array(a, 10); return 0; }
说明:
直接选择排序基本思想:第一次从a[0]~a[n-1]中选出最小值,与a[0]交换;第二次从a[1]~a[n-1]选出最小值,与a[1]交换;......第n-1次从a[n-2]~a[n-1]选出最小值,与a[n-2]交换,总共n-1次得到有序序列。
二、堆排序
(参考:
https://www.cnblogs.com/JVxie/p/4859889.html (这篇通俗易懂,但是弹出部分讲的不清晰,有代码实现)
https://www.jianshu.com/p/6b526aa481b1 (这篇比上篇讲的清晰很多,没有代码实现)
)
堆概念:堆是用数组实现的二叉树,它没有父指针和子指针。可以被视为一个完全二叉树。
那什么是完全二叉树呢?——若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
现在画两种完全二叉树:根据节点的序号不同,父节点和子节点的序号关系也会不同。根据对应关系,存储树就只需要一个简单的数组,不需要额外的空间了。
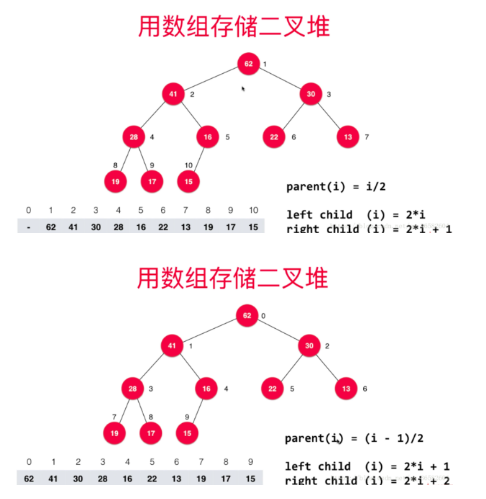
堆分为两种类型:最大堆和最小堆。在最大堆中,父节点的值比每一个子节点的值都要大。在最小堆中,父节点的值比每一个子节点的值都要小。上图的堆属于最大堆。这种最大堆和最小堆的属性非常有用,因为堆常常被当做优先队列使用,因为可以快速的访问到“最重要”的元素。
那么,如果一个堆不是最大/小堆,我们该如何去维护?
有以下几个操作:
- 上浮 shift_up
- 下沉 shift_down
- 插入 push
- 弹出 pop
- 取顶 top
- 堆排序 heap_sort
例子图示:
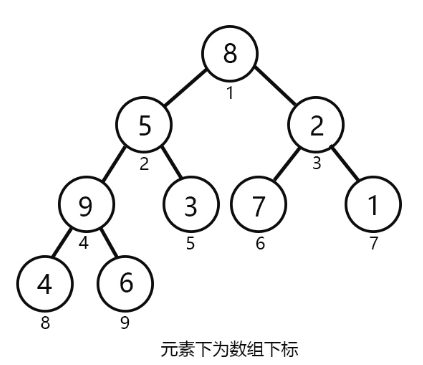
如果要将上图的树堆化(Heapify)成最小堆。可以看出:根节点1(value = 8)的子节点3(value = 2)比根节点1小,所以应该交换节点3和节点1。但是节点7(value = 1)的值更小,这时候我们是无法直接和根节点交换的,那我们就需要一个操作来实现这个交换过程,那就是上浮 shift_up。
1.上浮 shift_up 操作过程如下:
从当前结点开始,和它的父节点比较,若是比父亲节点小,就交换,然后将当前节点下标更新为原父亲节点下标;否则退出。
模拟操作图示:
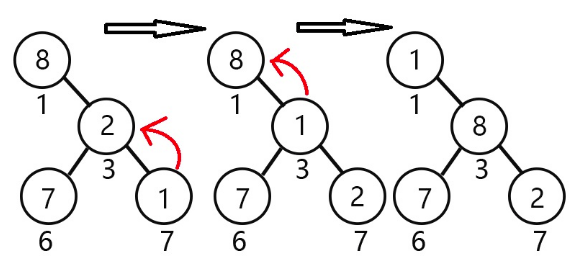
伪代码如下:
Shift_up( i ) { while( i / 2 >= 1) { if( 堆数组名[ i ] < 堆数组名[ i/2 ] ) { swap( 堆数组名[ i ] , 堆数组名[ i/2 ]) ; i = i / 2; } else break; }
这样,(value = 1)的节点就到了根节点1。但是还有一个问题:节点3(value = 8)比子节点6(value = 7)和子节点7(value = 2)都大,它需要和子节点交换,但是应该和哪一个子节点交换呢?答案是更小的那个。
2.所以就有了下沉操作 shift_down:
让当前结点的左右子节点(如果有的话)作比较,哪个比较小就和它交换,并更新当前节点的下标为被交换的子节点下标,否则退出。
模拟操作图示:
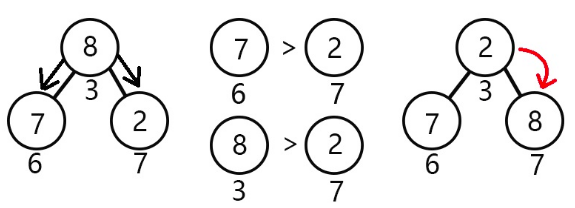
伪代码如下:
Shift_down( i , n ) //n表示当前有n个节点 { while( i * 2 <= n) //存在左节点 { T = i * 2 ; if( T + 1 <= n && 堆数组名[ T + 1 ] < 堆数组名[ T ]) //存在右节点 && 右节点 < 左节点 T++; if( 堆数组名[ i ] < 堆数组名[ T ] ) { swap( 堆数组名[ i ] , 堆数组名[ T ] ); i = T; } else break; }
3.插入 push 操作:在数组的最后一个插入。如果要维护树的结构,插入后要有上浮 shift_up 操作。
(例子参考 https://www.jianshu.com/p/6b526aa481b1)
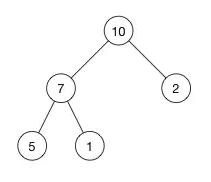
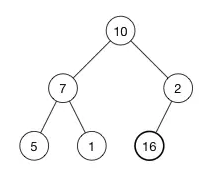
该堆的数组是:{10, 7, 2, 5, 1},现在将16插入到堆中,数组变成{10, 7, 2, 5, 1, 16},对应的堆变成右图。(该例为最大堆)
现在需要交换16和2,然后交换16和10,使得插入的节点(value = 16)比父节点小或者到达根节点。这就是上浮 shift_up 操作。
最后得到堆:
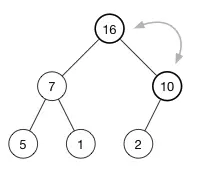
4.弹出 pop 操作:弹出堆顶元素,但是弹出后仍然需要维护堆的属性(最大堆/最小堆)。那么此时该怎么做呢?
具体做法:让根节点元素和尾节点进行交换,然后让现在的根元素下沉就可以了!
伪代码:
Pop ( x ) { swap( 堆数组名[1] , 堆数组名[ n ] ); n--; //这一步很关键 Shift_down( 1 ); }
5.取顶 top 操作:直接返回数组下标[1]的元素。
注意判断堆内是否还有元素。
6.堆排序 heap_sort 操作:开一个新的数组,每次取堆顶元素放入,然后把堆顶元素弹出。
伪代码:
Heap_sort( a[] ) { k=0; while( size > 0 ) { k++; a[ k ] = top(); pop(); } }
堆排序的时间复杂度是O(nlogn)理论上是十分稳定的,但是对于我们来说并没有什么卵用。
我们要排序的话,直接使用快排即可,时间更快,用堆排还需要O(2*n)的空间。这也是为什么我说堆的操作时间复杂度在O(1)~O(logn)。
讲完到这里,堆也基本介绍完了,那么它有什么用呢??
举个粒子,比如当我们每次都要取某一些元素的最小值,而取出来操作后要再放回去,重复做这样的事情。
我们若是用快排的话,最坏的情况需要O(q*n^2),而若是堆,仅需要O(q*logn),时间复杂度瞬间低了不少。
上述源码可参考:https://www.cnblogs.com/JVxie/p/4859889.html
另一个代码实现:
//这里序号是从0开始的,所以left=2i + 1; right = left + 1; parent = (i-1)/2 #include <iostream> using namespace std; void PrintArray(int a[], int n) { for(int i = 0; i < n; i++) cout << a[i] << " " ; cout << endl; } //构建最大堆,保证堆顶元素为最大 void MaxHeapify(int a[], int i, int size) { int l = 2*i+1, r = l + 1; int largest = 0; if((l < size) && (a[l] > a[i])) largest = l; else largest = i; if((r < size) && (a[r] > a[largest])) largest = r; if(largest != i) { int tmp = a[i]; a[i] = a[largest]; a[largest] = tmp; //cout << "exchange" <<endl; //PrintArray(a, size); MaxHeapify(a, largest, size); } //cout << "MaxHeapify" <<endl; //PrintArray(a, size); } //建堆:从i=(size-1)/2开始,调用MaxHeapify 直到i=0 void BuildMaxHeap(int a[], int size) { for(int i = (size-1) / 2; i >= 0; i--) { MaxHeapify(a, i, size); } } void HeapSort(int a[], int size) { BuildMaxHeap(a, size); cout << "build over:" << endl; PrintArray(a, size); int len = size; for(int i = size-1; i > 0; i--) { int tmp = a[i]; a[i] = a[0]; a[0] = tmp; len--; MaxHeapify(a, 0, len); } } int main() { int a[100] = {1,2,3,4,5,6,7,8,9}; int size=9; cout << "input :" << endl; PrintArray(a, size); HeapSort(a, size); cout << "sort over :" << endl; PrintArray(a, size); return 0; }