你还真信了
丢链接
这筛对积性函数的要求不同于杜教筛,只消函数在自变量为质数或质数整数幂时是一个低阶多项式即可。以下n<=1e11。
首先有一个性质:1~n的每个数,大于$sqrt{n}$的质因子只有一个。根据是否有大于$sqrt{n}$的质因子,再根据他是积性函数,得
$sum_{i=1}^nf(i)=sum_{i=1}^{n}[i has no prime greater than sqrt{n}]f(i)(1+sum_{i=sqrt{n}}^{left lfloor frac{n}{i} ight floor}[i is prime]f(i))$
好的!来观察他。首先$sum_{i=1}^{sqrt{n}}[i has no prime greater than sqrt{n}]$是可以线性筛的。
于是我们就差两部分:Part1:$sum_{i=sqrt{n}}^{left lfloor frac{n}{i} ight floor}[i is prime]f(i)$,Part2:$sum_{i=sqrt{n}}^n[i has no prime greater than sqrt{n}]f(i)$,并希望用$leq sqrt{n}$的质数来处理他们。
Part1:$g(i,j)$--$[1,j]$中与前$i$个质数互质的数的k次幂和。有递推式$g(i,j)=g(i-1,j)-p_i^kg(i-1,left lfloor frac{j}{p_i} ight floor)$。直接算的复杂度是$frac{n}{log(n)}$。
注意到$p_{i+1}>j$时$g(i,j)=1$,紧接着$p_i>left lfloor frac{j}{p_i} ight floor$即$p_i^2>j$时$g(i-1,left lfloor frac{j}{p_i} ight floor)=1$,因此$g(i,j)=g(i-1,j)-p_i^k$。
也就是说算到$p_i^2>j$时就不必再算了,后面要用某个$g(i,j)$时,若$p_{i+1}>j$则$g(i,j)=1$,否则用$g(i0_j,j)$减去一段$p_i^k$即可,其中$i0_j$表示最慢枚举到$j$的$i$。
Part2:$h(i,j)$--$[1,j]$中用前$i$个质数凑起来的数的$f$值的和。有$h(i,j)=h(i-1,j)+sum_{c=1}^{p_i^c<=j}f(p_i^c)h(i-1,left lfloor frac{j}{p_i^c} ight floor)$
然而这里没有上面那个用平方来卡$j$上限的性质!!咋整!!
反过来。把前$i$个改成后$i$个,注意是$leq sqrt{n}$的后$i$个。递推式同理。但!
$p_i>j$时$h(i,j)=1$,$p_i^2>j$时用后$i-1$个质数凑得$leq j$的部分只有1,因此$h(i,j)=h(i-1,j)+f(p_i)$。棒!用类似方法解决。
注意$h$实际上回答了$sum_{i=1}^{n}[i has no prime greater than sqrt{n}]f(i)$,因此最后加上即可,括号里那个1就不必理了。然后$g$中都是包含1的,但是我不要,因此在算答案的时候记得-1。
以下是那道万年不变的例题的代码。

1 //#include<iostream> 2 #include<cstring> 3 #include<cstdlib> 4 #include<cstdio> 5 //#include<map> 6 #include<math.h> 7 //#include<time.h> 8 //#include<complex> 9 #include<algorithm> 10 using namespace std; 11 12 #define LL long long 13 int T; LL n; 14 int m=320000; 15 #define maxn 640011 16 LL prime[maxn],f[maxn],sf[maxn],s[maxn],i0[maxn],who[maxn],g[maxn],ff[maxn],mi[maxn],ci[maxn]; 17 int lp,lw; bool notprime[maxn]; 18 19 #define maxh 1000007 20 struct Hash 21 { 22 int first[maxh],le; struct Edge{LL to,v; int next;}edge[maxn]; 23 void clear(LL n) {le=2; for (LL i=1;i<=n;i=n/(n/i)+1) first[n/i%maxh]=0;} 24 void insert(LL x,LL y) {int z=x%maxh; Edge &e=edge[le]; e.to=x; e.v=y; e.next=first[z]; first[z]=le++;} 25 LL find(LL x) {int z=x%maxh; for (int i=first[z];i;i=edge[i].next) if (edge[i].to==x) return edge[i].v; return -1;} 26 }h; 27 28 void pre(int &n) 29 { 30 lp=0; f[1]=sf[1]=1; 31 for (int i=2;i<=n;i++) 32 { 33 if (!notprime[i]) {prime[++lp]=i; f[i]=4; mi[i]=i; ci[i]=1;} 34 sf[i]=sf[i-1]+f[i]; s[i]=s[i-1]+!notprime[i]; 35 for (int j=1,tmp;j<=lp && 1ll*i*prime[j]<=n;j++) 36 { 37 notprime[tmp=i*prime[j]]=1; 38 if (i%prime[j]) {f[tmp]=f[i]*4; mi[tmp]=prime[j]; ci[tmp]=1;} 39 else {f[tmp]=f[i/mi[i]]*(3*ci[i]+4); mi[tmp]=mi[i]*prime[j]; ci[tmp]=ci[i]+1; break;} 40 } 41 } 42 lp--; n=prime[lp+1]-1; 43 } 44 45 void mg() 46 { 47 lw=0; h.clear(n); 48 for (LL i=1;i<=n;i=n/(n/i)+1) lw++,who[lw]=g[lw]=n/i,h.insert(who[lw],lw); 49 memset(i0,0,sizeof(i0)); 50 for (int i=1;i<=lp;i++) 51 for (int j=1;j<=lw && prime[i]*prime[i]<=who[j];j++) 52 { 53 int k=h.find(who[j]/prime[i]); 54 g[j]-=g[k]-(i-1-i0[k]); 55 i0[j]=i; 56 } 57 } 58 59 void mff() 60 { 61 for (int j=1;j<=lw;j++) ff[j]=1; 62 for (int i=lp;i;i--) 63 for (int j=1;j<=lw && 1ll*prime[i]*prime[i]<=who[j];j++) 64 { 65 if (prime[i+1]>who[j]) ff[j]=1; 66 else if (prime[i+1]*prime[i+1]>who[j]) ff[j]=(s[min((LL)m,who[j])]-s[prime[i+1]-1])*4+1; 67 LL tmp=prime[i],k2; 68 for (int c=1;tmp<=who[j];tmp*=prime[i],c++) 69 { 70 LL k=who[j]/tmp; 71 if (prime[i+1]>k) k2=1; 72 else if (prime[i+1]*prime[i+1]>k) k2=(s[min((LL)m,k)]-s[prime[i+1]-1])*4+1; 73 else k2=ff[h.find(k)]; 74 ff[j]+=k2*(3*c+1); 75 } 76 } 77 } 78 79 int main() 80 { 81 scanf("%d",&T); 82 pre(m); 83 while (T--) 84 { 85 scanf("%lld",&n); 86 if (n<=m) {printf("%lld ",sf[n]); continue;} 87 LL ans=0,last; mg(); mff(); 88 for (int i=1,id;i<=m;i=last+1) 89 { 90 LL tmp=n/i,kk; 91 if (prime[lp+1]>tmp) kk=1; 92 else id=h.find(tmp),kk=g[id]-(lp-i0[id]); 93 ans+=(sf[last=min((LL)m,n/tmp)]-sf[i-1])*(kk-1)*4; 94 } 95 printf("%lld ",ans+ff[1]); 96 } 97 return 0; 98 }
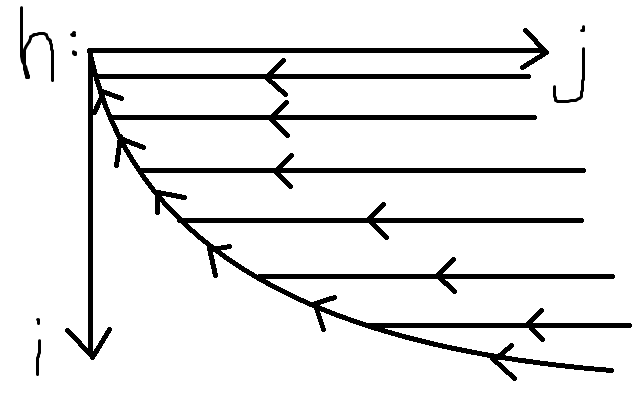
配俩图,表示$g$和$h$的递推顺序。