树链剖分
参考
*转载请注明出处,部分内容引自banananana大神的博客*
树链剖分
树刨的定义
树剖是通过轻重边剖分将树分割成多条链,然后利用数据结构来维护这些链(本质上是一种优化暴力)
定义
父亲结点:具有儿子结点的结点(儿子结点:具有父亲结点的结点)
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
轻儿子:父亲节点中除了重儿子以外的儿子;
- 一个父亲结点只会偏宠爱一个儿子结点(唯一个优先继承人)。
重边:父亲结点和重儿子连成的边;
(连续去选择重儿子连接)
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径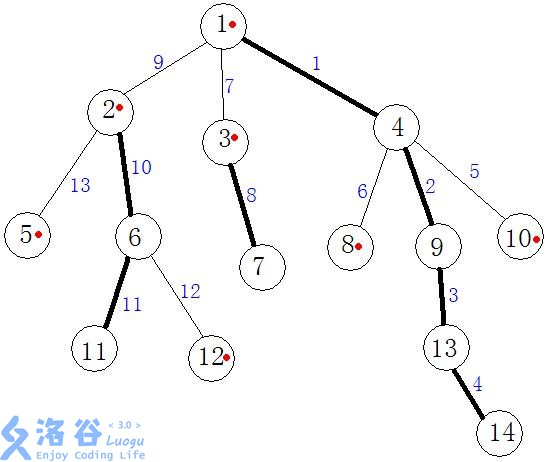
结点1有2,3,4三个儿子结点,其中以2为根节点的子树总共拥有5个结点,以3为根结点的子树一共拥有2个结点,以4为根节点的子树总共拥有6个结点。
因而作为父亲结点的1会优先选择结点4来作为自己的重儿子,而重儿子一旦选定,其他的儿子结点就是其轻儿子。
然后图中的粗黑线的关系代表的是父亲结点和重儿子结点之间的关系,即所谓的
重边,而其他相对细的边就为轻边
而我们可以取多条连续的重边,用它们来组成重链,比如1-4-9-13-14。
而我们可以取多条连续的轻边,用它们来组成轻链,比如1-2-5。
程序实现
由于我们要判断一个儿子结点是否为重儿子,因为我们就需要把每一个儿子结点所在的子树的包含的结点的个数给统计出来。
因而,我们需要开辟一个数组,名为size,用来统计子树的结点个数(其中size[u],代表的以u为根节点的子树的结点树),然后也不能白干活啊,因而我们需要对重儿子进行保留,开辟一个数组名为son(其中son[u]代表的是结点u的重儿子)。
- 关于重儿子的讨论
如果一个点的多个儿子所在子树大小相等且最大
那随便找一个当做它的重儿子就好了
叶节点没有重儿子,非叶节点有且只有一个重儿子
然后再进行标记(跑dfs)的时候为了不回到父亲结点,我们可以再定义一个数组f(其中f[x]表示的是x结点的父亲结点)
然后这里已经做完了预处理操作了。
void dfs1(int u,int fa,int depth)
{
f[u]=fa;//root结点的父亲结点可以令为-1或0
d[u]=depth;//随着递归的深度而改变
size[u]=1;//初始化本子树的结点数,然后再搜索的过程中给汇集起来
for(遍历u的边)
{
提取边上的另一个端点v
若是v是父亲结点就跳过
否则往深继续跑dfs;
size[u]+=size[v];//自下而上返还得到结点数
if(size[v]>size[son[u]])//筛选出真正的重儿子
son[u]=v;
}
}
dfs1(root,0或者-1,1);

dfs跑完大概是这样的,大家可以手动模拟一下
(逃命)
做个小的总结
| 数组名称 | 解释 |
|---|---|
| f | 表示当前结点的父亲结点,若其值为0或者-1,代表该点是root。 |
| d | 表示当前结点的深度,是父亲结点的深度加一,为了保证数组不越界,可使根节点的父亲结点为0。 |
| size | 表示以当前结点为根节点的子树的总结点树。 |
| son | 表示当前结点的重儿子,如果其值为0,表示当前结点为叶子结点,不具备有任何的儿子结点。 |
第一遍的dfs提前处理好每一个可行的结点的重儿子结点是哪一个,但仍还没有形成链,因而我们还需要对图再进行一次统计操作(再跑一遍dfs)
然后关于重链的探索,我们很清楚得知道得是当前结点连上它的重儿子结点可以形成一条重边,而这条重边就是重链的一个组成部分。而对于它的轻儿子来说,也不要灰心,它可能本身就是一条重链的顶端结点(为什么说是可能呢?因为这个结点可能是一个叶子结点,它是无法再继续形成一条重链的,也就是图中的结点5。
关于第二遍dfs我们需要准备的数组有top,(其中top[x]代表结点x的所在链的链头结点),也就是说如果有top[x]==top[y],则说明结点x和结点y是在同一条重链上。
son[x]==0代表结点x是叶子结点。
void dfs2(int u,int t)//当前结点,当前结点所处在的重链的顶端
{
top[u]=t;
//id[u]=++cnt;//dfs序,对点的重新标号,这步是为了后面线段树的操作
//rk[cnt]=u;//从新标号重新映射回去到实际结点
if(!son[u])
reutrn ;
dfs2(son[u],t);//再续良缘
for(扫描u的边)
{
提取边上的另一个端点v
如果v不是u的重儿子且不是u的父亲结点的话
dfs2(v,v); //以轻儿子为新的一条可能的重链的顶端和新的当前结点dfs下去
}
}
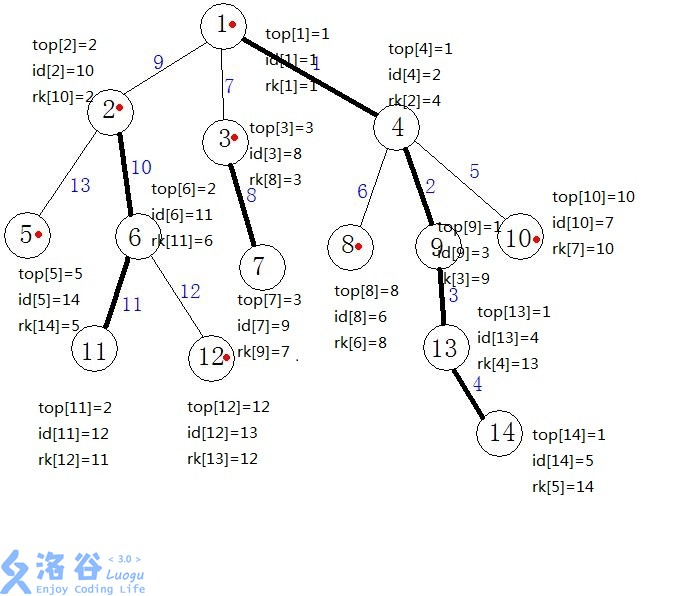
第二遍dfs
| 数组名称 | 解释 |
|---|---|
| top | 当前结点所在的重链的链头结点 |
| id | 当前在dfs2实际访问得到的顺序,由于dfs2的设计,所以一条重链/子树的所有点的id是连续的(这点这是线段树的可以用来维护重链的一个很重要的前提条件) |
| rk | 通过dfs2序重新映射回起初的结点编号 |
两遍dfs跑完的结果。
dfs跑完大概是这样的,大家可以手动模拟一下
int sum(int x,int y)//代表的是x和y两个结点
{
int ans=0,fx=top[x],fy=top[u];
while(fx!=fy)//如果x和y不在同一条重链
{
if(d[fx]>=d[fy])//x的重链链头结点比y的重链链头结点的深度还低。
{
ans+=query(u,id[fx],id[x]);
x=f[fx],fx=top[x];//将x设置其重链链头结点的父亲结点,fy为新结点所在重链的链头结点。
}
else
{
ans+=query(u,id[fy],id[y]);
y=f[fy],fy=top[y];
}
}
//while语句处理完后,x,y两个结点将同时处于一条重链上,也就意味这我们要单独去处理这两点之间的贡献
if(id[x]<=id[y])//由于线段树区间的特性,要找到id比较小的,让它排到前面去
ans+=query(u,id[x],id[y]);
else
ans+=query(u,id[y],id[x]);
return ans;
}
题目
AcWing_2568. 树链剖分
可先跳转到其他
操作一
对于操作一,修改路径上节点权值,将节点 u和节点 v 之间路径上的所有节点(包括这两个节点)的权值增加 k。
由于dfs序的特性,我们可以将u,v中一条重链给扔到线段树的update函数更新掉,同时不断更新u和v,并且重复之前的操作,直到u和v在同一条重链上。
操作二
对于操作二,由于dfs序的特性,我们只需要将结点位置和结点位置加上其子树结点数的值扔到线段树的update函数里面就行。
操作三和操作四
这两种操作本质是和前两者对应相等的。
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
x=x*10+ch-'0',ch=getchar();
return x*f;
}
const int N = 3e5+10 , M = 6e5+10;
int h[N],ne[M],e[M],idx;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
struct node{
int l,r;
ll sum,lz;
}tr[N<<2];
int n,m;
int d[N],f[N],sz[N],son[N];
void dfs1(int u,int fa,int dep)
{
d[u]=dep,f[u]=fa,sz[u]=1;
for(int i=h[u];~i;i=ne[i])
{
int v = e[i];
if(v==fa) continue;
dfs1(v,u,dep+1);
sz[u]+=sz[v];
if(sz[v]>sz[ son[u] ])
son[u] = v;
}
}
int top[N],id[N],ival[N],val[N],cnt;
void dfs2(int u,int t)
{
id[u]=++cnt,ival[cnt]=val[u],top[u]=t;
if(!son[u]) return ;//叶子结点果断跳出
dfs2(son[u],t);
for(int i = h[u];~i;i=ne[i])
{
int v = e[i];
if(v==f[u]||v==son[u]) continue;
dfs2(v,v);
}
}
/****线段树****/
void pushup(int u)
{
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void pushdown(int u)
{
tr[u<<1].lz+=tr[u].lz;
tr[u<<1].sum+=tr[u].lz*(tr[u<<1].r-tr[u<<1].l+1);
tr[u<<1|1].lz+=tr[u].lz;
tr[u<<1|1].sum+=tr[u].lz*(tr[u<<1|1].r-tr[u<<1|1].l+1);
tr[u].lz=0;
}
void build(int u,int l,int r)
{
tr[u]={l,r,0,0};
if(l==r)
{
tr[u]={l,r,ival[l],0};
return ;
}
int mid = l+r>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
pushup(u);
}
ll query(int u,int l,int r)
{
if(l<=tr[u].l&&tr[u].r<=r)
return tr[u].sum;
pushdown(u);
ll res=0,mid = tr[u].l + tr[u].r >>1;
if(l<=mid) res+=query(u<<1,l,r);
if(mid+1<=r) res+=query(u<<1|1,l,r);
return res;
}
void modi(int u,int l,int r,int k)
{
if(l<=tr[u].l&&tr[u].r<=r)
{
tr[u].lz+=k;
tr[u].sum+=k*(tr[u].r-tr[u].l+1);
return ;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1 ;
if(l<=mid) modi(u<<1,l,r,k);
if(mid+1<=r) modi(u<<1|1,l,r,k);
pushup(u);
}
/****四种操作****/
void modi_tree(int u,int k)
{
modi(1,id[u],id[u]+sz[u]-1,k);
}
void modi_route(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(d[ top[x] ]<d[ top[y] ])
swap(x,y);
modi(1,id[ top[x] ],id[x],k);
x = f[ top[x] ];
}
if( d[x]<d[y]) swap(x,y);
modi(1,id[y],id[x],k);
}
ll query_tree(int u)
{
return query(1,id[u],id[u]+sz[u]-1);
}
ll query_route(int x,int y)
{
ll res = 0;
while(top[x]!=top[y])
{
if(d[ top[x] ]<d[ top[y] ])
swap(x,y);
res += query(1,id[ top[x] ],id[x]);
x = f[ top[x] ];
}
if(d[x]<d[y]) swap(x,y);
res += query(1,id[y],id[x]);
return res;
}
int main()
{
int n = read();
memset(h,-1,sizeof(h));
for(int i=1;i<=n;i++)
val[i] = read();
for(int i=1;i<=n-1;i++)
{
int a = read(),b = read();
add(a,b),add(b,a);
}
dfs1(1,-1,1);
dfs2(1,1);
build(1,1,n);
int opts = read();
for(int i=1;i<=opts;i++)
{
int opt = read(),u,v,k;
if(opt==1)
{
u = read(),v = read(),k = read();
modi_route(u,v,k);
}
else if(opt==2)
{
u = read(),k = read();
modi_tree(u,k);
}
else if(opt==3)
{
u = read(),v = read();
printf("%lld
",query_route(u,v));
}
else if(opt==4)
{
u = read();
printf("%lld
",query_tree(u));
}
}
return 0;
}
其他
线段树懒标记(以区间和为例)
线段树懒标记下放
- 懒标记在当前结点是已经实现了效果的
void pushdown(int u)
{
if(tr[u].lazy)
{
/***左下传***/
tr[u<<1].sum+=tr[u].lazy*(tr[u<<1].r-tr[u<<1].l+1);
tr[u<<1].lazy+=tr[u].lazy;
/***右下传***/
tr[u<<1|1].sum+=tr[u].lazy*(tr[u<<1|1].r-tr[u<<1|1].l+1);
tr[u<<1|1].lazy+=tr[u].lazy;
/***懒标记归零***/
tr[u].lazy=0;
}
}
-
懒标记下放的时机的选择
为了在查询过程中信息的准确,如果没有下放使得信息更新不及时从而导致没有得到准确的信息的话,那么就是没有在应该下放懒标记的时机下放懒标记了。
比如想要查询区间和/更新,如果需要查询/更新下一层的信息,就需要释放本层的懒标记。
-
pushdown在更新子节点前,是为了得到子节点的正确信息,pushup在更新子节点后,是为了更新当前结点的信息,pushup是在更新操作中,而不在查询操作中,因为在查询操作中子节点不影响到父节点。
void pushup(int u)//收集儿子结点的信息 { tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum; }