斜率优化DP讲解

　　对于斜率优化的DP转移方程，一般以w[i]=max(w[j]+(sum[i]-sum[j])*v)的1D1D形式为主，直观看来就是前j个为若干个阶段，第j+1到第i个为一个阶段，每个阶段有自己的代价或价值。

　　我们从一道题来入手，bzoj 1911 http://61.187.179.132/JudgeOnline/problem.php?id=1911 这是一道典型的斜率优化题，作为练手的入门题再适合不过。

　　这道题的大概意思为将1-n个数划分为若干区间，每个区间有一个价值=a*Σ(a[i])^2+b*Σ(a[i])+c，最后使代价和最大。

　　设前缀和为sum，那么很容易写出转移方程w[i]:=max(w[j]+a*(sum[i]-sum[j])*(sum[i]-sum[j])+c)，但是这样的时间复杂度为n^2，显然不能通过全部测试数据。那么我们考虑斜率优化。

　　假设当前需要转移到第i个数，对于i的最优解为j，那么我们需要证明对于任意k>j都有j比k更优。（k<j时下文会提到）

　　那么我们可以得到式子w[j]+a*(sum[i]-sum[j])*(sum[i]-sum[j])+c>w[k]+a*(sum[i]-sum[k])*(sum[i]-sum[k])+c

　　经整理我们可以得到(w[j]+a*sum[j]*sum[j]-b*sum[j])-(w[j]+a*sum[j]*sum[j]-b*sum[j])>2*a*sum[i]*(sum[j]-sum[k])

　　因为j<k且数列的每一项>0所以sum[j]-sum[k]<0，所以我们将sum[j]-sum[k]除到式子的左面，那么可以得到

　　

　　((w[j]+a*sum[j]*sum[j]-b*sum[j])-(w[j]+a*sum[j]*sum[j]-b*sum[j]))/(sum[j]-sum[k])<2*a*sum[i]

　　显然对于式子的右面，只与当前的i有关，与j与k无关，那么式子的左面，我们可以将他写成类似于斜率的式子。

　　设g(i)=w[i]+a*sum[i]*sum[i]-b*sum[i]，那么式子可以写成((g(j)-g(k))/(sum[j]-sum[k]))<2*a*sum[i]，也就是说当g(j)与g(k)满足当前关系时，j比k更优，那么我们将g(i)当成纵坐标，sum[i]当成横坐标，就可以将转移表示为坐标系中的斜率

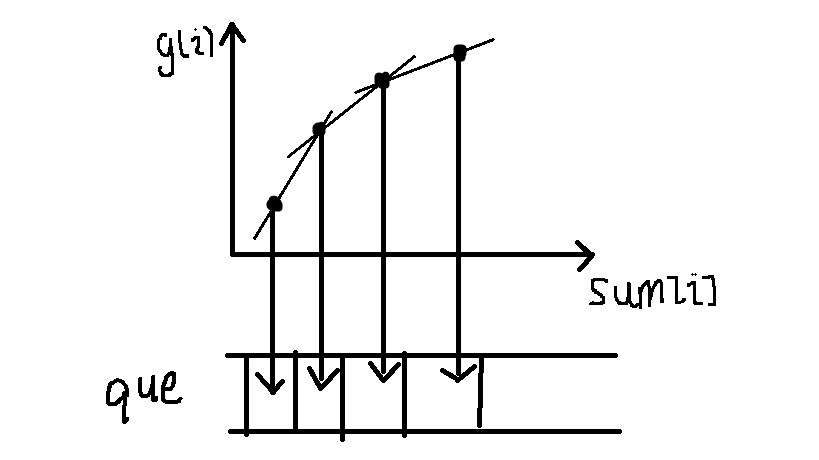
　　因为sum为递增的，我们可以维护这样的一个下凸壳，这个凸壳满足一些性质：

　　首先对于队首向后考虑，每两个相邻的元素的斜率为递增的，再考虑斜率的表达式

　　((w[j]+a*sum[j]*sum[j]-b*sum[j])-(w[j]+a*sum[j]*sum[j]-b*sum[j]))/(sum[j]-sum[k])，这也就是我们刚才证明的式子，这样的式子如果对于<2*a*sum[i]成立，即表示对于当前i状态，j优于k，那么假设队的第一二元素满足该式，之后斜率递减，则之后任意两个相邻的元素都满足。这代表队首的状态优于队的第二个，同时优于之后每一个元素，即j为当前转移的i的最优解。

　　那么假设当前队首与第二元素的斜率大于2*a*sum[i]，那么代表队中第二元素状态优于队首，那么对于之后的任意2*a*sum[j]，sum[j]为递增，a<0，所以这里为递减的，即2*a*sum[i]>2*a*sum[j]，又因为k(队首，队第二)>2*a*sum[i]>2*a*sum[j]，所以对于之后的所有状态，队中第二元素都优于第一元素，所以队首没有价值了，出队即可。

　　进队时，因为需要满足第一性质中斜率不断减小的性质，所以保证k(队末-1，队末)< k(队末-1，当前元素)就行了。具体的证明可以去看这里的报告http://akheyun.blog.163.com/blog/static/138249276201071372635257/

/**************************************************************
    Problem: 1911
    User: BLADEVIL
    Language: Pascal
    Result: Accepted
    Time:2552 ms
    Memory:23664 kb
****************************************************************/
 
//By BLADEVIL
var
    w, g                    :array[0..1000010] of int64;
    sum                     :array[0..1000010] of longint;
    q                       :array[0..1000010] of longint;
    a,b,c                   :int64;
    n                       :longint;
      
procedure init;
var
    i                       :longint;
begin
    read(n); read(a,b,c);
    for i:=1 to n do
    begin
        read(sum[i]);
        sum[i]:=sum[i]+sum[i-1];
    end;
end;
  
function k(x,y:longint):extended; 
begin
    k:=(g[y]-g[x])/(sum[y]-sum[x]);
end; 
  
procedure main;
var
    i                       :longint;
    h, t                    :longint;
    cur                     :extended;
begin
    w[0]:=0;
    h:=1; t:=1;
    q[1]:=0;
    for i:=1 to n do
    begin
        cur:=2*a*sum[i];
        while (t-h>0)and (k(q[h],q[h+1])>cur) do inc(h);
        w[i]:=w[q[h]]+a*int64(sum[i]-sum[q[h]])*int64(sum[i]-sum[q[h]])+b*int64(sum[i]-sum[q[h]])+c;
        g[i]:=w[i]+a*int64(sum[i])*int64(sum[i])-b*int64(sum[i]);
        while (t-h+1>=2)and(k(q[t],i)>k(q[t-1],q[t])) do dec(t);
        inc(t);
        q[t]:=i;
    end;
    writeln(w[n]);
end;
  
begin
    init;
    main;
end.