对数函数

写在前面：

　　高考复习笔记

定义
历史
性质

定义

　　对数函数是以幂（真数）为自变量，指数为因变量，底数为常量的函数。

历史

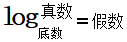
　　“log”是拉丁文logarithm的缩写。

　　16世纪末至17世纪初的时候，当时在自然科学领域（特别是天文学）的发展上经常遇到大量精密而又庞大的天文数值计算，于是数学家们为了寻求化简的计算方法而发明了对数。德国的M.Stifel在1544年所著的《整数算术》中，写出了两个数列，左边是等比数列（叫原数），右边是一个等差数列。欲求左边任两数的积（商），只要先求出其代表（指数）的和（差），然后再把这个和（差）对向左边的一个原数，则此原数即为所求之积（商），可惜Stifel并未作进一步探索，没有引入对数的概念。

　　在John Napier所处的年代，哥白尼的“太阳中心说”刚刚开始流行，这导致天文学成为当时的热门学科。可是由于当时常量数学的局限性，天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”，因此浪费了若干年甚至毕生的宝贵时间。

　　Napier也是当时的一位天文爱好者，他所制造的「Napier算筹」，化简了乘除法运算，其原理就是用加减来代替乘除法。他发明对数的动机是为寻求球面三角计算的简便方法，他依据一种非常独等的与质点运动有关的设想构造出所谓对数方法，其核心思想表现为算术数列与几何数列之间的联系。在他的1619年发表《奇妙的对数表的描述》中阐明了对数原理，后人称为Napier对数，记为Nap．㏒x，它与自然对数的关系为：Nap．㏒x=10㏑(107/x)。

　　由此可知，Napier对数既不是自然对数，也不是常用对数，与现今的对数有一定的距离。瑞士的Burgi也独立地发现了对数，可能比Napier较早，但发表较迟（1620）。英国的Briggs在1624年创造了常用对数。1619年，伦敦John Speidell所著的《新对数表》使对数与自然对数更接近（以e=2.71828...为底）。

　　对数的发明为当时社会的发展起了重要的影响，简化了行星轨道运算问题。

性质

定义域

　　真数>0

值域

　　实数集R，显然对数函数无界。

单调性

　　底数>1时，在定义域上为单调增函数；

　　0<底数<1时，在定义域上为单调减函数。

奇偶性

　　非奇非偶函数。

周期性

　　无。

对称性

　　无。

最值

　　无。

零点

　　x=1。

基本性质

　　①a^log_a(b) = b
　　②log_a(a^b) = b
　　③log_a(M*N) = log_a(M)+log_a(N)
　　④log_a(M/N) = log_a(M)-log_a(N)
　　⑤log_a(Mⁿ) = n*log_a(M)
　　⑥log_aⁿ(M) = (1/n)*log_a(M)

其他性质

　　对数函数的函数图像恒过定点(1,0)。

　　“底大图低”：

　　　　两个对数函数的真数相同时，无论底数在(0,1)还是(1,+∞)，底数大的那个假数距离x轴近。

　　“同正异负”：

　　　　真数和底数都在(0,1)或都在(1,+∞)时，假数为正。

　　　　真数在(0,1)而底数在(1,+∞)，或者真数在(1,+∞)而底数在(0,1)时，假数为负。

反函数

　　　　指数函数。

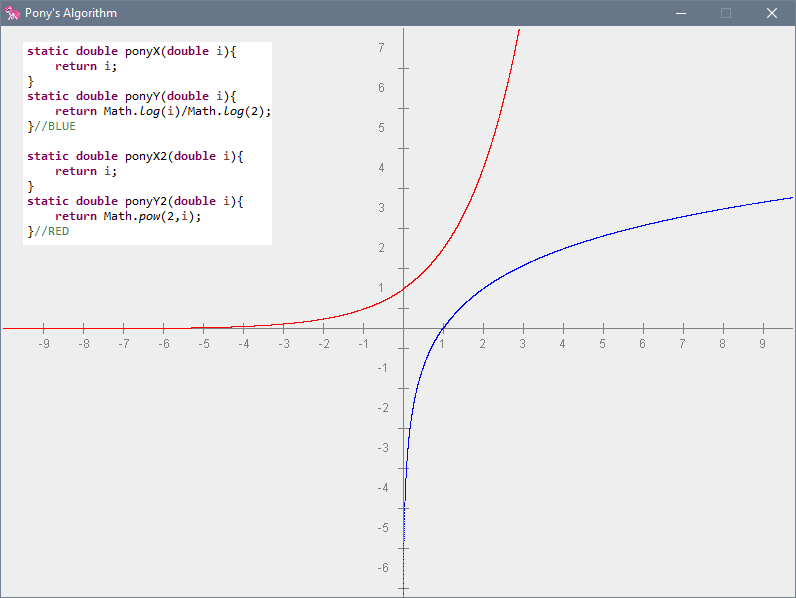
图示中函数：2^x和log₂(x)