写在前面:
高考复习笔记
有原创内容(大概吧呃呃呃)

http://rhads.deviantart.com/art/KIRIBAN-77777-362416675
|
目录 |
定义
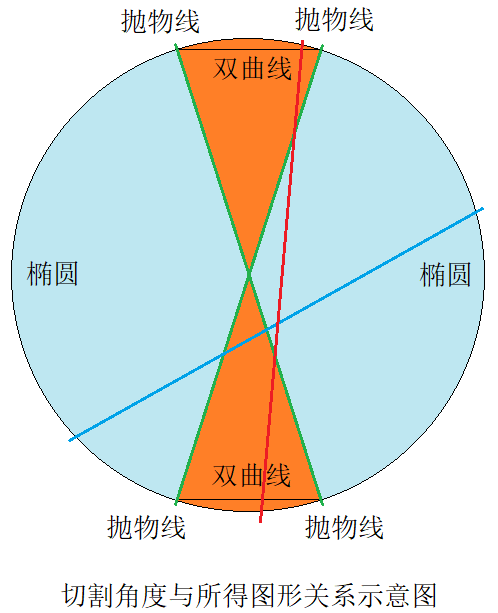
圆锥曲线是由一平面截二次锥面得到的曲线,包括椭圆、抛物线、双曲线(高中认为圆不是椭圆)。

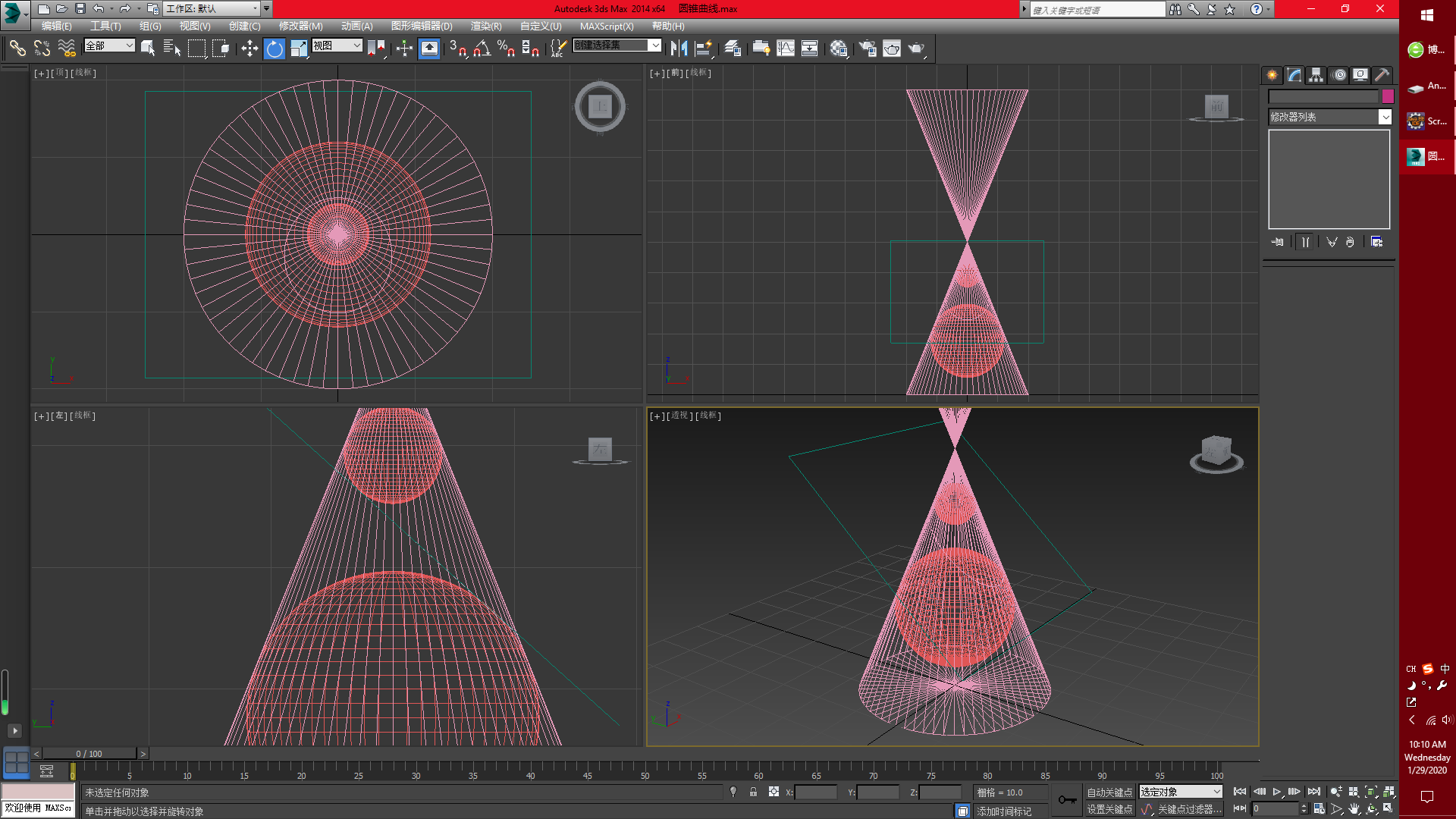
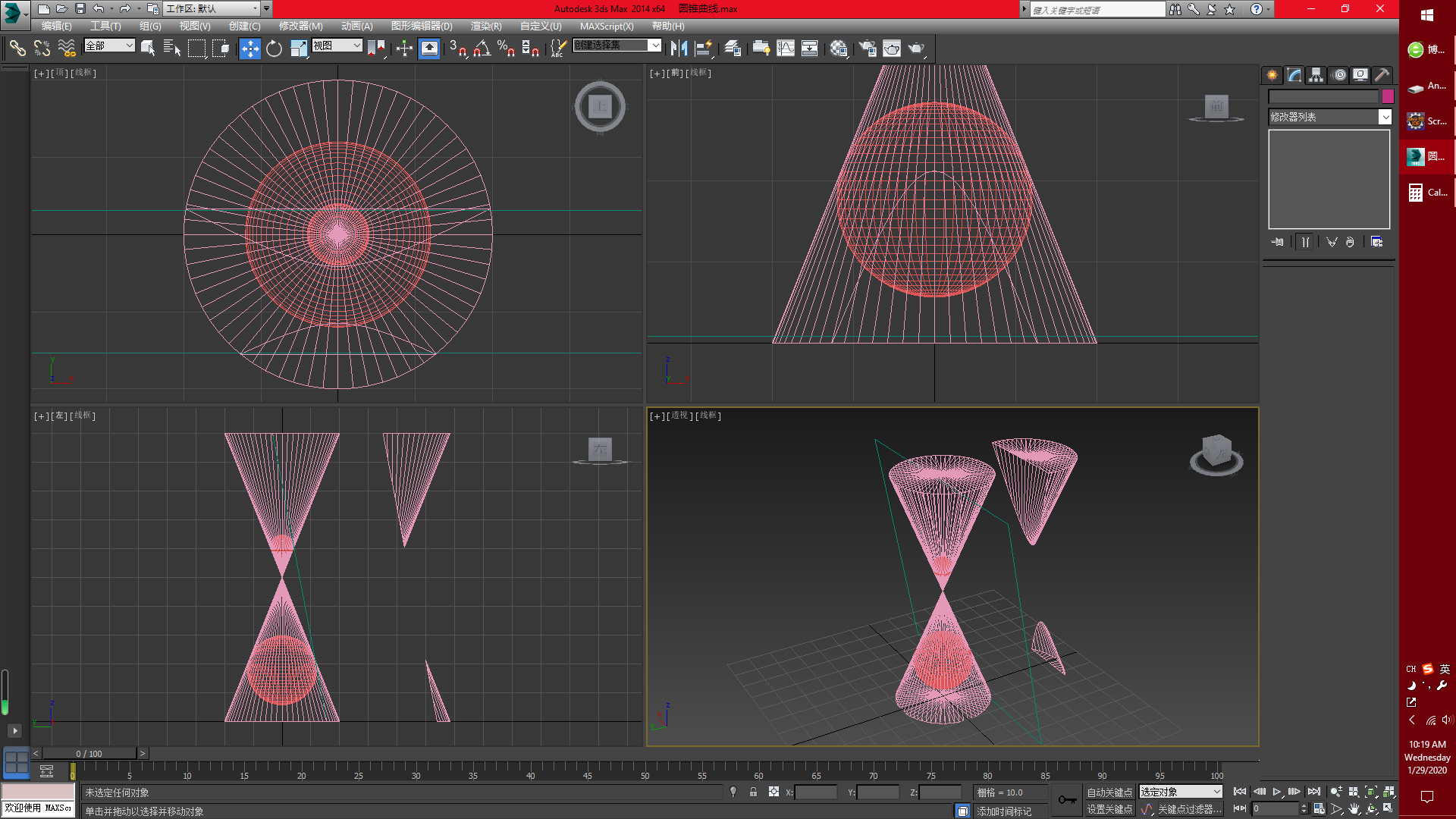
抛物线不是双曲线的一支(下图中仍然为双曲线而不是抛物线)

椭圆第一定义:平面内,到两定点F1、F2的距离的和等于常数2a的点的集合。(2a>|F1F2|)
椭圆第二定义:平面内,到定点F距离与到定直线l间距离之比为常数e的点的集合。(定点F不在定直线上,e为离心率,0<e<1,左准线配左焦点,右准线配右焦点)
椭圆第三定义:平面内,到两定点的斜率乘积等于常数 e2- 1的点的集合(再补上斜率不存在的直线对应的点)。(然后可以规定两定点连线中点为原点)(e为离心率,0<e<1)
表示方法:
①标准方程
焦点在x轴上: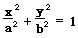
焦点在y轴上:
规律:a在谁下面,焦点就在谁上
②参数方程
焦点在x轴上: 或
或 
焦点在y轴上: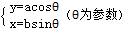 或
或 
规律:a和谁在一起,焦点就在谁上

原理:
若取内切圆的y坐标为椭圆y坐标,取外接圆的x坐标为椭圆x坐标,焦点就在x轴上
若取内切圆的x坐标为椭圆x坐标,取外接圆的y坐标为椭圆y坐标,焦点就在y轴上

③极坐标:略
图例:

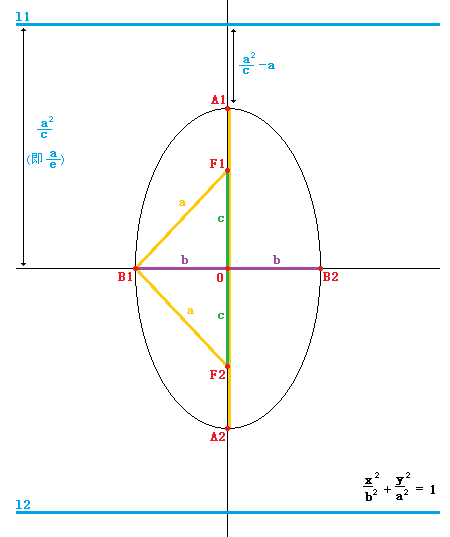
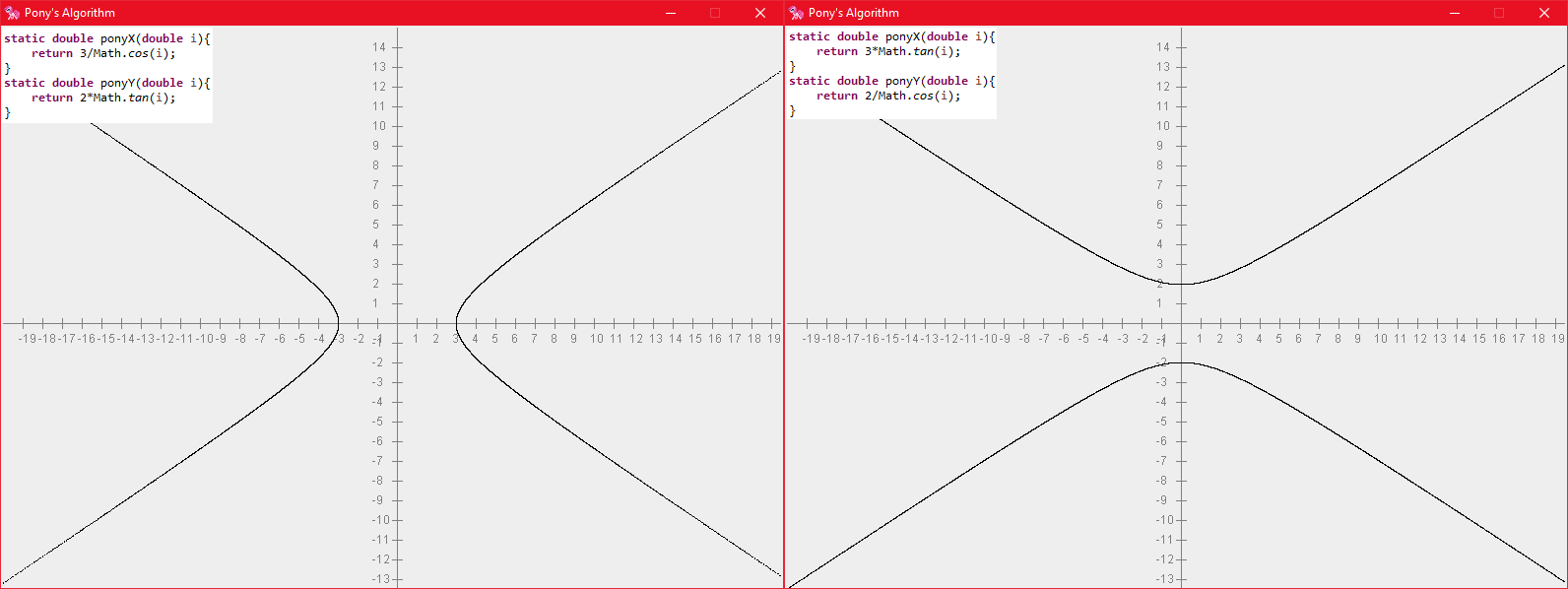
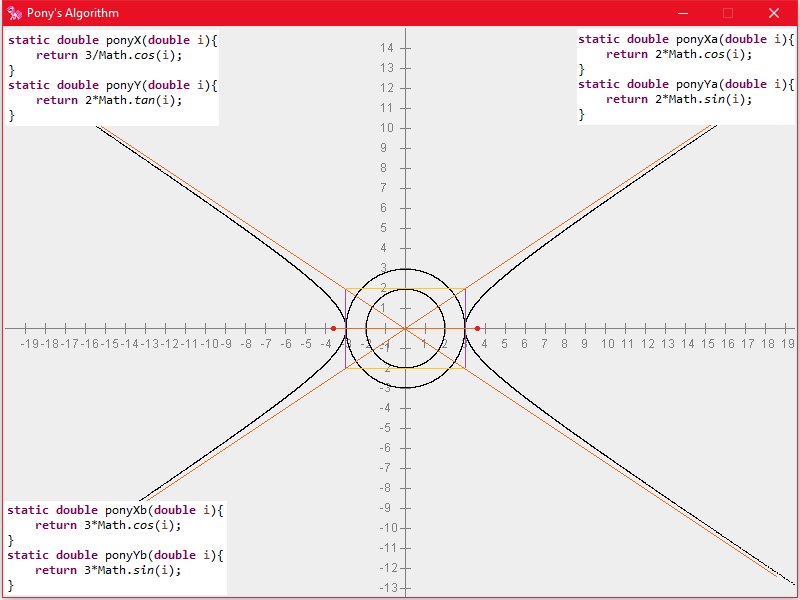
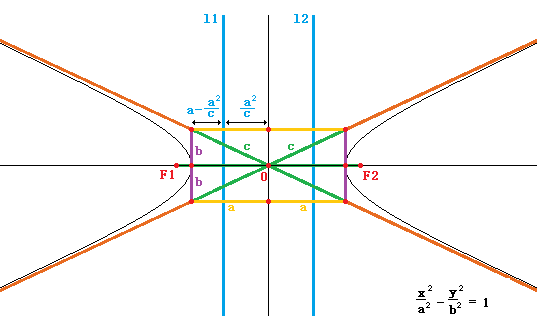
双曲线第一定义:平面内,到两定点F1、F2的距离之差的绝对值为常数2a的点的集合。
双曲线第二定义:平面内,到定点F及直线l的距离之比为常数e的点的集合。(定点F不在定直线上,e为离心率,1<e,左准线配左焦点,右准线配右焦点)
双曲线第三定义:平面内,到两定点的斜率乘积等于常数 e2- 1的点的集合(再补上斜率不存在的直线对应的点)。(然后可以规定两定点连线中点为原点)(e为离心率,1<e)(因为顺序问题,过两定点的直线不可能是之后作出来的双曲线的渐近线)
表示方法:
①标准方程
焦点在x轴上: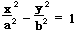
焦点在y轴上:
规律:谁是正的,焦点和实轴就在谁上
②参数方程
焦点在x轴上: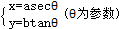
焦点在y轴上:
规律:sec和谁在一起,焦点和实轴就在谁上
原理:
③极坐标:略
图例:

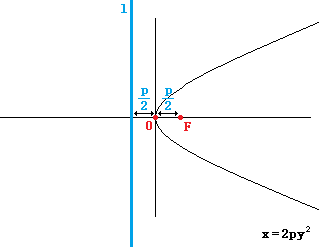
抛物线定义:到定点F及直线l的距离之比为1的点的集合。(定点F不在定直线上,e为离心率,e=1)
表示方法:
①标准方程
焦点在x轴正半轴:x = 2py2
焦点在x轴负半轴:x = -2py2
焦点在y轴正半轴:y = 2px2
焦点在y轴负半轴:y = -2px2
规律:带“-”就在负半轴,谁是一次的焦点在谁上
②参数方程:略
③极坐标:略
图例:
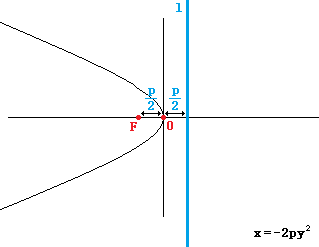

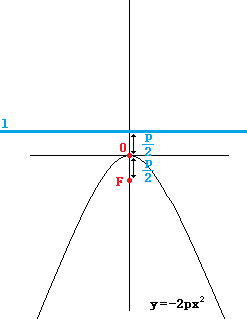
历史
对于圆锥曲线的最早发现,众说纷纭。
有人说,古希腊数学家在求解“立方倍积”问题时,发现了圆锥曲线。
又有人说,古希腊数学家在研究平面与圆锥面相截时发现了与“立方倍积”问题中一致的结果。
还有认为,古代天文学家在制作日晷时发现了圆锥曲线(然而日晷在古代已失传)。
早期对圆锥曲线进行系统研究成就最突出的可以说是古希腊数学家Apollonius。他与Euclid是同时代人,其巨著《圆锥曲线》与Euclid的《几何原本》同被誉为古代希腊几何的登峰造极之作。
在《圆锥曲线》中,Apollonius总结了前人的工作,尤其是Euclid的工作,并对前人的成果进行去粗存精、归纳提炼并使之系统化的工作,在此基础上,又提出许多自己的创见。全书8篇,共487个命题,将圆锥曲线的性质网罗殆尽,以致后代学者几乎没有插足的余地达千余年。
常见性质
 1.椭圆第一定义
1.椭圆第一定义
 2.椭圆第二定义
2.椭圆第二定义
 3.椭圆第三定义
3.椭圆第三定义
 4.焦半径长公式:
4.焦半径长公式:
焦半径:连结椭圆上一点与对应焦点的线段的长度,叫做椭圆焦半径
①无论P(x0,y0)在椭圆上哪里,焦点在x轴上:r =a+ex0(左焦点) r =a-ex0(右焦点)
②无论P(x0,y0)在椭圆上哪里,焦点在y轴上:r =a-ex0(上焦点) r =a+ex0(下焦点)
 5.通经长公式:
5.通经长公式:
通径:过圆锥曲线的焦点且与过焦点的轴垂直的弦称为通径
 (无论焦点在哪个轴)
(无论焦点在哪个轴)
 6.椭圆中的圆:
6.椭圆中的圆:
①以焦点弦为直径的圆与其对应的准线相离
②以焦半径为直径的圆与以长轴为直径的圆内切
 7.弦AB所在直线的斜率kAB与其中点M和原点O连线的斜率kOM乘积:
7.弦AB所在直线的斜率kAB与其中点M和原点O连线的斜率kOM乘积:
①焦点在x轴 
②焦点在y轴 
 8.过椭圆上一点P(x0,y0)的切线方程:
8.过椭圆上一点P(x0,y0)的切线方程:
①焦点在x轴 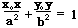
②焦点在y轴 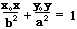
 9.过椭圆外一点P(x0,y0)的两条切线,两切点所在直线方程:
9.过椭圆外一点P(x0,y0)的两条切线,两切点所在直线方程:
①焦点在x轴 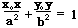
②焦点在y轴 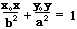
 10.弦长公式:
10.弦长公式:
已知椭圆上不重合两点A(x1,y1),B(x2,y2)

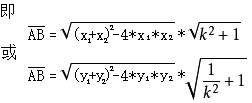
 1.双曲线第一定义
1.双曲线第一定义
 2.双曲线第二定义
2.双曲线第二定义
 3.双曲线第三定义
3.双曲线第三定义
 4.渐近线斜率:
4.渐近线斜率:
①焦点在x轴 k1= k2=
k2=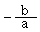
②焦点在y轴 k1= k2=
k2=
 5.共轭双曲线:
5.共轭双曲线:
如果一双曲线的实轴及虚轴分别为另一双曲线的虚轴及实轴,则此二双曲线互为共轭双曲线
①共轭双曲线的四个焦点共圆
②共轭双曲线离心率的平方和等于离心率的平方积
 6.等轴双曲线(直角双曲线):
6.等轴双曲线(直角双曲线):
实轴和虚轴相等的双曲线叫作等轴双曲线(直角双曲线)
①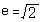
②半实轴长与半虚轴长相等
③两条渐近线斜率为k1=1,k2=-1,两条渐近线相互垂直
 7.焦半径长公式:
7.焦半径长公式:
焦半径:连结双曲线上一点与对应焦点的线段的长度,叫做双曲线焦半径
①P(x0,y0)在双曲线左支,焦点在x轴上:r = -a-ex0(左焦点) r = a-ex0(右焦点)
②P(x0,y0)在双曲线右支,焦点在x轴上:r = a-ex0(左焦点) r = -a-ex0(右焦点)
③P(x0,y0)在双曲线上支,焦点在y轴上:r = -a-ex0(上焦点) r = a-ex0(下焦点)
④P(x0,y0)在双曲线下支,焦点在y轴上:r = a-ex0(上焦点) r = -a-ex0(下焦点)
 8.通经长公式:
8.通经长公式:
通径:过圆锥曲线的焦点且与过焦点的轴垂直的弦称为通径
 (无论焦点在哪个轴)
(无论焦点在哪个轴)
 9.双曲线中的圆:
9.双曲线中的圆:
①以焦点弦为直径的圆与对应准线相交
②以焦半径为直径的圆与实轴为直径的圆外切
 10.弦长公式:
10.弦长公式:
已知双曲线上不重合两点A(x1,y1),B(x2,y2)


 11.弦AB所在直线的斜率kAB与其中点M和原点O连线的斜率kOM乘积:
11.弦AB所在直线的斜率kAB与其中点M和原点O连线的斜率kOM乘积:
①焦点在x轴 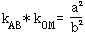
②焦点在y轴 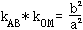
 12.过双曲线上一点P(x0,y0)的切线方程:
12.过双曲线上一点P(x0,y0)的切线方程:
①焦点在x轴 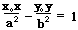
②焦点在y轴 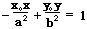
 13.过双曲线外一点P(x0,y0)的两条切线,两切点所在直线方程:
13.过双曲线外一点P(x0,y0)的两条切线,两切点所在直线方程:
①焦点在x轴 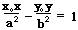
②焦点在y轴 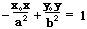
 1.抛物线定义
1.抛物线定义
 2.焦半径公式:
2.焦半径公式:
焦半径:连结抛物线上一点与对应焦点的线段的长度,叫做抛物线焦半径
①焦点在x轴上:P(x0,y0),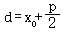
②焦点在y轴上:P(x0,y0),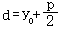
 3.通经长公式:
3.通经长公式:
通径:过圆锥曲线的焦点且与过焦点的轴垂直的弦称为通径
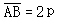 (无论焦点在哪个轴)
(无论焦点在哪个轴)
 4.弦长公式 :
4.弦长公式 :
已知抛物线上不重合两点A(x1,y1),B(x2,y2)

