随机变量可以粗略分为离散型随机变量和连续型随机变量两种。下面介绍这两种随机变量的典型分布。
离散型随机变量
1. 两点分布
随机变量X的取值有且只有0和1,其概率取值如下所示:
P(x=1)=p
P(X=0)=1-p
其中p∈(0,1)
两点分布是伯努利分布的一种特殊情况,即B(1,p)
2. 二项分布与超几何分布
二项分布与超几何分布的区别可以理解为二项分布是有放回的抽样,而超几何分布是无放回的抽样。形式化定义如下:
二项分布:
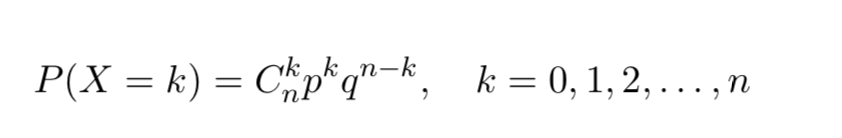
X服从二项分布记为,X~B(n,p)
超几何分布:
设有 N 个同类产品,其中 M 个次品。从中任取 n 个(假定n ≤ N − M)。则这 n 个中的次品数 X 是离散型随机变量 ,X服从超几何分布,概率分布如下所示:

3. 泊松分布
若随机变量X的分布为
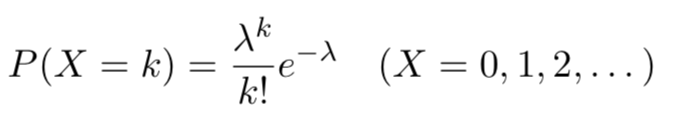
则X服从泊松分布,记为X~Possion(λ)
若二项分布的p很小,n很大,则可以用泊松分布近似计算二项分布。
连续型随机变量
对于随机变量 X,如果存在非负可积函数 p(x)(−∞ < x < ∞),使对任意 a, b(a < b) 都有
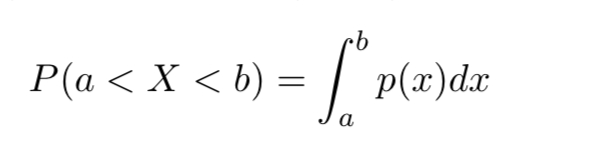
则称 X 为连续型随机变量,称 p(x) 为 X 的概率密度函数。
连续型随机变量不关心在某一点的概率,只关心在某一个区间的概率分布。
1. 均匀分布
若随机变量X服从均匀分布,即X~U[a,b],则X的概率密度函数如下所示:

2.指数分布
若随机变量X服从指数分布,即X~E(λ),则X的概率密度函数如下所示:
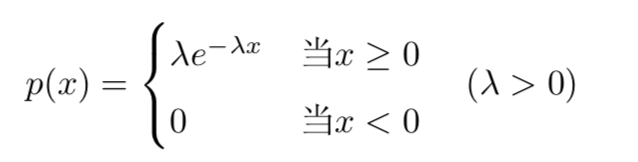
3.正态分布
若随机变量X服从正态分布,即X~N(μ,σ2 ),则X的概率密度函数如下所示:
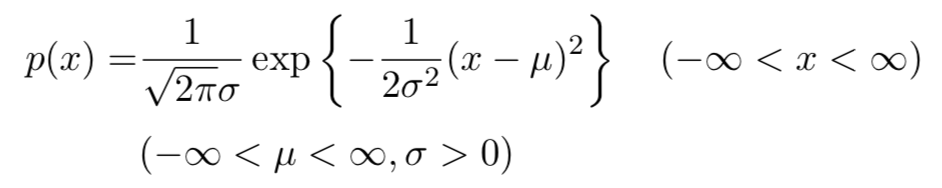
其中μ 决定曲线中心位置,σ 越大,曲线越平缓,σ 越小,曲线越陡峭。
当μ =0,σ2=1时,随机变量服从标准正态分布,此时概率密度函数是一个关于y轴对称的钟型曲线,一般情况下,一般正态分布都要标准化为N(0,1),标准化的方法为Y=(X-μ)/σ。
对于标准正态分布,概率密度函数和分布函数有特殊符号φ(t)、Φ(x)表示,即

则P(a < X < b) =Φ(b)−Φ(a) ,一般正态分布在某个区间的概率可以标准化后采用Φ表示其概率。
根据标准正态分布的对称性,可以得到如下公式
Φ(−x) = 1 − Φ(x), x ∈ (−∞,∞)