REFERENCE:
https://www.jianshu.com/p/ad528c40a08f
https://www.zhihu.com/question/54504471
图有两个基本的特性: 一是每个节点都有自己的特征信息。比如针对上图,我们建立一个风控规则,要看这个用户的注册地址、IP地址、交易的收货地址是否一样,如果这些特征信息不匹配,那么系统就会判定这个用户就存在一定的欺诈风险。这是对图节点特征信息的应用。 二是图谱中的每个节点还具有结构信息。如果某段时间某个IP节点连接的交易节点非常多,也就是说从某个IP节点延伸出来的边非常多,那么风控系统会判定这个IP地址存在风险。这是对图节点结构信息的应用。 总的来说,在图数据里面,我们要同时考虑到节点的特征信息以及结构信息,如果靠手工规则来提取,必将失去很多隐蔽和复杂的模式,那么有没有一种方法能自动化地同时学到图的特征信息与结构信息呢?——图卷积神经网络
Notes:
离散卷积的本质是加权求和
CNN中的卷积本质上就是利用一个共享参数的过滤器(kernel),通过计算中心像素点以及相邻像素点的加权和来构成feature map实现空间特征的提取,当然加权系数就是卷积核的权重系数。 那么卷积核的系数如何确定的呢?是随机化初值,然后根据误差函数通过反向传播梯度下降进行迭代优化。这是一个关键点,卷积核的参数通过优化求出才能实现特征提取的作用,GCN的理论很大一部分工作就是为了引入可以优化的卷积参数。
CNN在Computer Vision里效果为什么好呢?原因:可以很有效地提取空间特征。
但是有一点需要注意:CNN处理的图像或者视频数据中像素点(pixel)是排列成成很整齐的矩阵。(欧几里得距离Euclidean Structure)
与之相对应,科学研究中还有很多Non Euclidean Structure的数据,如图3所示。社交网络、信息网络中有很多类似的结构。
Graph Convolutional Network中的Graph是指数学(图论)中的用顶点和边建立相应关系的拓扑图。
那么为什么要研究GCN?
原因有三:
1)CNN无法处理Non Euclidean Structure的数据,学术上的表达是传统的离散卷积(如问题1中所述)在Non Euclidean Structure的数据上无法保持平移不变性。通俗理解就是在拓扑图中每个顶点的相邻顶点数目都可能不同,那么当然无法用一个同样尺寸的卷积核来进行卷积运算。 (所谓的欧氏(欧几里德)数据指的是类似于grids, sequences… 这样的数据,例如图像就可以看作是2D的grid数据,语音信号就可以看作是1D的grid数据。但是现实的处理问题当中还存在大量的 Non-Euclidean Data,如社交多媒体网络(Social Network)数据,化学成分(Chemical Compound)结构数据,生物基因蛋白(Protein)数据以及知识图谱(Knowledge Graphs)数据等等,这类的数据属于图结构的数据(Graph-structured Data)。CNN等神经网络结构则并不能有效的处理这样的数据,可以参考https://www.leiphone.com/news/201706/ppA1Hr0M0fLqm7OP.html)
2)由于CNN无法处理Non Euclidean Structure的数据,又希望在这样的数据结构(拓扑图)上有效地提取空间特征来进行机器学习,所以GCN成为了研究的重点。
3)读到这里大家可能会想,自己的研究问题中没有拓扑结构的网络,那是不是根本就不会用到GCN呢?其实不然,广义上来讲任何数据在赋范空间内都可以建立拓扑关联,谱聚类就是应用了这样的思想(谱聚类(spectral clustering)原理总结)。所以说拓扑连接是一种广义的数据结构,GCN有很大的应用空间。 综上所述,GCN是要为除CV、NLP之外的任务提供一种处理、研究的模型。
3 提取拓扑图空间特征的两种方式 GCN的本质目的就是用来提取拓扑图的空间特征,那么实现这个目标只有graph convolution这一种途径吗?
当然不是,在vertex domain(spatial domain)和spectral domain实现目标是两种最主流的方式。
(1)vertex domain(spatial domain)是非常直观的一种方式。顾名思义:提取拓扑图上的空间特征,那么就把每个顶点相邻的neighbors找出来。
这里面蕴含的科学问题有二:
a.按照什么条件去找中心vertex的neighbors,也就是如何确定receptive field?
b.确定receptive field,按照什么方式处理包含不同数目neighbors的特征?
根据a,b两个问题设计算法,就可以实现目标了。推荐阅读这篇文章Learning Convolutional Neural Networks for Graphs(图4是其中一张图片,可以看出大致的思路)。

这种方法主要的缺点如下: c.每个顶点提取出来的neighbors不同,使得计算处理必须针对每个顶点 d.提取特征的效果可能没有卷积好
(2)spectral domain就是GCN的理论基础了。这种思路就是希望借助图谱的理论来实现拓扑图上的卷积操作。
从整个研究的时间进程来看:首先研究GSP(graph signal processing)的学者定义了graph上的Fourier Transformation,进而定义了graph上的convolution,最后与深度学习结合提出了Graph Convolutional Network。 认真读到这里,脑海中应该会浮现出一系列问题: Q1 什么是Spectral graph theory? Spectral graph theory请参考这个,简单的概括就是借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质 Q2 GCN为什么要利用Spectral graph theory? 这应该是看论文过程中读不懂的核心问题了,要理解这个问题需要大量的数学定义及推导,没有一定的数学功底难以驾驭(我也才疏学浅,很难回答好这个问题)。 所以,先绕过这个问题,来看Spectral graph实现了什么,再进行探究为什么?
4 什么是拉普拉斯矩阵?为什么GCN要用拉普拉斯矩阵?
Graph Fourier Transformation及Graph Convolution的定义都用到图的拉普拉斯矩阵,那么首先来介绍一下拉普拉斯矩阵。 对于图 G=(V,E),其Laplacian 矩阵的定义L=D-A ,其中 L是Laplacian 矩阵, D是顶点的度矩阵(对角矩阵),对角线上元素依次为各个顶点的度, A是图的邻接矩阵。看图5的示例,就能很快知道Laplacian 矩阵的计算方法。

常用的拉普拉斯矩阵实际有三种:
No.1 L=D-A 定义的Laplacian 矩阵更专业的名称叫Combinatorial Laplacian
No.2 Lsys=D(-1/2)LD^(-1/2)定义的叫Symmetric normalized Laplacian,很多GCN的论文中应用的是这种拉普拉斯矩阵
No.3 Lrw=D(-1)L定义的叫Random walk normalized Laplacian,有读者的留言说看到了Graph Convolution与Diffusion相似之处,当然从Random walk normalized Laplacian就能看出了两者确有相似之处(其实两者只差一个相似矩阵的变换
为什么GCN要用拉普拉斯矩阵?
拉普拉斯矩阵矩阵有很多良好的性质,这里写三点我感触到的和GCN有关之处
(1)拉普拉斯矩阵是对称矩阵,可以进行特征分解(谱分解),这就和GCN的spectral domain对应上了
(2)拉普拉斯矩阵只在中心顶点和一阶相连的顶点上(1-hop neighbor)有非0元素,其余之处均为0
(3)通过拉普拉斯算子与拉普拉斯矩阵进行类比(详见第6节)
5 拉普拉斯矩阵的谱分解(特征分解)
GCN的核心基于拉普拉斯矩阵的谱分解,文献中对于这部分内容没有讲解太多,初学者可能会遇到不少误区,所以先了解一下特征分解。
矩阵的谱分解,特征分解,对角化都是同一个概念(特征分解_百度百科)。
不是所有的矩阵都可以特征分解,其充要条件为n阶方阵存在n个线性无关的特征向量。
但是拉普拉斯矩阵是半正定对称矩阵(半正定矩阵本身就是对称矩阵,半正定矩阵_百度百科,此处这样写为了和下面的性质对应,避免混淆),有如下三个性质:
对称矩阵一定n个线性无关的特征向量
半正定矩阵的特征值一定非负
对阵矩阵的特征向量相互正交,即所有特征向量构成的矩阵为正交矩阵。
由上可以知道拉普拉斯矩阵一定可以谱分解,且分解后有特殊的形式。 对于拉普拉斯矩阵其谱分解为:

6 如何从传统的傅里叶变换、卷积类比到Graph上的傅里叶变换及卷积?
把传统的傅里叶变换以及卷积迁移到Graph上来,核心工作其实就是把拉普拉斯算子的特征函数 e^(-iwt)变为Graph对应的拉普拉斯矩阵的特征向量。
(1)推广傅里叶变换
(a)Graph上的傅里叶变换



2)推广卷积 在上面的基础上,利用卷积定理类比来将卷积运算,推广到Graph上。 卷积定理:函数卷积的傅里叶变换是函数傅立叶变换的乘积,即对于函数 与 两者的卷积是其函数傅立叶变换乘积的逆变换:


7 为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基?特征值表示频率?
(1)为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基? 傅里叶变换一个本质理解就是:把任意一个函数表示成了若干个正交函数(由sin,cos 构成)的线性组合。

8 Deep Learning中的Graph Convolution
Deep learning 中的Graph Convolution直接看上去会和第6节推导出的图卷积公式有很大的不同,但是万变不离其宗,(1)式是推导的本源。
第1节的内容已经解释得很清楚:Deep learning 中的Convolution就是要设计含有trainable共享参数的kernel,从(1)式看很直观:graph convolution中的卷积参数就是diag(h^(lamad_l))

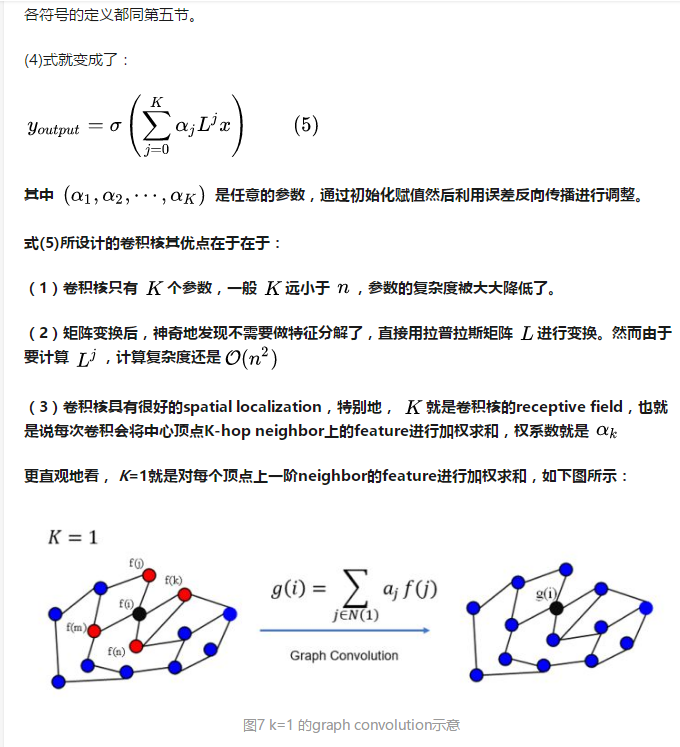
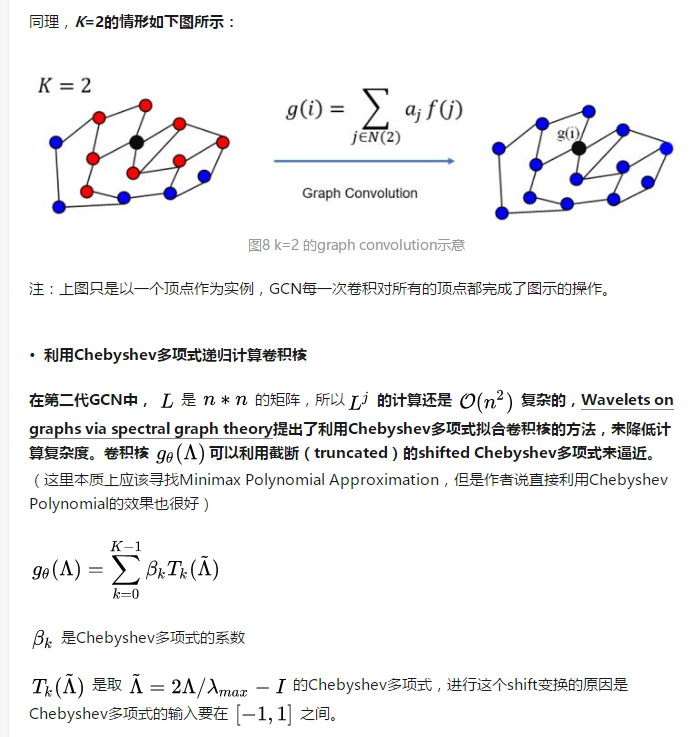

9 在GCN中的Local Connectivity和Parameter Sharing
CNN中有两大核心思想:网络局部连接,卷积核参数共享。
https://link.zhihu.com/?target=https%3A//www.sciencedirect.com/science/article/pii/S0968090X18315389%3Fdgcid%3Dcoauthor

12 GCN的相关资料
——————GCN的综述与论文合辑
https://mp.weixin.qq.com/s/WW-URKk-fNct9sC4bJ22eg
https://mp.weixin.qq.com/s/3CYkXj2dnehyJSPLBTVSDg
观点2:
先说问题的本质:图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡,关系越亲近的邻居影响越大。 要想理解GCN以及其后面一系列工作的实质,最重要的是理解其中的精髓Laplacian矩阵在干什么。知道了Laplacian矩阵在干什么后,剩下的只是解法的不同——所谓的Fourier变换只是将问题从空域变换到频域去解,所以也有直接在空域解的(例如GraphSage)。

同理,在高维的欧氏空间中,一阶导数就推广到梯度,二阶导数就是我们今天讨论的主角——拉普拉斯算子:

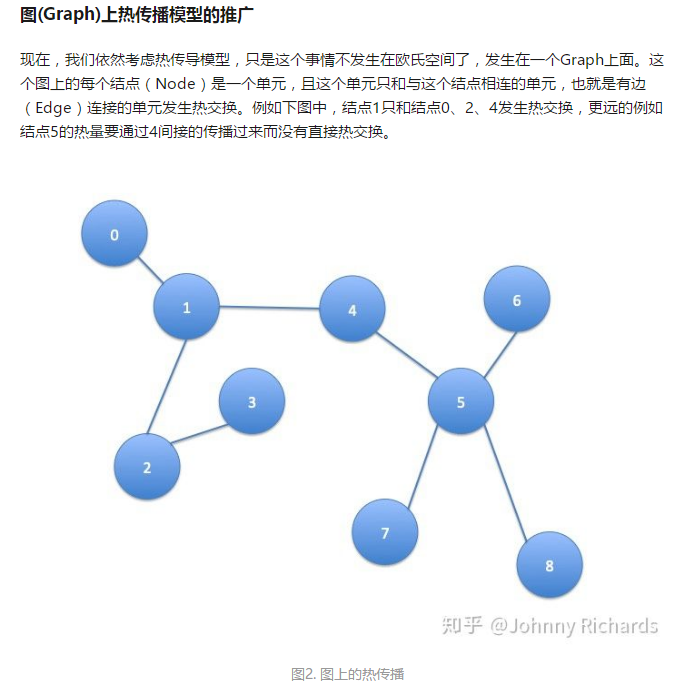




恒温热源的存在,正是我们跨向半监督学习的桥梁。 我们把问题向广告和推荐场景去类比,在这个场景下,某些结点有着明确的label,例如某个广告被点击,某个广告的ctr是多少,某个item被收藏,这些带着label的结点有着相对的确定性——它们可以被看作是这个结点的温度,这些有标签的结点正是恒温热源。那么,这些图的其他参与者,那些等待被我们预测的结点正是这张图的无源部分,它们被动的接受着那些或近或远的恒温热源传递来的Feature,改变着自己的Feature,从而影响自己的label。 让我们做个类比: 温度 好比 label 是状态量 恒温热源 好比 有明确 label的结点,它们把自己的Feature传递给邻居,让邻居的Feature与自己趋同从而让邻居有和自己相似的label 结点的热能就是Feature,无标签的、被预测的结点的Feature被有明确label的结点的Feature传递并且影响最终改变自己 需要说明的一点是,无论是有源还是无源,当有新的结点接入已经平衡的系统,系统的平衡被打破,新的结点最终接受已有结点和恒温热源的传递直到达到新的平衡。所以我们可以不断的用现有的图去预测我们未见过的结点的性质,演化和滚大这个系统。