高维前缀和略解

\[made\ by\ Ameiyo \]

前言

似乎我们教练也说是叫高维前缀和。。。

那么高位前缀和又是什么呢。。。

算了这些是题外话。

关于高维前缀和：

目前看来可以用于 $ DP $ 的优化，但是有一定的局限性。

若对于所有的状态 $ S $ ，其需要向 $ S' $ 贡献答案，在这里我们称 $ S' $ 为 $ S $ 的父亲， $ S $ 为 $ S' $ 的子孙。

高维前缀和的使用条件:

(这个条件其实无视也无所谓，因为是我自己根据证明方法胡诌的。换句话说，如果证明方法，或者说更新方法不一样，约束也就不一样了)

(1) $ S' $ 的父亲必是其子孙 $ S $ 的父亲之一。

(2) $ S $ 到其某个父亲的 $ S' $ 的转移路径或是直接转移，或是能通过其他直接转移一个个转移上去，并且中间的状态必是 $ S $ 的父亲。

(3) 父子关系不能有环。

从上述第三点也可以看出状态的转移满足无后效性，所以高维前缀和往往是对 $ DP $ 的优化。

loop d : // 遍历所有直接转移
	loop S : // 遍历所有状态
		if (check(S + d)) dp(S + d) += dp(S) // 如果合法，更新

而 $ DP $ 的做法往往是这样:

loop S : // 遍历所有的状态
	loop D : // 遍历所有转移，包括间接转移
		if (check(S + d)) dp(S + d) += val(S) // 如果合法，更新

这个代码看起来没有 $ DP $ 的样子，实际上他可能是某个 $ DP $ 的内层，这个时候优化可能就很有用了。

对比两份代码，我们会发现高位前缀和对时间的优化主要是针对转移。相当于是把大的转移拆分成小的互不干扰的转移，这种优化实际上有一个很经典的实例—— 多重背包的二进制优化 。

在理解时，可以借助二进制优化来思考。

更详细的讲解

为了更好的理解，这里先使用较常用的二进制表示集合(状态)的方法来做例子。(没错就是刷状压时遇到的QAQ)

先看一道题。

CodeChef MAXOR: Good Pairs

(这里给出的是 $ vjudge $ 链接)

You are given $ N $ integers: $ A_1 $ , $ A_2 $, ..., $ A_N $ . You need to count the number of pairs of indices $ (i, j) $ such that $ 1 \leq i < j \leq N $ and $ A_i | A_j \leq max(A_i, A_j) $ .

给你 $ n $ 个数，每个数是 $ A_i $ ,求有多少对 $ (i, j) $ ，满足 $ A_i | A_j \leq max(A_i, A_j) $ 。

$ 1 \leq N \leq 10 ^ 6 $

$ 0 \leq A_i \leq 10 ^ 6 $

$ 1 \leq Sum\ of\ N\ over\ all\ test\ cases \leq 10 ^ 6 $

因为 $ x\ |\ y\ \geq x $ ，所以满足 $ A_i\ |\ A_j \leq max( A_i,\ A_j ) $ 就相当于 $ A_i\ |\ A_j\ =\ max(A_i,\ A_j ) $ 。在 $ A_i \leq A_j $ 的时候就相当于 $ A[i] $ 的二进制表示法是 $ A_j $ 的子集(被包含)。

我们用 $ f[i] $ 表示二进制表示法下是 $ i $ 的子集的数的个数，其中有 $ g[i] $ 个于 $ i $ 相同。

那么 $ i $ 对 $ Ans $ 的贡献就是

\[g[i] \cdot (g[i] - 1) / 2 + (f[i] - g[i]) \cdot g[i] \]

重点就是 $ f[i] $ 的统计。

如果是普通的枚举，那么复杂度将会达到 $ O( \Sigma C_n ^ k \cdot 2 ^ k ) $ ， $ n $ 可以达到 $ 20 $，这会是 $ TLE $ 级别的复杂度(不想算。。但是在 $ k = 10 $ 的时候就已经有亿万级别了)。

(复杂度的计算是这样的，每个状态被自己的所有子集更新一次，子集个数是 $ 2 ^ k $ ，$ k $ 是状态中 $ 1 $ 的个数。那么 $ 1 $ 的个数是 $ k $ 的状态个数是 $ C_n ^ k $ ，也就是上述的那样。在 $ k = 10,\ n = 20 $ 时，大小为 $ 189190144 $ )

我应该没算错QAQ。

所以我们需要用到高位前缀和。

初始时 $ f[i] = g[i] $ ，然后

loop i from 0 to 21 : // 枚举直接转移(通过某一位上的1)
	loop S from Maxn to 0 : // 枚举状态
		if (S & (1 << i)) dp(S) += dp(S ^ (1 << i)) // 如果可以更新

注意枚举转移放在了外层循环，而不是内层，否则就会重复许多。

下面证明这样子对于所有的 $ S $ 而言，更新到了其全部的父亲并且没有重复更新。

这里我们建一个图，当且仅当$ S $ 能通过改变一个 $ 0 $ 为 $ 1 $ 变为 $ S' $ 时，从 $ S $ 为起点，向 $ S' $ 连边，于是一条边就对应着代码里的一次转移。

比如说 $ 000 $ 可以向 $ 010, 001, 100 $ 连边，但是不能向 $ 011 $ 连边，因为它改变了两个 $ 0 $ 为 $ 1 $ 。

那么，$ 3 $ 位的图就是这个样子

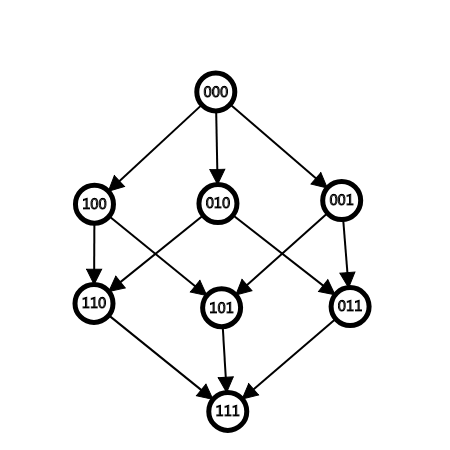
3位01的树.png

这张图也可以很好的解释为什么在内层循环枚举转移会重复，因为每次把每个状态的所有边同时走了一遍。

可以发现在每一层的节点中， $ 1 $ 的个数都是相同的，并且上下两层呈递增关系。

每走一条边，就对应着代码里一次更新，也就是相当于把 到达过 当前状态 $ S $ 的点累积到 $ S' $ 中。

(用“到达过”是因为加了之后不会去掉)

对于某个 $ S $ 及其任意一个父亲 $ S' $ ，设 $ t = S' - S $ ，也就是二者的差。

假设 $ t $ 中 $ 1 $ 的个数为 $ cnt $ ，那么 $ S $ 需要走 $ cnt $ 条边才能到达 $ S' $ 。

$ t $ 里面包括的 $ 1 $ 的种类(哪一位上的 $ 1 $ )是固定的，也就是说 $ S $ 只有在经过且只经过 $ t $ 里面所有的 $ 1 $ 后才会到达 $ S' $。

比如说按照代码，三位的转移如下:

转移的1 \ 结点	000	001	010	100
初始	000	001	010	100
经过001的更新	000	000,001	010	100
经过010的更新	000	000,001	000,010	100
经过100的更新	000	000,001	000,010	000,100
---	---	---	---	---
转移的1 \ 结点	011	101	110	111
初始	011	101	110	111
经过001的更新	010,011	100,101	110	110,111
经过010的更新	$ \ $ 000,001,010,011	100,101	100,110	$ \ $ 100,101,110,111
经过100的更新	$ \ $ 000,001,010,011	$ \ $ 000,001,100,101	$ \ $ 000,010,100,110	$ \ $ 000,001,010,100,011,101,110,111

而走的边的种类是按顺序枚举的，也就是说 $ S $ 到 $ S' $ 的路径用边来描述是一个有序数列，既然顺序固定，边的种类又没有变化，那么这个数列是唯一的。也就是说 $ S $ 按照代码只会在一种 转移的集合 中更新到 $ S' $ 。也就是不会重复更新。

而既然每条路径都是存在的，也就是 $ t $ 是必然能通过一种序列满足的，也就是说这个数列是必然存在的，那么对于 $ S $ 所有的父亲而言，对应的 $ t $ 都是有对应的 符合代码的转移路径 的，即所有的父亲都会更新到。

个人认为可能有一点抽象，还不懂得同学可以手动模拟一下，记录当前状态下的 $ dp $ 数组包含了那些点，然后顺着每次挑一种边累加下去。。。(可以对着上面的表格)

这种模拟的方法可以帮助你很大程度上理解算法，然后看证明可能会更容易看懂。如果还没有看懂可以 $ QQ $ (1134406557)找我。

然后回到这道题。

解析前面也说的很详细了，裸的高维前缀和就行，直接上代码吧。

n = read<int>();
for (reg int i = 1, x; i <= n; ++i) {
	x = read<int>();
	++f[x], ++g[x];
}
for (reg int i = 0; i < 21; ++i)
	for (reg int j = 0; j <= N - 5; ++j)
		if (j & (1 << i)) f[j] += f[j ^ (1 << i)];
ll Ans = 0;
for (reg int i = 0; i <= N - 5; ++i) {
	if (g[i]) {
		Ans += g[i] * (g[i] - 1) / 2;
		Ans += g[i] * (f[i] - g[i]);
	}
}
cout << Ans << endl;

(注意多组数据别忘记清零)

条件的进一步提炼

这里再来看一看高维前缀和使用的条件，借助证明把他提取出来。

我们会注意到证明中很重要的一点，那就是 转移的路径 。事实上，只要保证了按照代码的运行，转移的路径 只有一条并且一定存在 就满足了必定更新与不重复更新，也就保证了答案的正确性。

(事实上就是对上述三条的总结QAQ)

无环就是显然的只有一条路径的必要条件，也即无后效性。

也就是说，高维前缀和的使用与否可能是取决于代码，甚至是对数组意义的定义。