钢条切割问题求解方法及相关思考
题目来源于《算法导论》第15章第一节。问题如下:
给定一个长度为n英寸的钢条和一个价格表pi(i=1,2,3,...n),求能够使销售收益rn最大的切割方案。
问题1:一共有多少种切割方式?
思路一:对于一个长度为n英寸的钢条,其中一共有n-1个节点可供切割,在每一个节点处都可以选择切割或者不切割,将对一根钢条的切割过程视为从第一个节点直到第n-1个节点逐一选择切割或者不切割的一个过程,利用乘法原理,可以算出来总共有2n-1种切割方案。以四个节点的钢条为例:
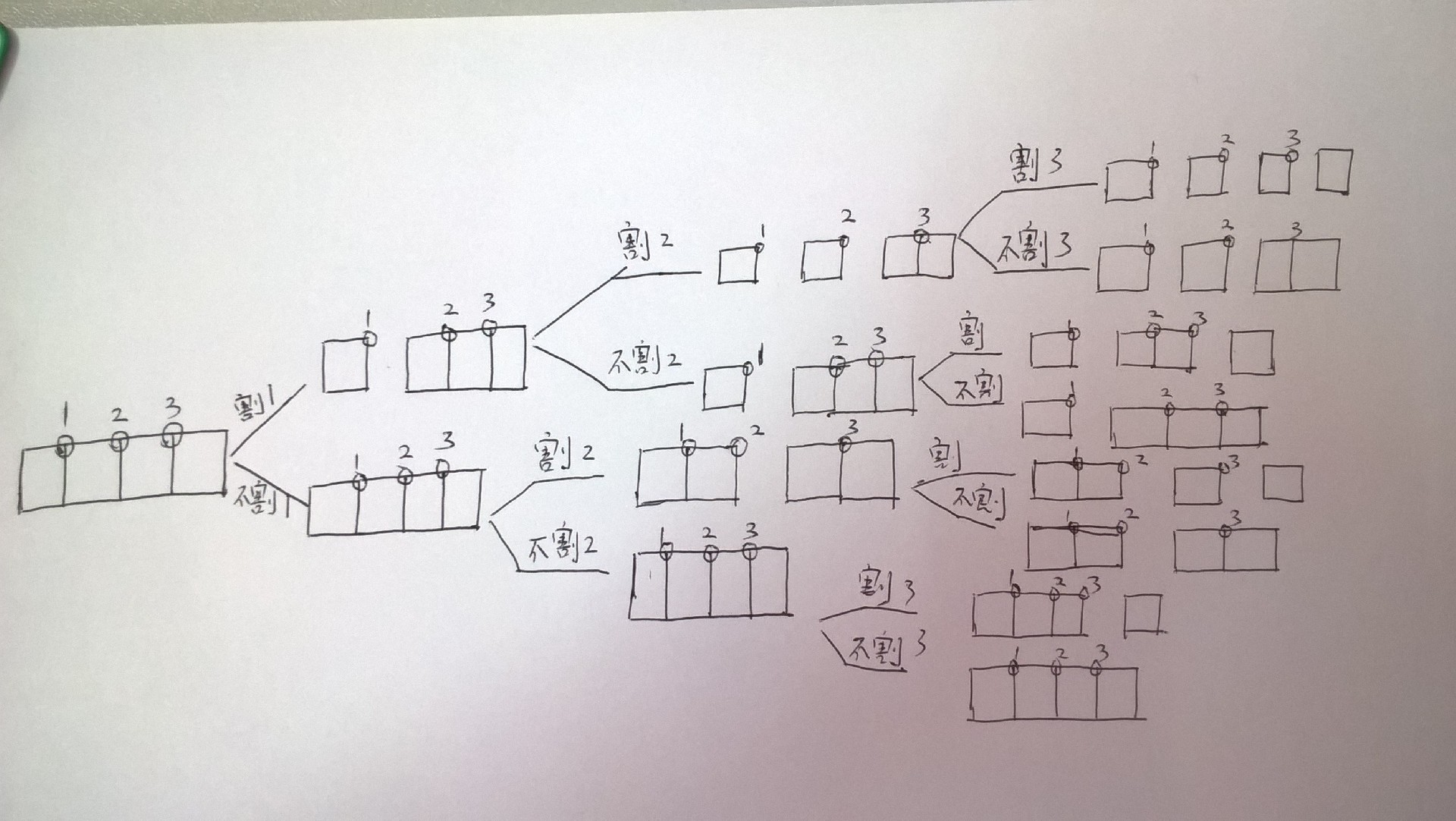
思路二:也可以将切割一个长度为n英寸的钢条视作是从n-1个节点当中选择i(i=0,1,2,....,n-1)个节点进行分割的过程。那么总的分割方式m的计算方式可以使用排列组合的相关知识进行运算。m=C0n-1+C1n-1+.....+Cn-1n-1,根据牛顿二项式公式m=2n-1。
问题解决方案
一、自顶向下递归
从钢条左边切割下长度为i的一段(不作任何处理),再对剩下的长度为n-i的钢条进行切割(递归),一个最优的解决方案就是:rn=max(pi+rn-i)(1<=i<=n),C++代码实现如下:
1 #include "stdafx.h" 2 int CutRod(int p[], int n)//输入分别为价格数组和问题规模(钢条大小) 3 { 4 if (n == 0) 5 { 6 return 0; 7 } 8 int q = -1000;//保证程序的顺利启动 9 for (int i = 1; i <= n; i++) 10 { 11 if (q < p[i - 1] + CutRod(p, n - i)) 12 { 13 q=p[i - 1] + CutRod(p, n - i); 14 } 15 } 16 return q; 17 } 18 int _tmain(int argc, _TCHAR* argv[]) 19 { 20 int a[10] = { 1, 5, 8, 9, 10, 17, 17, 20, 24, 25 };//钢条分割的价格数组 21 printf("%d", CutRod(a, 10)); 22 getchar(); 23 return 0; 24 }
问题2:这样的一种递归遍历能否遍历所有的2n-1种切割方法?
我之前一直以为这种计算方法无法遍历到所有的切割方式,以为这种每一次都不考虑左半边分割的方式会忽略掉某些解。但是细想的话会发现,原来对于左半边的分割在之前的遍历当中已经考虑到了,并不需要再考虑。比如,如果从距离钢条左边2英寸处分割成两半然后只考虑右边的n-2英寸的钢条的分割的话,不需要考虑将左边2英寸的钢条再分为两个1英寸的情况,因为在计算将左边分为一个1英寸这种情况的时,另外的n-1部分其中有一种情况就是将其分为一个1寸和n-2寸的情况,这样就考虑了之前所说的那种情况。也可以对比问题一当中的例子来思考这一问题。
二、利用动态规划的思想解决这一问题
上面所提到的那种算法会在遍历的过程当中多次计算同样的子问题,所以需要应用一些策略来减少算法计算数量,下面分别提供了两种更好的方案。
带备忘的自顶向下的解决方案:记录在遍历的过程当中所遇到的子问题的解,算法在后面的运行当中会对照所记录的解,如果当前子问题存在解就直接输出解,否则就执行运算;
自底向上的解决方案:先解决子问题,再利用子问题的解来解决父问题;
1、带备忘的自顶向下的解决方案C++实现
此程序还可以记录下每一个子问题的最佳切割方案,最后输出问题整个问题的最佳切割过程。
1 #include "stdafx.h" 2 #include <string> 3 using namespace std; 4 struct A{ 5 int q; 6 int* r; 7 int* step; 8 }; 9 //有备忘的自顶向下解决方案 10 //对规模为n的问题进行计算 11 int MCutRodA(int a[], int n, int r[],int step[]) 12 { 13 int q;//问题的解 14 int s;//切割方案 15 if (r[n] >= 0)//如果子问题已经有解就返回所记录的子问题的解 16 { 17 return r[n]; 18 } 19 if (n == 0) 20 { 21 q = 0; 22 s = 0; 23 } 24 else{ 25 q = -100; 26 for (int i = 1; i <= n; i++) 27 { 28 if (q < MCutRodA(a, n - i, r,step) + a[i-1]) 29 { 30 q = MCutRodA(a, n - i, r, step) + a[i - 1]; 31 s = i; 32 } 33 } 34 } 35 r[n] = q;//记录解 36 step[n] = s;//记录切割方案 37 return q; 38 } 39 //带备忘的递归解决方案 40 A MCutRod(int a[],int n) 41 { 42 int* r = (int*)malloc((n + 1)*sizeof(int));//设置一个数组记录不同规模的子问题的解 43 int* step = (int*)malloc((n + 1)*sizeof(int));//设置一个数组记录不同规模子问题的切割方案 44 for (int i = 0; i <= n; i++) 45 { 46 r[i] = -1; 47 } 48 A B; 49 B.q = MCutRodA(a, n, r, step); 50 B.r = r; 51 B.step = step; 52 return B; 53 } 54 int _tmain(int argc, _TCHAR* argv[]) 55 { 56 int a[10] = { 1, 5, 8, 9, 10, 17, 17, 20, 24, 25 };//钢条分割的价格数组 57 A B = MCutRod(a, 10); 58 printf("不同子问题的最大价值:"); 59 for (int i = 0; i < 11; i++) 60 { 61 printf("%d ", B.r[i]); 62 } 63 printf(" 不同规模子问题从左边开始的最优切割方式:"); 64 for (int i = 0; i < 11; i++) 65 { 66 printf("%d ", B.step[i]); 67 } 68 printf(" "); 69 printf("%d", B.q); 70 int n = 10; 71 printf("最佳的切割方式为:"); 72 while (n > 0) 73 { 74 printf("%d ", B.step[n]); 75 n = n - B.step[n]; 76 } 77 getchar(); 78 return 0; 79 }
2、自底向上解决方案的C++实现
1 int BTUCutRod(int a[], int n) 2 { 3 int* r = (int*)malloc((n + 1)*sizeof(int)); 4 r[0] = 0; 5 for (int i = 1; i <= n; i++)//遍历所有可能的问题规模数 6 { 7 int q = -100; 8 for (int j = 1; j <= i; j++) 9 { 10 if ((a[j - 1] + r[i - j]) > q) 11 { 12 q = a[j - 1] + r[i - j]; 13 } 14 } 15 r[i] = q; 16 } 17 return r[n]; 18 } 19 int _tmain(int argc, _TCHAR* argv[]) 20 { 21 int a[10] = { 1, 5, 8, 9, 10, 17, 17, 20, 24, 25 };//钢条分割的价格数组 22 printf("%d", BTUCutRod(a, 10)); 23 getchar(); 24 return 0; 25 }