题目
给一棵 (n) 个点的树,每个点有体积 (a_i) 和价值 (b_i),求总容量为 ([1,m]) 时选出一个最大价值独立集(相邻节点不能同时选)的方案数。
(nle 50,mle 5000)。
解法
( ext{dfs}) 序优化树形背包。
在讲这道题之前,先讲一下 另一道题。
令 (f[i][j]) 为 ( ext{dfs}) 序为 (i) 的点和 ( ext{dfs}) 序比它大的点选 (j) 门课的最大得分。则有:
即跳过这棵子树和 可以 选择这棵子树。注意后面的情况可能会到另一棵子树,这就相当于选了 (i) 这个单点。
这样按 ( ext{dfs}) 序倒序转移即可。
好了回到这道题。
先考虑朴素 (mathtt{DP})。令 (f[i][j][0/1]) 为当前点 (i),已选 (j) 体积,是否选 (i) 的最大价值方案数,这是 (mathcal O(nm^2)) 的。
这里再提一句,有一种树形背包时间复杂度可以被证明是 (mathcal O(nm)) 的,不过这道题没有 (siz) 的限制,所以证明不成立。
我们可以用 ( ext{dfs}) 序优化。但很快发现一个问题,如下图(图源 ( ext{lhm_liu})):
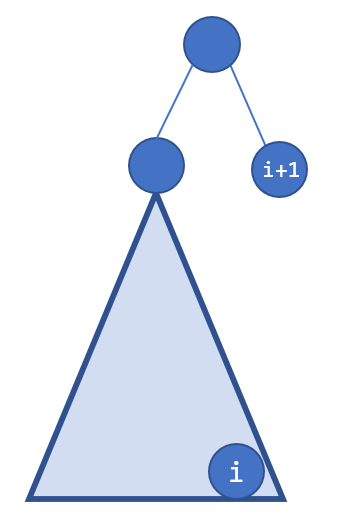
从 (i ightarrow i+1) 的过程,你并不知道 (i+1) 是否可选。
思考为什么上面那道题可以这么做?上面那道题在父节点就可以判断是否可取(不取就整棵子树都不取),所以本身就可以随便算。而这道题取了只会导致儿子与父亲不可取,如果只考虑儿子显然是需要枚举的,这就破坏了复杂度。
那怎么办呢?首先可以想到再加一维状态表示是否选取,不过 (2^{50}) 显然挂了。
仔细思考,先令类似 (i+1) 的父亲的点为关键点。那么,对于 (u),它的最后一个遍历的子树不用添加 (u) 为关键点,因为 (u) 的子树之后已经遍历完了(很类似 ( ext{CodeForces - 600E Lomsat gelral}))。
那么我们重链剖分,将重链放到最后遍历。容易发现,点 (i) 包含的关键点就是 (i) 到根每条链的链顶,这样就是 (2^{log n}=n) 的。
单次复杂度 (mathcal O(n^2 m))。
代码
#include <cstdio>
#define rep(i,_l,_r) for(register signed i=(_l),_end=(_r);i<=_end;++i)
#define fep(i,_l,_r) for(register signed i=(_l),_end=(_r);i>=_end;--i)
#define erep(i,u) for(signed i=head[u],v=to[i];i;i=nxt[i],v=to[i])
#define efep(i,u) for(signed i=Head[u],v=to[i];i;i=nxt[i],v=to[i])
#define print(x,y) write(x),putchar(y)
template <class T> inline T read(const T sample) {
T x=0; int f=1; char s;
while((s=getchar())>'9'||s<'0') if(s=='-') f=-1;
while(s>='0'&&s<='9') x=(x<<1)+(x<<3)+(s^48),s=getchar();
return x*f;
}
template <class T> inline void write(const T x) {
if(x<0) return (void) (putchar('-'),write(-x));
if(x>9) write(x/10);
putchar(x%10^48);
}
template <class T> inline T Max(const T x,const T y) {if(x>y) return x; return y;}
template <class T> inline T Min(const T x,const T y) {if(x<y) return x; return y;}
template <class T> inline T fab(const T x) {return x>0?x:-x;}
template <class T> inline T gcd(const T x,const T y) {return y?gcd(y,x%y):x;}
template <class T> inline T lcm(const T x,const T y) {return x/gcd(x,y)*y;}
template <class T> inline T Swap(T &x,T &y) {x^=y^=x^=y;}
#include <vector>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn=55,maxm=5005;
int n,m,a[maxn],b[maxn],pos,siz[maxn],son[maxn],dfn[maxn],idx,f[maxn],tp[maxn],app[maxn];
vector <int> e[maxn],fa[maxn];
struct node {
int val; ll cnt;
node operator + (const int Val) {
return (node){val+Val,cnt};
}
node operator + (const node t) {
if(val<t.val) return t;
else if(val==t.val) return (node){val,cnt+t.cnt};
return *this;
}
} g[2][maxn][maxm],ans[maxm];
void dfs1(int u,int fa) {
siz[u]=1; f[u]=fa;
for(int i=0;i<e[u].size();++i) {
int v=e[u][i];
if(v==fa) continue;
dfs1(v,u);
siz[u]+=siz[v];
if(siz[son[u]]<siz[v]) son[u]=v;
}
}
void dfs2(int u,int t) {
tp[u]=t,dfn[++idx]=u;
for(int i=0;i<e[u].size();++i) {
int v=e[u][i];
if(v==f[u] || v==son[u]) continue;
dfs2(v,v);
}
if(son[u]) dfs2(son[u],t);
}
void init() {
idx=0;
memset(g,0,sizeof g);
rep(i,1,n)
e[i].clear(),fa[i].clear(),
son[i]=0;
rep(i,1,m) ans[i]=(node){0,0};
}
int main() {
int u,v,Father,S,Case=read(9),T=Case;
for(;T;--T) {
n=read(9),m=read(9); init();
rep(i,1,n) a[i]=read(9),b[i]=read(9);
rep(i,1,n-1) u=read(9),v=read(9),e[u].push_back(v),e[v].push_back(u);
dfs1(1,0); dfs2(1,1);
rep(i,1,n) {
u=i;
fa[i].push_back(i);
while(f[tp[u]]) u=f[tp[u]],fa[i].push_back(u);
}
g[0][0][0]=(node){0,1};
rep(i,1,n) {
pos=i&1;
rep(s,0,(1<<fa[dfn[i]].size())-1) rep(j,0,m) g[pos][s][j]=(node){0,0};
Father=10;
for(int j=0;j<fa[dfn[i-1]].size();++j) {
u=fa[dfn[i-1]][j];
if(u==f[dfn[i]]) Father=j;
app[j]=-1;
for(int k=0;k<fa[dfn[i]].size();++k)
if(u==fa[dfn[i]][k]) app[j]=k;
}
rep(s,0,(1<<fa[dfn[i-1]].size())-1) {
S=0;
for(int j=0;j<fa[dfn[i-1]].size();++j)
if((s>>j&1) && (~app[j])) S|=(1<<app[j]);
rep(j,0,m) {
if(!g[pos^1][s][j].cnt) continue;
g[pos][S][j]=g[pos][S][j]+g[pos^1][s][j];
if((s>>Father&1) || j+a[dfn[i]]>m) continue;
g[pos][S|1][j+a[dfn[i]]]=g[pos][S|1][j+a[dfn[i]]]+(g[pos^1][s][j]+b[dfn[i]]);
}
}
}
rep(i,0,(1<<fa[dfn[n]].size())-1) rep(j,0,m) ans[j]=ans[j]+g[pos][i][j];
printf("Case %d:
",Case-T+1);
rep(i,1,m) print(ans[i].cnt,i==m?'
':' ');
}
return 0;
}