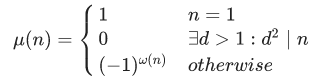1. 定义
若函数 (f(n)) 满足 (f(1)=1) 且当 (x,y) 均为正整数且 (gcd(x,y)=1) 时,都有
[f(xy)=f(x)f(y)
]
则 (f(n)) 为积性函数。
特别地,当不满足 (gcd(x,y)=1) 仍有上式满足时,称 (f(n)) 为完全积性函数。
2. 性质

证明第四个柿子:
[h(x)h(y)=sum_{i|x}f(i)g(frac{x}{i})sum_{j|y}f(j)g(frac{y}{j})
]
因为 (gcd(x,y)=1),我们将 (i,j) 直接两两组合显然 (i imes j) 是不重的。
3. 常见积性函数
-
单位函数:(epsilon(n)=[n=1])(完全积性)。
-
恒等函数:( ext{id}(n)=n)(完全积性)。
-
除数函数:(sigma_x(n)=sum_{d|n}d^x)。
当 (x=0) 时,可简写成 ( au(n), ext d(n))。
当 (x=1) 时,可简写成 (sigma(n))。 -
欧拉函数:(varphi(n)=sum_{i=1}^n[gcd(i,n)=1])。戳这。
另外 (sum_{i=1}^n[gcd(i,n)=1] imes i) 可化成 (frac{n imes varphi(n)}{2}+frac{[n=1]}{2})。证明。
一个小优化:预处理 (sqrt n) 中的质数,对于每个 (x) 直接枚举质数,单次是 (mathcal O(frac{sqrt n}{ln n}))(质数个数)。
-
莫比乌斯函数(其中 (omega(n)) 是 (n) 本质不同质因子个数):