0. 前置芝士
0.1. 复数
0.1.1. 定义
形如 (z=a+bi)((a,b) 均为实数)的数称为复数,其中 (a) 称为实部,(b) 称为虚部。其中 (i) 是虚数单位,满足 (i^2=-1)。
另外,可以将其想象成平面直角坐标系上的点/向量 ((a,b))。
定义 ( heta) 为复数 (z) 的辐角(由上可想象),(r=sqrt{a^2+b^2}) 是模长。
那么 (z) 可以表示为 (r imes (cos heta+isin heta))(显然 (r imes cos heta) 就是 (a))。
还可以用欧拉公式((e^{xi}=cos x+isin x))表示:(z=r imes e^{xi})。
不过下文就会省略 (r)(因为是单位圆)。
0.1.2. 计算
相加/减就是实部与虚部相加/减。
相乘就是 (z_1z_2=r_1 imes r_2 imes e^{(x+y)i}),即 模长相乘,幅角相加。
这里再提一嘴,如果想让复数转动一定角度,我们只用乘上此角度对应的 单位复数 以保障模长不变。
0.2. 多项式表示法
0.2.1. 系数多项式
0.2.2. 点值多项式
选取 (n) 个 (x_i) 代入 (f(x)) 得到 (y_i),每一对表示为 ((x_i,y_i))。因为 (n) 个未知系数 (a_i) 需要 (n) 个方程即可解。
0.3. 单位复根
0.3.1. 定义
由欧拉公式可知,(e^{xi}) 对应的复数的辐角为 (x)(弧度制),故 (e^{2pi i}) 对应 (2pi)。
假设我们需要把 (2pi) 分成 (n) 等份(如下图,(n=8)),设一份对应着 (omega_n)。
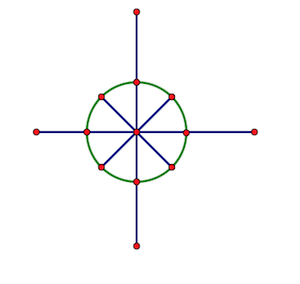
我们需要将 (omega_n) 的辐角加 (n-1) 个它本身才是 (2pi)。
想到什么了吗?相乘即是模长相乘,幅角相加。
所以有:
0.3.2. 性质
- (omega_n^j=omega_{n imes k}^{j imes k})。这就是 (e) 的指数分子分母同时乘上 (k),所以相等。
- (omega_n^j=-omega_n^{j+frac{n}{2}})。容易发现就是辐角加上 (pi)。
- (omega_n^n=1)。显然 (e^{2pi i}=1 imes (cos 2pi +isin 2pi)=1)。
1. 正文
1.1. (mathtt{FFT}) 可以干什么
求两个多项式 (f,g) 相乘:((a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}) imes (b_0+b_1x+b_2x^2+...+b_{m-1}x^{m-1}))。
显然我们需要计算 (x) 的 (0) 到 (n+m-2) 次方项的系数。
虽然我们得到和最终要求的都是系数多项式,可我们发现点值多项式合并只需要 (y) 相乘,整体复杂度是 (mathcal O(n)) 的。
如果我们能快速地转换系数多项式与点值多项式,就能快速求解原问题。
朴素是 (mathcal O(n^2)) 的,而 (mathtt{FFT}) 可以优化到 (mathcal O(nlog n))。
1.2. 系数多项式 ( ightarrow) 点值多项式
将系数多项式按下标的奇偶分成两个函数(认为 (n) 是 (2) 的正整数幂,如果不够可以补 (0) 系数):
那么有:
傅里叶说:我们选择 (omega_n^i) 为点值多项式代入的 (x_i)。
那么对于 (i<frac{n}{2}) 就有:
同时 (f_1,f_2) 又是新的 (f),这就是一个迭代的过程。
1.3. 点值多项式 ( ightarrow) 系数多项式
得到的 (y_i=sum_{j=0}^{n-1}a_j(omega_n^i)^j)。
傅里叶说:我们选择 (omega_n^{-i}) 为点值多项式代入的 (x_i),(y_i) 为新的系数,再做一次。
后面那一坨是等比数列,如果公比不为 (1) 时易得为 (0),当公比为 (1) 即 (i=j) 时为 (n)。
所以有:
我们就转回去了。
1.4. 代码
说了这么多,终于来点实在的了。

由于我们递归地划分,原多项式和末多项式相同下标有奇怪的联系:二进制是相反的。
为了模拟递归,我们可以先求出末多项式再倒回来算。具体算法和解析戳这。
具体看代码吧。
#include <cstdio>
#define rep(i,_l,_r) for(register signed i=(_l),_end=(_r);i<=_end;++i)
#define fep(i,_l,_r) for(register signed i=(_l),_end=(_r);i>=_end;--i)
#define erep(i,u) for(signed i=head[u],v=to[i];i;i=nxt[i],v=to[i])
#define efep(i,u) for(signed i=Head[u],v=to[i];i;i=nxt[i],v=to[i])
#define print(x,y) write(x),putchar(y)
template <class T> inline T read(const T sample) {
T x=0; int f=1; char s;
while((s=getchar())>'9'||s<'0') if(s=='-') f=-1;
while(s>='0'&&s<='9') x=(x<<1)+(x<<3)+(s^48),s=getchar();
return x*f;
}
template <class T> inline void write(const T x) {
if(x<0) return (void) (putchar('-'),write(-x));
if(x>9) write(x/10);
putchar(x%10^48);
}
template <class T> inline T Max(const T x,const T y) {if(x>y) return x; return y;}
template <class T> inline T Min(const T x,const T y) {if(x<y) return x; return y;}
template <class T> inline T fab(const T x) {return x>0?x:-x;}
template <class T> inline T gcd(const T x,const T y) {return y?gcd(y,x%y):x;}
template <class T> inline T lcm(const T x,const T y) {return x/gcd(x,y)*y;}
template <class T> inline T Swap(T &x,T &y) {x^=y^=x^=y;}
#include <cmath>
#include <iostream>
using namespace std;
const int maxn=3e6+5;
const double Pi=acos(-1.0);
int n,m,lim=1,bit,rev[maxn];
struct cp {
double x,y;
cp operator + (const cp t) {
return (cp) {x+t.x,y+t.y};
}
cp operator - (const cp t) {
return (cp) {x-t.x,y-t.y};
}
cp operator * (const cp t) {
return (cp) {x*t.x-y*t.y,y*t.x+x*t.y};
}
void Give(const double X,const double Y) {
x=X,y=Y;
}
} a[maxn],b[maxn],wn,w,tmp;
void init() {
while(lim<=n+m) lim<<=1,++bit;
// n+m 是最高项指数,由于 n 是 [0,n-1],所以这里是 <=
rep(i,0,lim-1) rev[i]=(rev[i>>1]>>1)|((i&1)<<bit-1);
}
void FFT(cp *t,int op) {
rep(i,0,lim-1) if(i<rev[i]) swap(t[i],t[rev[i]]);
// 求末多项式,要求 i<rev[i] 是为避免重复交换
for(int mid=1;mid<lim;mid<<=1) {
// mid 是枚举所在递归层 x 对应 f 的长度,其中递归层 x 已经被计算,现在要计算 x 上一层(即从 f_1,f_2 贡献到 f)
wn.Give(cos(Pi/mid),sin(Pi/mid)*op);
// wn 是 w_{mid*2},就是 x 上一层的单位复根
// *op 是求 wn 的共轭复数,即 wn^{-1}(转回去需要),显然把这两个用欧拉公式可以得到两个互为相反数的辐角,所以横坐标不变,纵坐标相反
for(int i=0;i<lim;i+=(mid<<1)) {
// i 是找 x 的上一层的每一段的开头
w.Give(1,0);
// w 用来模拟单位复根的几次幂,初始化幅角为 0(cos(0)=1,sin(0)=0)
for(int j=0;j<mid;++j,w=w*wn) {
// x 这一层的每一段用 j 来遍历
/*
0 1 2 3 4 5 6 7
0 2 4 6|1 3 5 7 y
0 4|2 6|1 5|3 7 x
0|4|2|6|1|5|3|7
这是一个递归
y 层的 0,4 根据公式由 x 层的 0,2 贡献
*/
tmp=w*t[i+j+mid];
t[i+j+mid]=t[i+j]-tmp,t[i+j]=t[i+j]+tmp;
}
}
}
}
int main() {
n=read(9),m=read(9);
rep(i,0,n) scanf("%lf",&a[i].x);
rep(i,0,m) scanf("%lf",&b[i].x);
init();
FFT(a,1),FFT(b,1);
rep(i,0,lim) a[i]=a[i]*b[i];
FFT(a,-1);
rep(i,0,n+m) printf("%d ",(int)(a[i].x/lim+0.5));
return 0;
}
2. 拓展
有 拆系数 (mathtt{FFT}),欢迎资瓷!