前言
李超线段树是线段树的一个变种,支持在平面直角坐标系中动态插入线段,查询一条竖线与所有线段的交点纵坐标的最大值或最小值。
引入
下面以 【HEOI2013】Segment 为例讲解李超线段树。
题目大意:
要求在平面直角坐标系下维护两个操作:
- 在平面上加入一条线段。记第 \(i\) 条被插入的线段的标号为 \(i\)。
- 给定一个数 \(k\),询问与直线 \(l:x=k\) 相交的线段中,交点纵坐标最大的线段的编号。
对于线段树上每一个结点,维护一个区间最优线段。当一条线段满足以下条件时,它才能成为最优线段:
- 该线段的定义域覆盖整个区间。
- 该线段在区间中点处的值最大。
令区间 \([L,R]\) 当前最优线段为 \(l'\) ,考虑如何在区间 \([L,R]\) 中插入线段 \(l\):
- 若当前区间没有最优线段,或者线段 \(l′\) 被线段 \(l\) 完全覆盖(对于这道题,指线段 \(l′\) 完全在插入线段下),那么线段 \(l\) 直接成为当前区间的最优线段。
- 若线段 \(l\) 被线段 \(l′\) 完全覆盖 一转攻势,那么线段 \(l\) 就没用了,不用再向下递归。
- 否则,线段 \(l\) 与线段 \(l'\) 相交。令区间中点为 \(mid\) ,比较线段 \(l\) 和线段 \(l'\) 在中点 \(mid\) 处的纵坐标大小,更新当前区间最优线段。
对于第三种情况,虽然线段 \(l'\) 在当前区间中不再是最优线段了,但是它依然可能成为子区间的最优线段,代码实现中是交换线段 \(l\) 和线段 \(l'\),用线段 \(l'\) 更新子区间信息。
考虑如何更新子结点信息。令用来更新子区间信息的线段为 \(l''\)(因为上面更新过最优线段,所以线段 \(l''\) 一定是在 \(mid\) 处纵坐标较小的线段),对交点位置分类讨论:
-
若交点在 \(mid\) 左侧,如图:
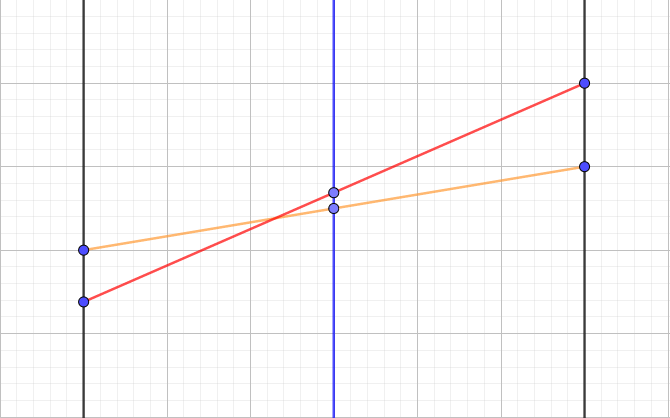
红色线段为当前最优线段,橙色线段为线段 \(l''\),此时线段 \(l''\) 只有可能在左子区间中成为最优线段,所以只需在线段树上更新左儿子的信息。
-
若交点在 \(mid\) 右侧,同理,更新右儿子信息。
-
若交点在 \(mid\) 处,若线段 \(l''\) 在 \(L\) 处的纵坐标较大,更新左儿子,否则更新右儿子。
查询时在线段树上二分找到这个位置,比较途径的所有区间的最优线段在这个位置时的纵坐标,取最大值即可。这其实是标记永久化的思想。
代码:
用结构体封装一条线段:
struct line
{
double k,b;// 斜率
int id; // 部分题需要记录线段编号
line(double k=0,double b=0,int id=0):k(k),b(b),id(id){}
inline double calcu(int pos) // 计算线段在pos位置的纵坐标
{
return k*pos+b;
}
inline double cross(const line &T) // 求两条线段的交点横坐标
{
return (T.b-b)/(k-T.k);
}
};
线段树结点:
struct node
{
int l,r; // 区间左右端点
line L; // 最优线段
bool flag; // 记录区间内是否有最优线段
node(int l,int r,line L,bool flag):l(l),r(r),L(L),flag(flag){}
node(){}
}tree[maxn<<2];
#define ls (p<<1) // 左儿子
#define rs (p<<1|1) // 右儿子
建树:
inline void build(int p,int l,int r)
{
tree[p]=node(l,r,line(),false);
// 新建一个没有最优线段的结点
if(l==r) return;
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
最重要的 modify 操作:
这里并没有计算出交点横坐标,因为交点位置可以通过比较线段在端点处的纵坐标得出:
最优线段在 \(mid\) 处的取值一定较大,如果插入线段在左端点的取值较大,那么交点在左子区间,否则在右子区间。
这样计算同时也避免了多讨论交点在 \(mid\) 处的情况。
inline void modify(int p,int L,int R,line ln)
{
int l=tree[p].l,r=tree[p].r;
if(L<=l&&r<=R) // 如果插入线段的定义域覆盖整个区间
{
double lp=tree[p].L.calcu(l),rp=tree[p].L.calcu(r);
double lq=ln.calcu(l),rq=ln.calcu(r);
// 计算两条线段在区间端点的纵坐标
if(!tree[p].flag) tree[p].L=ln,tree[p].flag=true;
else if(lq-lp>eps&&rq-rp>eps) tree[p].L=ln;
// 没有最优线段或者完全覆盖
else if(lq-lp>eps||rq-rp>eps) // 相交
{
int mid=(l+r)>>1;
if(ln.calcu(mid)-tree[p].L.calcu(mid)>eps) swap(tree[p].L,ln);
if(ln.calcu(l)>tree[p].L.calcu(l))
modify(ls,L,R,ln);
else modify(rs,L,R,ln);
}
}
else // 若未覆盖整个区间,检查子区间
{
int mid=(l+r)>>1;
if(L<=mid) modify(ls,L,R,ln);
if(R>mid) modify(rs,L,R,ln);
}
}
查询:
typedef pair<double,int> pii;
inline pii query(int p,int pos) // 本题还要返回线段编号
{
int l=tree[p].l,r=tree[p].r;
double ans=tree[p].L.calcu(pos);
int id=tree[p].L.id;
if(l==r) return make_pair(ans,id);
int mid=(l+r)>>1;
if(pos<=mid)
{
pii lq=query(ls,pos);
if(lq.first>ans||(fabs(lq.first-ans)<eps&&lq.second<id))
ans=lq.first,id=lq.second;
}
else
{
pii rq=query(rs,pos);
if(rq.first>ans||(fabs(rq.first-ans)<eps&&rq.second<id))
ans=rq.first,id=rq.second;
}
return make_pair(ans,id);
}
复杂度分析
每次修改将区间分成 \(\log n\) 个子区间,每个子区间的最优线段最多下放 \(\log n\) 层,所以修改复杂度为 \(O(\log n)\)。
每次查询经过 \(\log n\) 个结点,复杂度 \(O(\log n)\)。
