本篇文章,灵感来自于一步一步理解线段树③,但是又与其的代码讲述实现有些不同。
目录:
一、线段树的定义
二、线段树的基本操作
三、实战演练
四、代码展示
一、线段树的基本概念:
1.定义
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。线段树至少支持下列操作:Insert(t,x):将包含在区间 int 的元素 x 插入到树t中;Delete(t,x):从线段树 t 中删除元素 x;Search(t,x):返回一个指向树 t 中元素 x 的指针。
但是百科的定义往往让人望而却步,此处我用一种网上的较为“简洁”的定义:
线段树是一种针对于数据规模较大的区间查询和操作的一种数据结构(完全二叉树②),基于线段树的二叉树结构,对它的每次查询或者改变的操作,复杂度可视为O(logn)。并且线段树的每一个节点可以用来表示一个固定的区间。由于线段树是完全二叉树,所以线段树的叶子结点所表示的区间长度是最短的,可以视为是线段树的“底层”(按树的定义来说应该是最高层)。
2.基本思想:递归、二分
以二分的方式查询、修改,以递归的方式建树、查询回溯、修改回溯。
3.数据结构类型:树(完全二叉树)
完全二叉树定义:
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。一棵二叉树至多只有最下面的一层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,而在最后一层上,右边的若干结点缺失的二叉树,则此二叉树成为完全二叉树。
4.性质:
1’对于当前的节点root,其左孩子的下标为root*2,右孩子的下标root*2+1
2’左孩子管辖的区间范围为【L,MID】,右孩子管辖的区间范围为【MID+1,R】
3’有着完全二叉树的性质。
二、线段树的基本操作
下面我们以一道线段树的经典模板题引入【区间修改询问求和问题】,来源:洛谷②;
题目大意:已知一个数列,你需要多次操作,每次操作有两种,一个是将某个区间内的所有数加上X,一个是询问某个区间内所有数的和;对于100%的数据:N<=100000,M<=100000
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输入样例#1:5 5 //n个数和m次操作
1 5 4 2 3 //已知数列
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
输出样例#1:11
8
20
解法1:每次模拟,显然时间是会爆炸的,O(100000*100000)>1s
解法2:树状数组,但是由于是动态查询修改的,导致对于树状数组的维护需要浪费掉非常多的时间
解法3:线段树!
我们可以用线段树来解决这个问题:预处理耗时O(n),查询、更新操作O(logn),需要额外的空间O(n)。
由于线段树的父节点区间是平均分割到左右子树,因此线段树是完全二叉树,对于包含n个叶子节点的完全二叉树,它一定有n-1个非叶节点,总共2n-1个节点,因此存储线段是需要的空间复杂度是O(n)。③
叶子节点是原始组数a中的元素
非叶子节点代表它的所有子孙叶子节点所在区间之和

我们如图创建好线段树(这个是初始化版的),从而进行查询!
1.创建线段树(万事开头难,这关过了后面相对也就简单了)
对于线段树我们可以选择和普通二叉树一样的链式结构。
由于线段树是完全二叉树,我们也可以用结构体定义的数组来存储,下面的讨论及代码都是运用结构体的数组来存储线段树,节点结构如下(注意到用数组存储时,有效空间为2n-1,实际空间确不止这么多,比如上面的线段树中我们有总共4个点的空间虽然是0的初始值,但是确实占据了一定的数组空间,实际上我们要的空间是满二叉树所需要的总空间,所以经常做线段树的时候都会听到人家说:线段树开个4倍空间稳稳过就是这个意思 )。
定义当前线段树代码:
struct fkt{ int left; //记录左区间的位置 int right; //记录右区间的位置 int tot; //记录当前区间的和 }tree[MAXN]; //定义一棵线段树 void build(int lef,int rig,int root){ //从lef到rig的距离以root为根建树(前提是要求rig-lef+1能够构成一个完全二叉树)
tree[root].left=lef; //记录左区间的位置 tree[root].right=rig; //记录右区间的位置 if(lef==rig){tree[root].tot=a[lef];} //到达底端,我们直接把数组中存下的数复制给线段树 else{ //否则递归的去构造左右子树 int mid=(lef+rig)>>1; build(lef,mid,root<<1); build(mid+1,rig,root<<1|1); //并且根据左右子树节点的值来更新我当前的根节点的值 tree[root].tot=tree[root<<1].tot+tree[root<<1|1].tot; } }
2.查询线段树的各个区间
构建好线段树后,我们就得到了上图的那种线段树,但是要如何进行查询呢?
我们前面有提到,线段树的基本思想是递归和二分,所以我们能不能用递归、二分的思想查询呢?
答案是可以的!
假设我们要查找区间[3,7]的值我们怎么做呢?如图:
我们先将所要查询的区间与当前区间进行比较,显然[3,7]是在[1,8]的里面的,所以我们就去根节点的两个孩子节点里找自己所需要的求值

然后我们将分开后的区间继续比较。
显然,[3,4]在[1,4]内,所以直接继续去根节点的两个孩子节点里找自己所需要的求值
显然,[5,7]在[5,8]内,所以直接继续去根节点的两个孩子节点里找自己所需要的求值

同理,不谈。
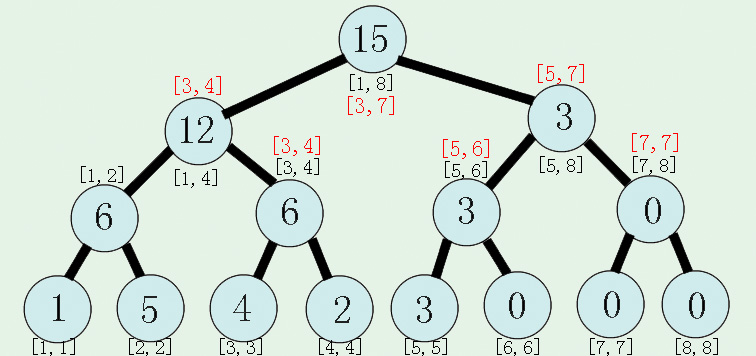
最后找到根节点的时候因为这个时候是有值的,所以进行返回操作,将值传回去给自己的父节点。
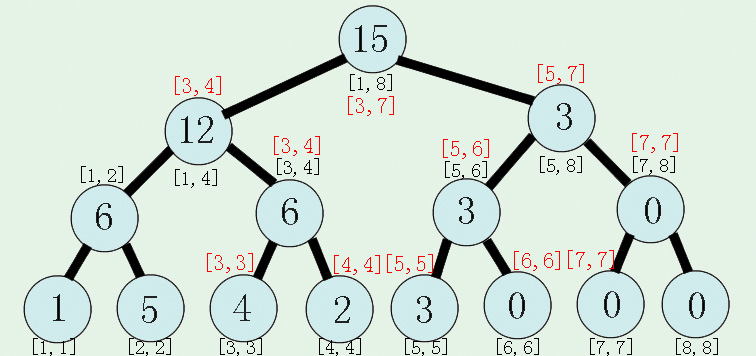
最后输出9即为[3,7]查询的正解
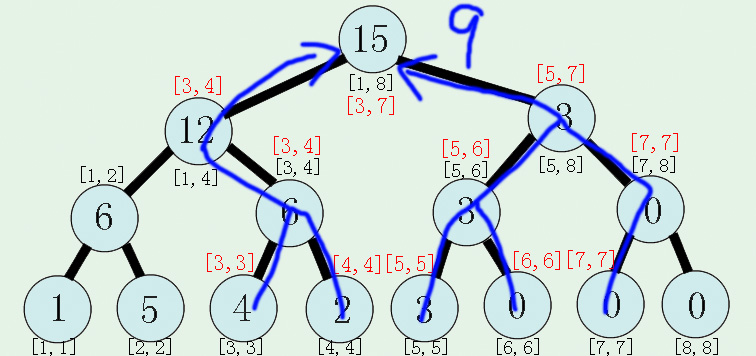
那我们看懂图解了,代码实现就简单多了!
显然,我们在做的时候是有一些多余的操作的,每一次都要访问到底才返回。这样线段树的优势又在哪里呢?
我们发现: 对于[3,4]的这个区间,我们已经预处理过它的值了,所以可以不用继续访问,直接返回。
对于[5,6]的区间,同样是因为全部相等,所以直接返回。
对于[7,8]的区间,因为[7,7]并不能完全覆盖[7,8],换个意思讲就是[7,8]并不是[7,7]的子区间。这个时候我们只能继续递归到正好满足当前查询区间为目标区间的子区间就可以返回了
实际上这样的工作效率就会非常的高。
查询的思想是选出一些区间,使他们相连后恰好涵盖整个查询区间,因此线段树适合解决“相邻的区间的信息可以被合并成两个区间的并区间的信息”的问题。
线段树查询代码实现:
/* [nl,nr]表示此次所查询的区间 root表示我当前所访问到的节点编号 ∵我前面曾经存储过树的左右孩子 所以我当前的区间就可以直接用[tree[root].left,tree[root].right]表示 */ int query(int nl,int nr,int root){ if(tree[root].left>nr||tree[root].right<nl) return 0; //如果二者没有交集则返回一个极小的值 if(tree[root].left>=nl&&tree[root].right<=nr) return tree[root].tot; //如果这个当前区间本身就是属于我要求的那个区间,那么我就不继续递归了,直接回溯 //实际上图解中是仍旧递归到最后的,所以不免会多一些操作,耗费时间 //像这样就比较简便。 return query(nl,nr,root<<1)+query(nl,nr,root<<1|1); }
3.更新线段树的节点
显然,如果更新单节点的话我们完全可以直接用树状数组④解决,
而题目要求的是区间性的修改和查询访问,所以树状数组的二进制应用是行不通的。
(我自认为)线段树最高明的地方就在于懒惰标记(lazy_tag)
因为有了懒惰标记(lazy_tag)才使得线段树变得高效,方便。
一般来说,我们对于区间内的所有元素的修改,显然如果逐个递归回溯修改,把每一次的区间更新完,是极其耗费时间的(显然不可能是O(logn)),线段树引入懒惰标记就可以保证“只拿这次对我有用的,这次对我有用的一次性拿光,暂时没用的先不管他,可以先存着”。
在本文中,我们以add表示lazy_tag,同时我们需要一个维护线段树的函数update、一个向下传递懒惰标记(lazy_tag)的函数pushdown、一个向上传递值的函数pushup来更新。
懒惰标记的含义即对于我当前的[tree[root].left,tree[root].right],暂时有lazy_tag的数还没加上去,我们不急着加,等到要用或者访问查询的时候才用它,这样可以节省了很多不必要的操作,这就是线段树能做到O(nlogn)的一个重要原因!。
代码实现如下:
//从建树开始重新说起 void build(int lef,int rig,int root){ tree[root].left=lef; tree[root].right=rig; tree[root].add=0; //懒惰标记lazy_tag if(lef==rig){tree[root].tot=a[lef];} else{ int mid=(lef+rig)>>1; build(lef,mid,root<<1); build(mid+1,rig,root<<1|1); tree[root].tot=tree[root<<1].tot+tree[root<<1|1].tot; //要记得把线段树先初始化一下 } }
//向下传递懒惰标记(lazy_tag)(说明自己现在需要当前的根加上懒惰标记了,而我不想浪费时间地去递归把剩下的给一次性更新完,所以我们考虑直接传递懒惰标记,不更新左右孩子,除非我需要。) void pushdown(int root){ if(tree[root].add){ tree[root<<1].add+=tree[root].add; tree[root<<1|1].add+=tree[root].add; //当前区间加上了懒惰标记的值实际上加的值是lazy_tag*区间长度 //画一下图就可以知道了 tree[root<<1].tot+=tree[root].add*(tree[root<<1].right-tree[root<<1].left+1); tree[root<<1|1].tot+=tree[root].add*(tree[root<<1|1].right-tree[root<<1|1].left+1); tree[root].add=0; }
}
//向上推传递值,说白了就是刷新一下自身的值(保证下面的值改变的时候自己也会改变) void pushup(int root){ tree[root].tot=tree[root<<1].tot+tree[root<<1|1].tot; }
/*区间更新,意思: 当前的更新区间为[tree[root].left,tree[root].right] 目标的更新区间为[nl,nr] 显然如果没交集就不管他。 如果二者区间有交集我们再详细处理 如果当前查找的区间是我们目标区间的其中一个子区间,自然直接返回即可。 (当初我这里也是搞得乱乱的,推荐大家可以做图一下,画个图一下就看出来了。) */ void update(int nl,int nr,int root,int c){ if(tree[root].left>nr||tree[root].right<nl) return; if(tree[root].left>=nl&&tree[root].right<=nr){ tree[root].add+=c; tree[root].tot+=c*(tree[root].right-tree[root].left+1); return; } pushdown(root); int mid=(tree[root].left+tree[root].right)>>1; if(nl<=mid) update(nl,nr,root<<1,c); if(mid+1<=nr) update(nl,nr,root<<1|1,c);
pushup(root); }
//查询工作,在[nl,nr]的区间内查找,当前查找[tree[root].left,tree[root].right]区间 int query(int nl,int nr,int root){ if(tree[root].left>nr||tree[root].right<nl) return 0; //返回一个极小的值 if(tree[root].left>=nl&&tree[root].right<=nr) return tree[root].tot; pushdown(root); //向下传递才能计算求和。 return query(nl,nr,root<<1)+query(nl,nr,root<<1|1); //返回所计算的求和 }
实际上这题就完成了!而且我们也学会了线段树的一些基本操作!
三、实战演练
1.线段树模板1【实现区间加法并且动态查询】
链接: https://www.luogu.org/problem/show?pid=3372
2.线段树模板2【实现区间加法与乘法并且动态查询】
链接: https://www.luogu.org/problem/show?pid=3373
3. [JSOI2008]最大数
链接: https://www.luogu.org/problem/show?pid=1198
本人代码在底部,可借鉴,请勿抄袭!
四、代码展示
1.CODE:
1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 LL op,n,m,x,y,k,a[300005],low_bit,tempt; 5 struct fkt{ 6 LL left; 7 LL right; 8 LL tot; 9 LL add; 10 }tree[300005]; 11 namespace qaq{ 12 LL change(LL test){LL ans=0;while(test){test>>=1;ans++;}test=1;while(ans--)test*=2;return test;} 13 void build(LL lef,LL rig,LL root){ 14 tree[root].left=lef; 15 tree[root].right=rig; 16 tree[root].add=0; 17 if(lef==rig){tree[root].tot=a[lef];} 18 else{ 19 LL mid=(lef+rig)>>1; 20 build(lef,mid,root<<1); 21 build(mid+1,rig,root<<1|1); 22 tree[root].tot=tree[root<<1].tot+tree[root<<1|1].tot; 23 } 24 } 25 void pushdown(LL root){ 26 if(tree[root].add){ 27 tree[root<<1].add+=tree[root].add; 28 tree[root<<1|1].add+=tree[root].add; 29 tree[root<<1].tot+=tree[root].add*(tree[root<<1].right-tree[root<<1].left+1); 30 tree[root<<1|1].tot+=tree[root].add*(tree[root<<1|1].right-tree[root<<1|1].left+1); 31 tree[root].add=0; 32 } 33 } 34 void pushup(LL root){ 35 tree[root].tot=tree[root<<1].tot+tree[root<<1|1].tot; 36 } 37 void update(LL nl,LL nr,LL root,LL c){ 38 if(tree[root].left>nr||tree[root].right<nl) return; 39 if(tree[root].left>=nl&&tree[root].right<=nr){ 40 tree[root].add+=c; 41 tree[root].tot+=c*(tree[root].right-tree[root].left+1); 42 return; 43 } 44 pushdown(root); 45 LL mid=(tree[root].left+tree[root].right)>>1; 46 if(nl<=mid) update(nl,nr,root<<1,c); 47 if(mid+1<=nr) update(nl,nr,root<<1|1,c); 48 pushup(root); 49 } 50 LL query(LL nl,LL nr,LL root){ 51 if(tree[root].left>nr||tree[root].right<nl) return 0; 52 if(tree[root].left>=nl&&tree[root].right<=nr) return tree[root].tot; 53 pushdown(root); 54 return query(nl,nr,root<<1)+query(nl,nr,root<<1|1); 55 } 56 57 int main(){ 58 scanf("%lld%lld",&n,&m); 59 for(LL i=1;i<=n;i++) scanf("%lld",&a[i]); 60 tempt=change(n); 61 build(1,tempt,1); 62 while(m--){ 63 scanf("%lld",&op); 64 if(op==1){ 65 scanf("%lld%lld%lld",&x,&y,&k); 66 update(x,y,1,k); 67 } 68 else{ 69 scanf("%lld%lld",&x,&y); 70 printf("%lld ",query(x,y,1)); 71 } 72 } 73 return 0; 74 } 75 } 76 int main(){ 77 qaq::main(); 78 return 0; 79 }
2.CODE:
1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 LL op,n,m,x,y,k,a[300005],low_bit,tempt,p; 5 struct fkt{ 6 LL left; 7 LL right; 8 LL tot; 9 LL multi; 10 LL add; 11 }tree[300005]; 12 namespace qaq{ 13 LL change(LL test){LL ans=0;while(test){test>>=1;ans++;}test=1;while(ans--)test*=2;return test;} 14 void build(LL lef,LL rig,LL root){ 15 tree[root].left=lef; 16 tree[root].right=rig; 17 if(lef==rig){tree[root].tot=a[lef]%p;} 18 else{ 19 LL mid=(lef+rig)>>1; 20 build(lef,mid,root<<1); 21 build(mid+1,rig,root<<1|1); 22 tree[root].tot=tree[root<<1].tot+tree[root<<1|1].tot; 23 tree[root].tot%=p; 24 } 25 } 26 void pushdown(LL root){ 27 if(tree[root].multi!=1){ 28 tree[root<<1].add*=tree[root].multi; 29 tree[root<<1].add%=p; 30 tree[root<<1|1].add*=tree[root].multi; 31 tree[root<<1|1].add%=p; 32 tree[root<<1].multi*=tree[root].multi; 33 tree[root<<1].multi%=p; 34 tree[root<<1|1].multi*=tree[root].multi; 35 tree[root<<1|1].multi%=p; 36 tree[root<<1].tot*=tree[root].multi; 37 tree[root<<1].tot%=p; 38 tree[root<<1|1].tot*=tree[root].multi; 39 tree[root<<1|1].tot%=p; 40 tree[root].multi=1; 41 } 42 if(tree[root].add){ 43 tree[root<<1].add+=tree[root].add; 44 tree[root<<1].add%=p; 45 tree[root<<1|1].add+=tree[root].add; 46 tree[root<<1|1].add%=p; 47 tree[root<<1].tot+=tree[root].add*(tree[root<<1].right-tree[root<<1].left+1); 48 tree[root<<1].tot%=p; 49 tree[root<<1|1].tot+=tree[root].add*(tree[root<<1|1].right-tree[root<<1|1].left+1); 50 tree[root<<1|1].tot%=p; 51 tree[root].add=0; 52 } 53 } 54 void pushup(LL root){ 55 tree[root].tot=tree[root<<1].tot+tree[root<<1|1].tot; 56 } 57 void update(LL nl,LL nr,LL root,LL c,bool cc){ 58 if(tree[root].left>nr||tree[root].right<nl) return; 59 if(tree[root].left>=nl&&tree[root].right<=nr){ 60 if(cc==0){ 61 tree[root].add+=c; 62 tree[root].add%=p; 63 tree[root].tot+=c*(tree[root].right-tree[root].left+1); 64 tree[root].tot%=p; 65 } 66 else{ 67 tree[root].multi*=c; 68 tree[root].multi%=p; 69 tree[root].add*=c; 70 tree[root].add%=p; 71 tree[root].tot*=c; 72 tree[root].tot%=p; 73 } 74 return; 75 } 76 LL mid=(tree[root].left+tree[root].right)>>1; 77 pushdown(root); 78 if(nl<=mid) update(nl,nr,root<<1,c,cc); 79 if(mid+1<=nr) update(nl,nr,root<<1|1,c,cc); 80 pushup(root); 81 } 82 LL query(LL nl,LL nr,LL root){ 83 if(tree[root].left>nr||tree[root].right<nl) return 0; 84 if(tree[root].left>=nl&&tree[root].right<=nr) return tree[root].tot; 85 pushdown(root); 86 LL x=query(nl,nr,root<<1)%p; 87 LL y=query(nl,nr,root<<1|1)%p; 88 pushup(root); 89 return (x+y)%p; 90 } 91 int main(){ 92 scanf("%lld%lld%lld",&n,&m,&p); 93 for(LL i=1;i<=300000;i++){ 94 tree[i].multi=1; 95 tree[i].add=0; 96 } 97 for(LL i=1;i<=n;i++){ 98 scanf("%lld",&a[i]); 99 a[i]%=p; 100 } 101 tempt=change(n); 102 build(1,tempt,1); 103 while(m--){ 104 scanf("%lld",&op); 105 if(op==1){//乘法 106 scanf("%lld%lld%lld",&x,&y,&k); 107 update(x,y,1,k,1); 108 } 109 else if(op==2){//加法 110 scanf("%lld%lld%lld",&x,&y,&k); 111 update(x,y,1,k,0); 112 } 113 else{ 114 scanf("%lld%lld",&x,&y); 115 printf("%lld ",query(x,y,1)%p); 116 } 117 } 118 return 0; 119 } 120 } 121 int main(){ 122 qaq::main(); 123 return 0; 124 }
3.CODE:
1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 LL m,p,t=0,len=0,n; 5 char op; 6 struct fkt{ 7 LL left; 8 LL right; 9 LL numb; 10 }tree[2400000]; 11 namespace qaq{ 12 LL query(LL l,LL r,LL root,LL ql,LL qr){ 13 LL ans=-999999999; 14 if(ql<=l&&qr>=r) return tree[root].numb; 15 LL mid=(l+r)>>1; 16 if(ql<=mid) ans=max(ans,query(l,mid,root<<1,ql,qr)); 17 if(mid+1<=qr) ans=max(ans,query(mid+1,r,root<<1|1,ql,qr)); 18 return ans; 19 } 20 21 void update(LL l,LL r,LL root,LL place,LL x){ 22 if(l==r){tree[root].numb=x;return;} 23 LL mid=(l+r)>>1; 24 if(place<=mid) update(l,mid,root<<1,place,x); 25 else update(mid+1,r,root<<1|1,place,x); 26 tree[root].numb=max(tree[root<<1].numb,tree[root<<1|1].numb); 27 } 28 29 int main(){ 30 cin>>m>>p; 31 for(LL i=1;i<=m;i++)tree[i].numb=-999999999; 32 while(m--){ 33 cin>>op>>n;; 34 if(op=='A'){ 35 len++; 36 n=(n+t)%p; 37 update(1,262144,1,len,n); 38 } 39 else{ 40 t=query(1,262144,1,len-n+1,len); 41 printf("%lld ",t); 42 } 43 } 44 return 0; 45 } 46 } 47 int main(){ 48 qaq::main(); 49 return 0; 50 }
欢迎纠错。等待补充......
参考文献、资料或解释:
①:【线段树】
https://baike.baidu.com/item/%E7%BA%BF%E6%AE%B5%E6%A0%91/10983506?fr=aladdin#ref_[2]_670683
②:【线段树模板:区间修改询问求和问题】 https://www.luogu.org/problem/show?pid=3372
③:【一步一步理解线段树】http://www.cnblogs.com/TenosDoIt/p/3453089.html
④:【树状数组】可参考该博客 http://www.cnblogs.com/hsd-/p/6139376.html