#1143 : 骨牌覆盖问题·一
描述
骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题:
我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢?
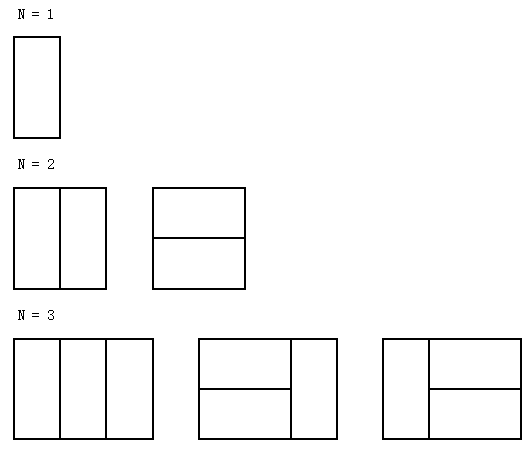
举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式:
我们考虑在已经放置了部分骨牌(灰色)的情况下,下一步可以如何放置新的骨牌(蓝色):
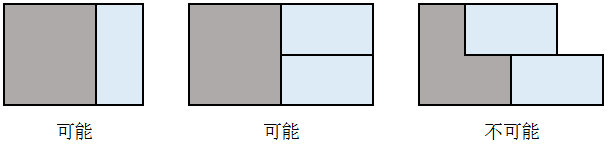
最右边的一种情况是不可能发生的,否则会始终多一个格子没有办法放置骨牌。或者说灰色部分的格子数为奇数,不可能通过1x2个骨牌放置出来。
那么通过对上面的观察,我们可以发现:
在任何一个放置方案最后,一定满足前面两种情况。而灰色的部分又正好对应了长度为N-1和N-2时的放置方案。由此,我们可以得到递推公式:
f[n] = f[n-1] + f[n-2];
这个公式是不是看上去很眼熟?没错,这正是我们的费波拉契数列。
f[0]=1,f[1]=1,f[2]=2,...
提示:如何快速计算结果
当N很小的时候,我们直接通过递推公式便可以计算。当N很大的时候,只要我们的电脑足够好,我们仍然可以直接通过递推公式来计算。
但是我们学算法的,总是这样直接枚举不是显得很Low么,所以我们要用一个好的算法来加速(装X)。
事实上,对于这种线性递推式,我们可以用矩阵乘法来求第n项。对于本题Fibonacci数列,我们希望找到一个2x2的矩阵M,使得(a, b) x M = (b, a+b),其中(a, b)和(b, a+b)都是1x2的矩阵。
显然,只需要取M = [0, 1; 1, 1]就可以了:
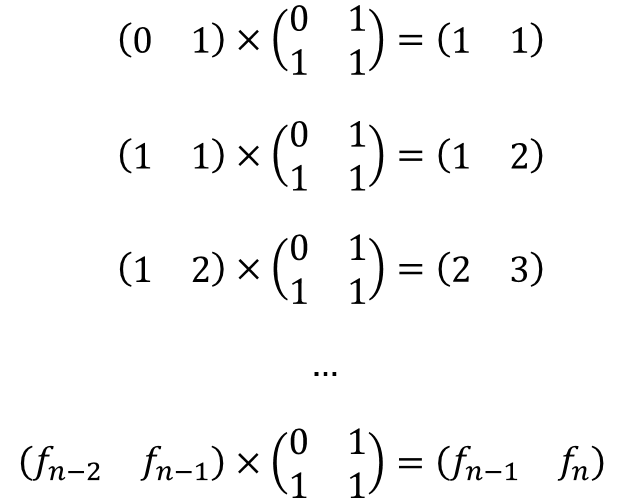
进一步得到:

那么接下来的问题是,能不能快速的计算出M^n?我们先来分析一下幂运算。由于乘法是满足结合律的,所以我们有:
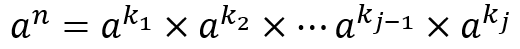
不妨将k[1]..k[j]划分的更好一点?
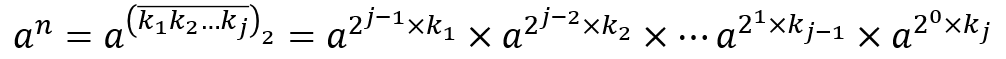
其中(k[1],k[2]...k[j])2表示将n表示成二进制数后每一位的数字。上面这个公式同时满足这样一个性质:
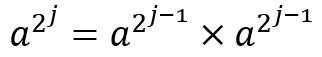
结合这两者我们可以得到一个算法:
1. 先计算出所有的{a^1, a^2, a^4 ... a^(2^j)},因为该数列满足递推公式,时间复杂度为O(logN)
2. 将指数n二进制化,再利用公式将对应的a^j相乘计算出a^n,时间复杂度仍然为O(logN)
则总的时间复杂度为O(logN)
这种算法因为能够在很短时间内求出幂,我们称之为“快速幂”算法。
分析:构造矩阵,然后矩阵快速幂。
递归写法:

#include<cstdio> #include<cstring> #include<algorithm> #define mod 19999997 using namespace std; struct matrix{ long long A[3][3]; }; matrix E; matrix mul(matrix x,matrix y) { matrix ans; for(int i=1;i<3;i++) for(int j=1;j<3;j++) { long long temp=0; for(int k=1;k<3;k++) temp+=x.A[i][k]*y.A[k][j]; ans.A[i][j]=temp%mod; } return ans; } matrix powmul(matrix x,int k) { if(k==1) return x; matrix y=powmul(x,k/2); y=mul(y,y); if(k%2) y=mul(y,x); return y; } int main() { int N; E.A[1][1]=E.A[1][2]=E.A[2][1]=1; E.A[2][2]=0; scanf("%d",&N); if(N<3) printf("%d ",N); else { matrix ans=powmul(E,N-2); printf("%lld ",(2*ans.A[1][1]+ans.A[1][2])%mod); } return 0; }
非递归写法:

#include<cstdio> #include<cstring> #include<algorithm> #define mod 19999997 using namespace std; struct matrix{ long long A[3][3]; }; matrix E; matrix mul(matrix x,matrix y) { matrix ans; for(int i=1;i<3;i++) for(int j=1;j<3;j++) { long long temp=0; for(int k=1;k<3;k++) temp+=x.A[i][k]*y.A[k][j]; ans.A[i][j]=temp%mod; } return ans; } matrix powmul(matrix x,int k) { matrix ans;//注意ans开始时是二阶单位矩阵,相当与实数时的1 ans.A[1][1]=ans.A[2][2]=1; ans.A[1][2]=ans.A[2][1]=0; while(k>0) { if(k&1) ans=mul(ans,x); k=k>>1; x=mul(x,x); } return ans; } int main() { int N; E.A[1][1]=E.A[1][2]=E.A[2][1]=1; E.A[2][2]=0; scanf("%d",&N); if(N<3) printf("%d ",N); else { matrix ans=powmul(E,N-2); printf("%lld ",(2*ans.A[1][1]+ans.A[1][2])%mod); } return 0; }
