矩阵树定理 / 生成树计数

论文《生成树的计数及其应用》学习博客
 推荐阅读博客

Kirchhoff 矩阵树定理 / Matrix-Tree 定理，用来解决一张图的生成树计数问题

首先我们要知道生成树计数问题是什么：就是给你一个n个点,m条边的图，问你这个图的生成树个数。而矩阵树定理就是高效解决这一问题的算法。

定义：

图的度数矩阵 D[][]是n*n的矩阵，i = j 时 D[i][j]=Vi的度数，否则D[i][j] = 0。
图的邻接矩阵 A[][]是n*n的矩阵，vi, vj 间有边时 A[i][j] = 1, 否则 A[i][j] = 0。
定义图的Kirchhoff矩阵为 (K[i][j] = D[i][j] - A[i][j])

举例：[图源学习博客]

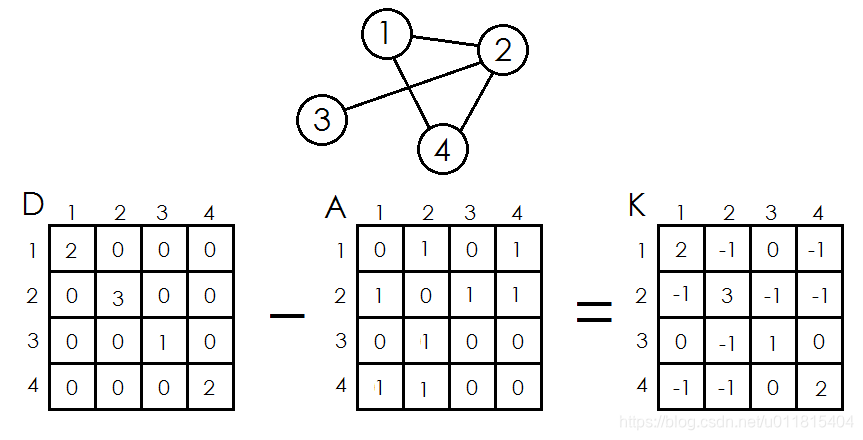
矩阵树定理：

对一个图G求出其Kirchhoff矩阵，该矩阵的n-1阶主子式的行列式绝对值为生成树的个数。也就是把该矩阵任意一行一列去掉后得到的矩阵的行列式的绝对值就是该图生成树的个数。

证明见上面论文链接。

代码模板：

ll k[N][N];
ll gauss(int n){   //其实就是在模拟求n-1阶行列式值的过程
    ll res = 1;
    for(int i = 1; i <= n - 1; ++ i){
        for(int j = i + 1; j <= n - 1; ++ j){
            while(k[i][j]){
                int t = k[i][i] / k[j][i];
                for(int z = i; z <= n - 1; ++ z){
                    k[i][z] = (k[i][z] - t * k[j][z] + mod) % mod;
                	swap(k[i][z], k[j][z]);
                }
                res = -res;
            }
        }
        res = (res * k[i][i]) % mod;
    }
    return (res + mod) % mod;
}

给定m条边求图的Kirchhoff矩阵

for(int i = 1; i <= m; ++ i){
    int x, y; scanf("%d%d", &x, &y);
    k[x][x] ++; k[y][y] ++;         //得到Kirchhoff矩阵
    k[x][y] --; k[y][x] --;
}

例题 uva10766

luogu题目链接

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<queue>
#include<vector>
#include<string>
#include<fstream>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i)
#define per(i, a, n) for(int i = n; i >= a; -- i)
typedef long long ll;
typedef pair<ll, int>PII;
const int N = 60;
const ll mod = 1e9 + 7;
const double Pi = acos(- 1.0);
const int INF = 0x3f3f3f3f;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
//

int n, m;
ll k[N][N];
bool vis[N][N];

ll gaus(int n){
    ll res = 1;
    for(int i = 1; i <= n - 1; ++ i){
        for(int j = i + 1; j <= n - 1; ++ j){
            while(k[j][i]){
                ll t = k[i][i] / k[j][i];
                for(int z = i; z <= n - 1; ++ z){
                    k[i][z] = (k[i][z] - t * k[j][z]);
                    swap(k[i][z], k[j][z]);
                }
                res = -res;
            }
        }
        res = (res * k[i][i]);
    }
    return res;
}

int main()
{
    int T;
    while(~scanf("%d%d%d",&n,&m,&T)){
        memset(vis, false, sizeof(vis));
        for(int i = 1; i <= m; ++ i){
            int x, y; scanf("%d%d",&x,&y);
            vis[x][y] = true;
            vis[y][x] = true;
        }
        memset(k, 0, sizeof(k));
        for(int i = 1; i <= n; ++ i){
            for(int j = 1; j <= n; ++ j){
                if(j == i || vis[i][j]) continue;
                k[i][i] ++;
                k[i][j] --;
            }
        }
        ll res = gauss(n);
        printf("%lld
",res);
    }
    return 0;
}