【题解】[SDOI2008] 烧水问题 By 5ab as a juruo.

题目
分析
- 证明
  - 第一部分
  - 第二部分
Code

题目

题目来源：CCF 山东省选 2008；

在线评测：Luogu#1984。

题目描述

把总质量为 (1 extrm{kg}) 的水分装在 (n) 个杯子里，每杯水的质量均为 (left(dfrac{1}{n} ight) extrm{kg})，初始温度均为 (0; {}^circ! extrm{C})。现需要把每一杯水都烧开。

我们可以对任意一杯水进行加热。把一杯水的温度升高 (t; {}^circ! extrm{C}) 所需的能量为 (dfrac{4200 t}{n}\, extrm{J})，其中，J 是能量单位“焦耳”。如果一旦某杯水的温度达到 (100; {}^circ! extrm{C})，那么这杯水的温度就不能再继续升高，此时我们认为这杯水已经被烧开。显然地，如果直接把水一杯一杯地烧开，所需的总能量为 (4200 imes 100=4.2 imes 10^5)。

在烧水的过程中，我们随时可以在两杯温度不同的水之间进行热传递操作。热量只能从温度较高的那杯水传递到温度较低的那杯水。由于两杯水的质量相同，所以进行热传递操作之后，原来温度较高的那杯水所降低的温度总是等于原来温度较低的那杯水所升高的温度。

一旦两杯水的温度相同，热传递立刻停止。

为了把问题简化，我们假设：

1、没有进行加热或热传递操作时，水的温度 不会变化。
2、加热时所花费的能量全部被水吸收，杯子 不吸收能量。
3、热传递总是隔着杯子进行，(n) 杯水永远不会互相混合。
4、热传递符合能量守恒，而且没有任何的热量损耗。

在这个问题里，只要求把 每杯水都至少烧开一遍 就可以了，而不要求最终每杯水的温度都是 (100; {}^circ! extrm{C})。我们可以用如下操作把两杯水烧开：先把一杯水加热到 (100; {}^circ! extrm{C})，花费能量 (dfrac{4200 imes 100}{2}\, extrm{J})，然后两杯水进行热传递，直到它们的温度都变成 (50; {}^circ! extrm{C}) 为止，最后把原来没有加热到 (100; {}^circ! extrm{C}) 的那杯水加热到 (100; {}^circ! extrm{C})，花费能量 (dfrac{4200 imes 100}{2 imes 2}\, extrm{J})，此时两杯水都被烧开过了，当前温度一杯 (100; {}^circ! extrm{C})，一杯 (50; {}^circ! extrm{C})，花费的总能量为 (4200 imes 75\, extrm{J})，比直接烧开所需的 (4200dfrac 100\, extrm{J}) 少花费了 (25\%) 的能量。

你的任务是设计一个最佳的操作方案使得 (n) 杯水都至少被烧开一遍所需的总能量最少。

输入格式

输入文件只有一个数 (n)。

输出格式

输出 (n) 杯水都至少被烧开一遍所需的最少的总能量，单位为 ( extrm{J})，四舍五入到小数点后两位。

数据规模及约定

(1le nle 3 imes 10^6)

分析

题意是将 (n) 杯水加热 (100; {}^circ! extrm{C})，每杯水只需加热到一次即可。中途可以让任意两杯水进行热量交换，使其在和不变的前提下温度相等。求最少消耗的能量。

这是一道结论题。我们不妨模拟一下找找规律：

首先，只有一杯水，那就直接加热：

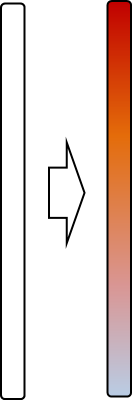
有两杯水，那么就先加热一杯，然后再给另一边传热即可：

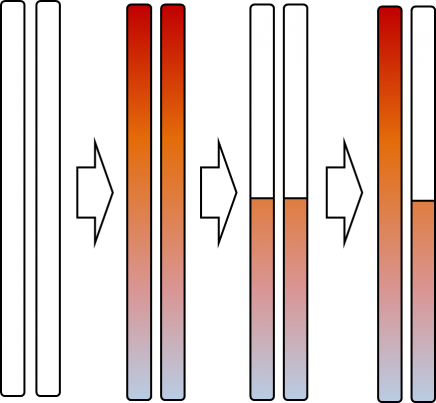
那么，如果有三杯水呢？

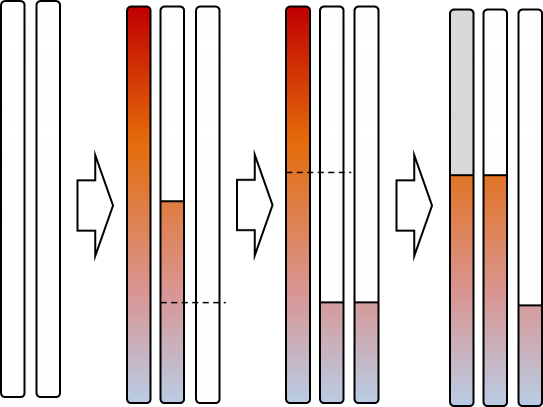
首先，肯定要先加热一杯水，然后再用这一杯水的热量来辅助加热第二杯水。这些过程是一定的。我们的目标是尽量让第三杯水加热所需的热量尽量少。

所以，我们优先用传热的方式对第三杯水进行加热。在这过程中，我们发现：先用温度低的水进行传热，然后用较热的水传热，可以使最终的温度尽量高。

~~（稍微感性地理解一下吧）~~

证明

那么，为什么这样做是对的呢？

我们要证明两部分：

对于 (n) 杯的情况，要从前面的情况转移；
对于一个固定的杯数，传递温度都要从小开始。

第一部分

对于 (n) 杯的情况，一定可以通过以下几个步骤：

完成 (n-1) 杯的情况；
用前 (n-1) 杯的余热给这一杯传递；
加热剩下这一杯。

如果 (a_n) 不从 (a_{n-1}) 进行转移而更优，必然导致加热最后一杯所需要的能量少得多。

但是注意，加热最后一杯需要的能量少，说明前面加热需要更多的能量。而根据热量的转移效果折半，导致这样做并没有直接给最后一杯加热更优，矛盾。

所以，(a_n) 就一定是从 (a_{n-1}) 转移的。

第二部分

接下来我们要证明：转移时按照从小到大的顺序，可以传递最多的热量。

对于剩余温度最高的那杯水，显然要让尽可能高温度的水和它合并，才能使最终的答案温度最高。

接下来，对于温度次高的水，一样地可以得出类似的结论。递归即证。

对于这种情况，我们考虑如何计算。定义 (a_n) 为 (n) 杯水的答案。

为了方便求解，我们定义 (b_n) 为当 (n) 杯水时，加热最后一杯水所需要的热量。易得 (large{a_n=sum b_n})。

那么 (b_n) 怎么计算呢？考虑热量转移时的情况：

对于 (a_1)，(left<c_1 ight>=left<c ight>)，(b_1=c)；
对于 (a_2)，(left<c_2 ight>=left<dfrac{c}{2},c ight>)，(b_2=dfrac{c}{2})；
对于 (a_3)，(left<c_3 ight>=left<dfrac{c}{4},dfrac{5c}{8},c ight>)，(b_3=dfrac{3c}{8})；
对于 (a_4)，(left<c_4 ight>=left<dfrac{c}{8},dfrac{3c}{8},dfrac{11c}{16},c ight>)，(b_4=dfrac{5c}{16})

我们容易发现，(c_{i,j}=dfrac{c_{i-1,j}+c_{i,j-1}}{2})，(b_n=c-c_{n,n-1})，将其展开得：

[egin{aligned} b_n=c-c_{n,n-1} & =c-left( dfrac{1}{2} c_{n,n-2} + dfrac{1}{2} c_{n-1,n-1} ight) \ & =c-left( dfrac{1}{4} c_{n,n-3} +dfrac{1}{4} c_{n-1,n-2} + dfrac{1}{2} c_{n-1,n-1} ight) \ & =dots \ & =c-left(dfrac{1}{2^{n-2}} c_{n,1}+sumlimits_{i=2}^{n-1}dfrac{1}{2^{n-i}} c_{n-1,i} ight) \ & =c-left(sumlimits_{i=1}^{n-1}dfrac{1}{2^{n-i}} c_{n-1,i} ight) end{aligned} ]

再从能量守恒的角度，可以得到 (large{sum c_i-sum c_{i-1}=b_i})

最后我们可以得到：~~（我可以很不要脸地说这个公式是我用 OEIS 查出来的吗）~~

[b_n=dfrac{dbinom{2n-1}{n}}{2^{2n-1}} ]

我们可以直接求这个公式，或者我们可以递推：

[egin{aligned} dfrac{b_n}{b_{n-1}}= & dfrac{frac{inom{2n-1}{n}}{2^{2n-1}}}{frac{inom{2(n-1)-1}{n-1}}{2^{2(n-1)-1}}}\ =&dfrac{inom{2n-1}{n}2^{2n-3}}{inom{2n-3}{n-1}2^{2n-1}}\ =&dfrac{(2n-1)!(n-1)!(n-2)!2^{2n-3}}{(2n-3)!n!(n-1)!2^{2n-1}}\ =&dfrac{(2n-2)(2n-1)}{4n(n-1)}\ =&dfrac{2n-1}{2n} end{aligned} ]

这样我们就可以很快地求出答案。

Code

#include <cstdio>
using namespace std;

const double tot = 420000;

int main()
{
	int n;
	double sing = 0, cut;

	scanf("%d", &n);

	cut = tot / n;
	for (int i = 1; i <= n; i++)
	{
		sing += cut;
		cut *= double(i * 2 - 1) / double(i * 2);
	}
	printf("%.2lf
", sing);
	
	return 0;
}
```b