一、范数
L1、L2这种在机器学习方面叫做正则化,统计学领域的人喊她惩罚项,数学界会喊她范数。
L0范数 表示向量xx中非零元素的个数。
L1范数 表示向量中非零元素的绝对值之和。
L2范数 表示向量元素的平方和再开平方
在p范数下定义的单位球(unit ball)都是凸集(convex set,简单地说,若集合A中任意两点的连线段上的点也在集合A中,则A是凸集),但是当0<p<1时,在该定义下的unit ball并不是凸集(注意:我们没说在该范数定义下,因为如前所述,0<p<1时,并不是范数).下图展示了p取不同值时unit ball的形状

二、正则化
L1正则化,又叫Lasso Regression
如下图所示,L1是向量各元素的绝对值之和
L2正则化,又叫Ridge Regression
如下图所示,L2是向量各元素的平方和
对于上面的两种情况做一下简单推广,可以得到更为一般的形式:
上式前半部分为原有的损失函数,后半部分为正则项。其中,q=1时即为L1正则化,q=2为L2正则化。
三、lasso和ridge回归
Lasso Regresssion
Lasso Regresssion使用的就是L1正则化, 下面就是Lasso Regression 的Loss Function的样子,是不是很美丽:
公式(1)
注:β0是常数项
简单说一下,第一个SUM(∑)里面可以看出来是一个线性回归求损失平方,第二个SUM(∑)是线性回归中系数的服从条件,用来约束解的区域,凸优化中的约束求解一般都长这个样子。
此外,Lasso Regression的整体损失求极小的样子改成拉格朗日形式就是下面这个式子的模样:
公式(2)
从式子里可以看到回归系数使用的是L1正则化,λ是惩罚参数或者叫做调节参数。L1范数的好处是当惩罚参数充分大时可以把某些待估的回归系数精确地收缩到0。
Lasso以缩小变量集(降阶)为思想,是一种收缩估计方法。Lasso方法可以将变量的系数进行压缩并使某些回归系数变为0,进而达到变量选择的目的,可以广泛的应用于模型改进与选择。我们通过选择惩罚函数,借用Lasso思想和方法实现变量选择的目的。
在建立模型之初,为了尽量减小因缺少重要自变量而出现的模型偏差,通常会选择尽可能多的自变量。然而,建模过程需要寻找对因变量最具有强解释力的自变量集合,也就是通过自变量选择(指标选择、字段选择)来提高模型的解释性和预测精度。指标选择在统计建模过程中是极其重要的问题。Lasso算法则是一种能够实现指标集合精简的估计方法。
公式(1)理解:
lasso estimate具有shrinkage和selection两种功能,shrinkage这个不用多讲,本科期间学过回归分析的同学应该都知道岭估计会有shrinkage的功效,lasso也同样。关于selection功能,Tibshirani提出,当t值小到一定程度的时候,lasso estimate会使得某些回归系数的估值是0,这确实是起到了变量选择的作用。当t不断增大时,选入回归模型的变量会逐渐增多,当t增大到某个值时,所有变量都入选了回归模型,这个时候得到的回归模型的系数是通常意义下的最小二乘估计。从这个角度上来看,lasso也可以看做是一种逐步回归的过程。
模型选择本质上是寻求模型稀疏表达的过程,而这种过程可以通过优化一个“损失”+“惩罚”的函数问题来完成。
这里公式(1)和公式(2)的λ和t是一一对应关系。
公式(2)中的λ是重要的设置参数,它控制了惩罚的严厉程度,如果设置得过大,那么最后的模型参数均将趋于0,形成拟合不足。如果设置得过小,又会形成拟合过度。
λ求法
通常使用交叉验证法(CV)或者广义交叉验证(GCV),当然也可以使用AIC、BIC等指标。
交叉验证法:对λ的格点值,进行交叉验证,选取交叉验证误差最小的λ值。最后,按照得到的λ值,用全部数据重新拟合模型即可。
对参数引入 拉普拉斯先验 等价于 L1正则化。
(根据斜率可以发现l1在小的时候惩罚力度还很大)

RidgeRegression 岭回归
岭回归使用的是L2正则化,下面的式子就是Ridge Regression的Loss Function 的美丽容颜:
式子的最后面是L2正则项,系数的平方和。上式的等价问题如下:
最小二乘估计是最小化残差平方和(RSS):
岭回归在最小化RSS的计算里加入了一个收缩惩罚项(正则化的l2范数)
这个惩罚项中lambda大于等于0,是个调整参数。各个待估系数越小则惩罚项越小,因此惩罚项的加入有利于缩减待估参数接近于0。
重点在于lambda的确定,可以使用交叉验证或者Cp准则。
对参数引入 高斯先验 等价于L2正则化
链接·:http://blog.csdn.net/SzM21C11U68n04vdcLmJ/article/details/78138887
四、 L1和L2正则化的异同
1. L2 regularizer :使得模型的解偏向于 norm 较小的 W,通过限制 W 的 norm 的大小实现了对模型空间的限制,从而在一定程度上避免了 overfitting 。不过 ridge regression 并不具有产生稀疏解的能力,得到的系数仍然需要数据中的所有特征才能计算预测结果,从计算量上来说并没有得到改观。
2. L1 regularizer : 它的优良性质是能产生稀疏性,导致 W 中许多项变成零。 稀疏的解除了计算量上的好处之外,更重要的是更具有“可解释性”。
lasso regression和ridge regression比较:
这两种方法的共同点在于,将解释变量的系数加入到Cost Function中,并对其进行最小化,本质上是对过多的参数实施了惩罚。
而两种方法的区别在于惩罚函数不同。但这种微小的区别却使LASSO有很多优良的特质(可以同时选择和缩减参数)。
岭回归的一个缺点:在建模时,同时引入p个预测变量,罚约束项可以收缩这些预测变量的待估系数接近0,但并非恰好是0(除非lambda为无穷大)。这个缺点对于模型精度影响不大,但给模型的解释造成了困难。这个缺点可以由lasso来克服。(所以岭回归虽然减少了模型的复杂度,并没有真正解决变量选择的问题) 。具体可以看上面ridge参数选取图
可以看到,L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现,而目标函数的测地线除非位置摆得非常好,大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性,例如图中的相交点就有w1=0,而更高维的时候(想象一下三维的L1-ball 是什么样的?)除了角点以外,还有很多边的轮廓也是既有很大的概率成为第一次相交的地方,又会产生稀疏性。
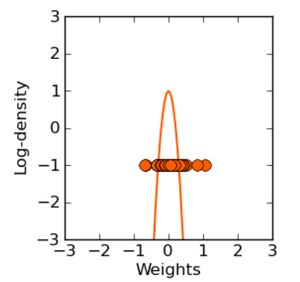
L2正则项作用是限制权重W过大,且使得权重W分布均匀。而L1正则项倾向于得到离散的W,各W之间差距较大。
五、特征选择
当我们使用数据训练分类器的时候,很重要的一点就是要在过度拟合与拟合不足之间达成一个平衡。
防止过度拟合的一种方法就是对模型的复杂度进行约束。模型中用到解释变量的个数是模型复杂度的一种体现。
控制解释变量个数有很多方法,例如特征选择(feature selection),即用filter或wrapper方法提取解释变量的最佳子集。
或是进行特征构造(feature construction),即将原始变量进行某种映射或转换,如主成分方法和因子分析。
特征选择的方法是比较“硬”的方法,变量要么进入模型,要么不进入模型,只有0-1两种选择。
但也有“软”的方法,也就是Regularization类方法,例如岭回归(Ridge Regression)和套索方法(LASSO:least absolute shrinkage and selection operator)
链接:回归系列之L1和L2正则化



