NOIP前恶补数论的感觉真是神清气爽啊!
教练问我们有什么知识点不会,一问到数论马上就GG了。
花了2个小时学习中国剩余定理。
好了废话少说,我们进入正题。
首先膜拜一下中国南北朝时期的数学家孙子(不是孙武)。
用现代数学的语言来说明的话,中国剩余定理给出了以下的一元线性同余方程组:
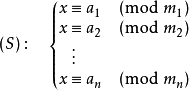
求最小的正整数解x。
当m1--mn相互互质时可以求解(若不互质可以通过扩展中国剩余定理求解)。
分几步求解:
1.求一下∏ni=1mi记为m
2.设Mi=m/mi
3.设ti满足Mi$ imes$ti≡1(mod mi)
4.x=∑ni=1Mi$ imes$ai$ imes$ti
至于第四步的原因
因为我们保证Mi是除了当前mi之外所有模数的倍数,所以我们的第4步的理论依据是对于任意K(K≠i),Mi$ imes$ai$ imes$ti ≡ 0(mod mk),所以Mi$ imes$ai$ imes$ti≡ai(mod mi).所以第4步成立。
问题来了,Mi和ai好办,如何求ti?
我们注意到Mi$ imes$ti≡1(mod mi)。考虑扩展GCD,把它转换成ax+by=1解同余方程。
void exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b)
{
x=1;
y=0;
return;
}
exgcd(b,a%b,x,y);
ll tmp=x;
x=y,y=tmp-a/b*y;
return ;
}
解完之后,就可以求辣!
ll China()
{
ll x,ans=0,y;
for(int i=1;i<=n;i++)
m*=in[i];
for(int i=1;i<=n;i++)
{
M[i]=m/in[i];
exgcd(M[i],in[i],x,y);
ans=(ans+a[i]*x*M[i])%m;
}
return (ans+m)%m;
}
中国剩余定理最基础题目的网站https://neooj.com:8082/oldoj/problem.php?id=1322
上代码
#include<cstdio>
typedef long long ll;
ll M[11];
ll t[11];
ll a[11];
ll in[11];
ll m=1;
ll n;
void exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b)
{
x=1;
y=0;
return;
}
exgcd(b,a%b,x,y);
ll tmp=x;
x=y,y=tmp-a/b*y;
return ;
}
ll China()
{
ll x,ans=0,y;
for(int i=1;i<=n;i++)
m*=in[i];
for(int i=1;i<=n;i++)
{
M[i]=m/in[i];
exgcd(M[i],in[i],x,y);
ans=(ans+a[i]*x*M[i])%m;
}
return (ans+m)%m;
}
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
scanf("%lld%lld",&in[i],&a[i]);
ll ans=China();
printf("%lld",ans);
}
下面讲解扩展Lucas定理。
普通的Lucas定理长这样:
C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p(p为质数)
上个代码
#include<cstdio>
#define mod 10007
int fac[mod+2];
int inv[mod+2];
int lucas(long long n,long long m)
{
if(n<m)
return 0;
if(n<mod&&m<mod)
return fac[n]*inv[m]%mod*inv[n-m]%mod;
return lucas(n%mod,m%mod)*lucas(n/mod,m/mod)%mod;
}
int main()
{
fac[0]=1,inv[mod-1]=mod-1;
for(int i=1;i<=mod;i++) fac[i]=fac[i-1]*i%mod;
for(int i=mod-2;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
long long n,m;
scanf("%I64d%I64d",&n,&m);
printf("%d
",lucas(n,m));
}
对于p不是质数的情况我们可以向中国剩余定理的方向讨论。
若不是素数,将p分解质因数,将C(n,m)分别按照Lucas的方法求对p的质因数的模,然后用中国剩余定理合并。比如计算C(10,3)%14。C(10,3)=120,14有两个质因数2和7,120%2=0,120%7=1,这样用(2,0)(7,1)找到最小的正整数8即是答案,即C(10,3)%14=8非常简单。注意,这里只适用于p分解完质因数后每个质因数只出现一次.至于多次的,我不会(大写GG,有兴趣的可以学习一下.)
EX中国剩余定理
因为模数不是质数,所以我们采用两两合并的思想。
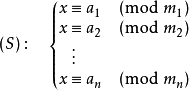
x=a1+m1$ imes$y1
x=a2+m2$ imes$y2
两方程联立,x≡a1+m1$ imes$y1(mod lcm(m1,m2))
蒋神blog中有证明
https://www.cnblogs.com/ShuraK/p/7905790.html##11
上code:P4777 【模板】扩展中国剩余定理(EXCRT)
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b)
{
x=1;
y=0;
return a;
}
ll gcd=exgcd(b,a%b,x,y);
ll tmp=x;
x=y;
y=tmp-a/b*y;
return gcd;
}
ll pow(ll x,ll y,ll mod)
{
ll ans=0;
while(y)
{
if(y&1)
ans=(ans+x)%mod;
x=(x+x)%mod;
y/=2;
}
return ans;
}
ll China()
{
ll M=m[1];
ll ans=a[1];
for(int i=2;i<=n;i++)
{
ll A=M,B=m[i],d=((a[i]-ans)%B+B)%B,x,y;
ll gcd=exgcd(A,B,x,y);
x=pow(x,d/gcd,B/gcd);
M*=B/gcd;
ans=(ans+x*A)%M;
}
return (ans%M+M)%M;
}