素数筛法
如果我们想要知道小于等于 n有多少个素数呢?
一个自然的想法是我们对于小于等于n的每个数进行一次判定。这种暴力的做法显然不能达到最优复杂度,考虑如何优化。
考虑这样一件事情:如果x是合数,那么x的倍数也一定是合数。利用这个结论,我们可以避免很多次不必要的检测。
如果我们从小到大考虑每个数,然后同时把当前这个数的所有(比自己大的)倍数记为合数,那么运行结束的时候没有被标记的数就是素数了。
int Eratosthenes(int n) { int p = 0; for (int i = 0; i <= n; ++i) is_prime[i] = 1; is_prime[0] = is_prime[1] = 0; for (int i = 2; i <= n; ++i) { if (is_prime[i]) { prime[p++] = i; // prime[p]是i,后置自增运算代表当前素数数量 for (int j = i * i; j <= n; j += i) // 因为从 2 到 i - 1 的倍数我们之前筛过了,这里直接从 i // 的倍数开始,提高了运行速度 is_prime[j] = 0; //是i的倍数的均不是素数 } } return p; }
以上为 Eratosthenes 筛法 (埃拉托斯特尼筛法),时间复杂度是 O(nlognlogn)。
但显然有重复被标记的,所以无法达到线性。
线性筛法代码:
void init() { phi[1] = 1; for (int i = 2; i < MAXN; ++i) { if (!vis[i]) { phi[i] = i - 1; pri[cnt++] = i; } for (int j = 0; j < cnt; ++j) { if (1ll * i * pri[j] >= MAXN) break; vis[i * pri[j]] = 1; if (i % pri[j]) { phi[i * pri[j]] = phi[i] * (pri[j] - 1); } else { // i % pri[j] == 0 // 换言之,i 之前被 pri[j] 筛过了 // 由于 pri 里面质数是从小到大的,所以 i 乘上其他的质数的结果一定也是 // pri[j] 的倍数 它们都被筛过了,就不需要再筛了,所以这里直接 break // 掉就好了 phi[i * pri[j]] = phi[i] * pri[j]; break; } } } }
上面的这种 线性筛法 也称为 Euler 筛法 (欧拉筛法)。
注意到筛法求素数的同时也得到了每个数的最小质因子。
筛法求欧拉函数
注意到在线性筛中,每一个合数都是被最小的质因子筛掉。比如设p1是n的最小质因子,n'=n/p1 ,那么线性筛的过程中n通过n'*p筛掉。
观察线性筛的过程,我们还需要处理两个部分,下面对 n'modp1分情况讨论。
如果n'modp1=0,那么 n'包含了n的所有质因子。
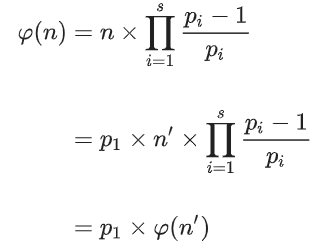
那如果n'modp1!=0 呢,这时n'和 n是互质的,根据欧拉函数性质,我们有:
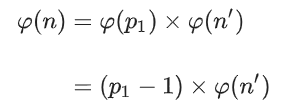
void phi_table(int n, int* phi) { for (int i = 2; i <= n; i++) phi[i] = 0; phi[1] = 1; for (int i = 2; i <= n; i++) if (!phi[i]) for (int j = i; j <= n; j += i) { if (!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i - 1); } }
筛法求莫比乌斯函数
线性筛
void pre() { mu[1] = 1; for (int i = 2; i <= 1e7; ++i) { if (!v[i]) mu[i] = -1, p[++tot] = i; for (int j = 1; j <= tot && i <= 1e7 / p[j]; ++j) { v[i * p[j]] = 1; if (i % p[j] == 0) { mu[i * p[j]] = 0; break; } mu[i * p[j]] = -mu[i]; } }
筛法求约数个数
void pre() { d[1] = 1; for (int i = 2; i <= n; ++i) { if (!v[i]) v[i] = 1, p[++tot] = i, d[i] = 2, num[i] = 1; for (int j = 1; j <= tot && i <= n / p[j]; ++j) { v[p[j] * i] = 1; if (i % p[j] == 0) { num[i * p[j]] = num[i] + 1; d[i * p[j]] = d[i] / num[i * p[j]] * (num[i * p[j]] + 1); break; } else { num[i * p[j]] = 1; d[i * p[j]] = d[i] * 2; } } } }
筛法求约数和
fi表示i的约数和,gi表示i的最小质因子的和


void pre() { g[1] = f[1] = 1; for (int i = 2; i <= n; ++i) { if (!v[i]) v[i] = 1, p[++tot] = i, g[i] = i + 1, f[i] = i + 1; for (int j = 1; j <= tot && i <= n / p[j]; ++j) { v[p[j] * i] = 1; if (i % p[j] == 0) { g[i * p[j]] = g[i] * p[j] + 1; f[i * p[j]] = f[i] / g[i] * g[i * p[j]]; break; } else { f[i * p[j]] = f[i] * f[p[j]]; g[i * p[j]] = 1 + p[j]; } } } for (int i = 1; i <= n; ++i) f[i] = (f[i - 1] + f[i]) % Mod; }
总结:这些筛法都是基于素数的线性筛,因为这些函数对于素数来说都是是积性函数。