

雅克比矩阵将机器人关节空间的速度映射到笛卡尔空间的末端速度。
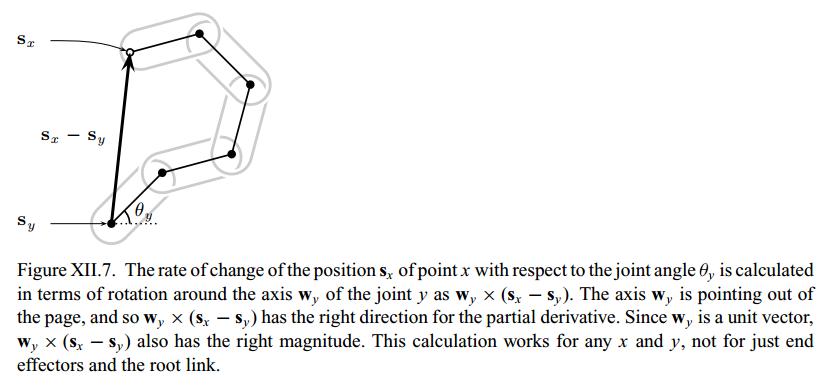
从上图可以看出,只考虑关节y的旋转(假定其它关节固定不动,在某一时刻关节y变化一个微小的角度ϕ--注意联系偏微分的定义),则末端将绕着y以||sx− sy||为半径旋转,末端速度为:ϕwy × (sx− sy),则可以推出雅克比矩阵J中关于关节y的那一列为:∂sx /∂θy=wy × (sx− sy)
We want to find a way to change the joint angles so as to move the links’ positions closer to the desired positions. This process can be iterated in such a way that each iteration moves the links’ positions closer to their target positions until eventually new joint positions are reached that place the links close enough to their desired positions. The reason for using an iterative procedure is that it is usually too complicated to actually solve for joint angles,θ , in terms of the desired link positions. The iterative procedure will be easier to implement and, if it converges sufficiently well, can provide values for the joint angles that put the links arbitrarily close to their desired positions. For a single step of the iterative procedure, we consider the function telling us how links’ positions depend on joint angles. We then evaluate the partial derivatives of this function to find a linear approximation to the function. That is, we compute the rates of changes in links’ positions with respect to the rates of changes in joint angles. These give a Jacobian matrix of partial derivatives. With some assumptions about the nonsingularity of the Jacobian matrix, we can then find a way to change the joints’ angles so as to move the links’ positions closer to the desired positions. Since the Jacobian gives only a linear approximation to the function, we have to iterate the process until it converges to a good solution.
The first step in setting up the inverse kinematics problem is to define the Jacobian matrix, which will tell us how the position of x changes with respect to small changes in the angles θ; in other words, the matrix will contain the partial derivatives of sx withrespect to the variables θ .

If the joint y is translational, the entry in the Jacobian matrix is even easier to compute. Suppose the joint performs translation the direction of the unit vector wy , so that the the joint “angle” measures distance moved in the direction wy. Then if the end effector is affected by the joint, we have ∂sx /∂θy=wy 。即如果该关节为移动关节,则雅克比矩阵中这一列为移动副的方向向量wy。
To see that this correctly defines the partial derivative, note the following: (a) If x is not a proper descendant of y, then the rotation of y’s joint does not affect the position of x,and so ∂sx /∂θy = 0. (b) Otherwise, the vector from point y to point x is equal to sx− sy,and the rotation axis for angle θy is the axis wy. An infinitesimal rotation ϕ radians around the axis wy centered at sy will move the point x an infinitesimal distance given by the vector ϕwy × (sx− sy). From this observation, the second part of the definition of ∂sx /∂θy is obtained immediately. Figure XII.7 shows how to visualize the derivation of the formula for the partial derivative.
即如果末端x不受关节y的影响,如情形(a) ;或者关节y正位于机器人末端,则∂sx /∂θy = 0。 sy为关节y的位置向量,wy为单位向量,其指向沿着关节的轴线方向,in this case, if angles are measured in radians with the direction of rotation given by the right rule and if the end effector is affected by the joint, then the corresponding entry in the Jacobian is wy × (sx− sy)


参考:
1. 3-D Computer Graphics: A Mathematical Introduction with OpenGL, Cambridge University Press, 2003 Ch. 12
2. John J.Craig. Introduction to Robotics Mechanics and Control