Re.常系数齐次递推

前言

嗯我之前的不知道多少天看这个的时候到底在干什么呢

为什么那么。。可能大佬们太强的缘故

最后仔细想想思路那么的emmm

不说了要落泪了

唔唔唔

前置

多项式求逆

多项式除法/取模

常系数齐次递推目的

求一个满足

$即:$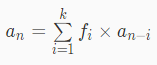

给出f1--fk,a₀--a_k-1求a_n

N=1e9,K=32000

常系数齐次递推主要思路

emmm矩阵快速幂怎么样都应该会的

设转移矩阵为A,st=[a₀,a₁...a_k-2,a_k-1]为初始矩阵

显然a_n=(st*Aⁿ)₀

O(k³logn)和O(k²logklogn)的矩阵快速幂在此范围下显然太暴力了

发现k过大时时间复杂度主要花在矩阵乘法上

考虑如何不用矩阵通过多项式来计算答案

先考虑把Aⁿ转化为A⁰--A^k-1组合出来的和

设Aⁿ=Q(A)*G(A)+R(A)

Q,G,R是以矩阵为x(参数)的多项式

当强制G的多项式的最高次数为k次方

那么可写成Aⁿ=Q(A)*G(A)+c_iA^_i

此时如果再强制试使得G(A)为0时

那么Q(A)*G(A)=0

Aⁿ=c_iA^_i=R(A)

所以c_iA^_i=Aⁿ%G(A)

通过多项式取模就可将Aⁿ转化为c_iA^_i

通过上面的推导发现a_n=(st*A_n)₀=(st*c_iA^_i)₀=(c_iA^_ist)₀

因为我们每次只取矩阵的第0项每转移一次下一项就往上移一个位置原来的第0项就去掉

所以A^_ist就等于st_i

最后的a_n=c_ist_i

这样只要找出之前要求的那个G(A)就可以O(k)得出答案了

那么如何求出G(A)

设G(A)=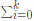g_iAⁱ=0

这里有个我暂时不会的结论

如果递推系数为f₁--f_n

那么g_k-i=f_i,g_k=1

所以最后流程就是

1.求出G(A)

2.用快速幂和多项式取模求出Aⁿ在模G(A)时的余数R(A) 也就是把Aⁿ转化为A¹--A^k的组合

3.计算答案aⁿ=c_ist_i

代码

这时隔多年我中于调出来了一份常数巨大的代码

 #include<bits/stdc++.h> 
using namespace std;
#define ll long long
#define C getchar()-48
inline ll read()
{
    ll s=0,r=1;
    char c=C;
    for(;c<0||c>9;c=C) if(c==-3) r=-1;
    for(;c>=0&&c<=9;c=C) s=(s<<3)+(s<<1)+c;
    return s*r;
} 
const int p=998244353,G=3,N=140010;
int n,k,mx,cs,qvq,tz;
ll rev[N];
ll f[N],st[N],g[N],invg[N];
ll tmp[N],tmp1[N],tmp2[N],tmpa[N],tmpb[N];
ll a[N],ans[N];
inline ll ksm(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%p;
        a=(a*a)%p;
        b>>=1;
    }
    return ans;
} 
inline void ntt(ll *a,ll n,ll kd)
{
    for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
    for(int i=1;i<n;i<<=1)
    {
        ll gn=ksm(G,(p-1)/(i<<1));
        for(int j=0;j<n;j+=(i<<1))
        {
            ll t1,t2,g=1;
            for(int k=0;k<i;k++,g=g*gn%p)
            {
                t1=a[j+k],t2=g*a[j+k+i]%p;
                a[j+k]=(t1+t2)%p,a[j+k+i]=(t1-t2+p)%p;
            } 
        }
    }
    if(kd==1) return;
    ll ny=ksm(n,p-2);
    reverse(a+1,a+n);
    for(int i=0;i<n;i++) a[i]=a[i]*ny%p;
} 
inline void cl(ll *a,ll *b,ll n,ll m,ll len,ll w)
{
    for(int i=0;i<len;i++) tmp1[i]=i<n?a[i]:0;
    for(int i=0;i<len;i++) tmp2[i]=i<m?b[i]:0;
    for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(w-1));
}
inline void polyinv(ll *a,ll *b,ll ed)
{
    b[0]=ksm(a[0],p-2);
    for(int k=1,j=0;k<=(ed<<1);k<<=1,j++)
    {
        ll len=k<<1;
        cl(a,b,k,k,len,j+1);
        ntt(tmp1,len,1);ntt(tmp2,len,1);
        for(int i=0;i<len;i++) b[i]=tmp2[i]*(2ll-tmp1[i]*tmp2[i]%p+p)%p;
        ntt(b,len,-1);
        for(int i=k;i<len;i++) b[i]=0;
    }
}
inline void polymul(ll *a,ll *b,ll *c,ll n,ll m)
{
    ll len=1,w=0;
    while(len<=(n+m)) len<<=1,w++;
    cl(a,b,n,m,len,w);
    ntt(tmp1,len,1);ntt(tmp2,len,1);
    for(int i=0;i<len;i++) c[i]=tmp1[i]*tmp2[i]%p;
    ntt(c,len,-1);
}
inline void polymod(ll *a,ll n=mx<<1,ll m=k)
{                   
    int ed=(mx<<1);while(a[--ed]==0);if(ed<k) return; 
    
    n=ed;
    reverse(a,a+1+n);
    polymul(a,invg,tmpa,n+1,n-m+1);    
    reverse(tmpa,tmpa+n-m+1);
    reverse(a,a+1+n);
    
    polymul(g,tmpa,tmpb,m+1,n-m+1);
    for(int i=0;i<k;i++) a[i]=(a[i]-tmpb[i]+p)%p;
    for(int i=k;i<=ed;i++)a[i]=0;
    for(int i=0;i<(mx<<1);i++) tmpa[i]=tmpb[i]=0;
}
int main()
{
    n=read(),k=read();mx=1,cs=0;
    while(mx<=k) mx<<=1,cs++;
    for(int i=1;i<=k;i++) f[i]=read(),f[i]=f[i]<0?f[i]+p:f[i];
    for(int i=0;i<k;i++) st[i]=read(),st[i]=st[i]<0?st[i]+p:st[i];
    for(int i=1;i<=k;i++) g[k-i]=p-f[i];g[k]=1;
    for(int i=0;i<=k;i++) tmp[i]=g[i];
    
    reverse(tmp,tmp+1+k);
    polyinv(tmp,invg,mx);
    for(int i=mx;i<=(mx<<1);i++) invg[i]=0;
    for(int i=0;i<=k;i++) tmp[i]=0;
    for(int i=0;i<(mx<<1);i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(cs+1-1));
    ans[0]=1;a[1]=1;
    while(n)
    {
        if(n&1){polymul(ans,a,ans,k,k); polymod(ans);}
        polymul(a,a,a,k,k); polymod(a);
        n>>=1;
    }
    for(int i=0;i<k;i++) qvq=(qvq+ans[i]*st[i])%p;
    cout<<qvq; 
    return 0;
}