题意:
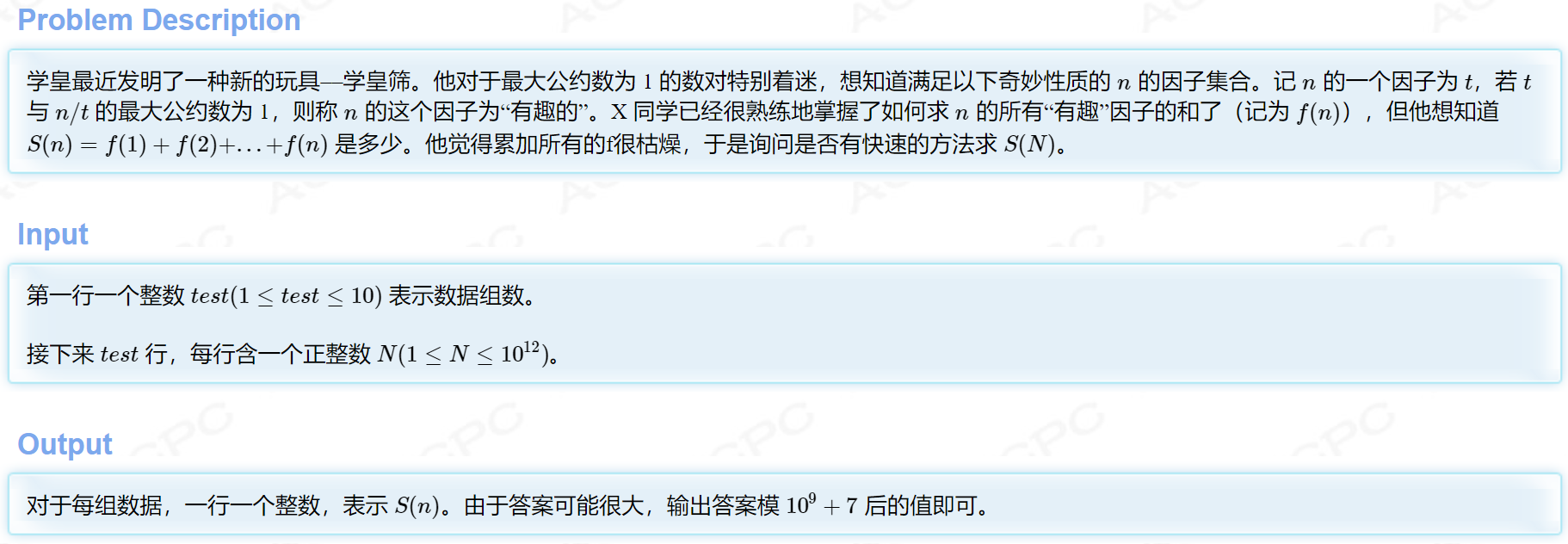
分析:
题目要求的是:
[sum_{i=1}^{n}{sum_{t|i}{t[gcd(t,frac{i}{t})==1]}}
]
推导:
[egin{align}
S(n) &= sum_{i=1}^{n}{sum_{t|i}{t[gcd(t,frac{i}{t})==1]}}\
& = sum_{i=1}^{n}{sum_{t|i}{tsum_{d|(t,frac{i}{t})}{mu(d)}}}\
& = sum_{d=1}^{n}{mu(d)sum_{t=1}^{lfloor n/d
floor}{tdsum_{i=1}^{lfloor n/dt^2
floor}{1}}}
end{align}
]
令 (T=d^2t),
[egin{align}
S(n) &= sum_{T=1}^{n}{left(sum_{i=1}^{lfloor n/T
floor}{1}
ight)sum_{d^2|T}{mu(d)lfloor frac{T}{d}
floor}}\
& = sum_{T=1}^{n}{lfloor frac{n}{T}
floor sum_{d^2|T}{mu(d)lfloor frac{T}{d}
floor}}\
& = sum_{d=1}^{sqrt{n}}{mu(d)dsum_{T=1}^{lfloor n/d^2
floor}{lfloor frac{n/d^2}{T}
floor T}}
end{align}
]
令 (G(k)=sum_{i=1}^{k}{lfloor frac{k}{i} floor i}),
[egin{align}
S(n) &= sum_{d=1}^{sqrt{n}}{mu(d)d}G(lfloor frac{n}{d^2}
floor)
end{align}
]
实现时,(G(k)) 和 最终公式的计算均可以借助分块,复杂度:(O(sqrt{n}logn))。
代码:
实现说明:
1.在预处理 (1e6) 以内的 (G(k)) 时,采用了枚举因子的处理方式,很巧妙,大于 (1e6) 时采用直接分块的方式;
2.不能直接对 (S(n)) 进行分块,故使用代码中的方式确定区间的右端点;
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const int N=1e6+6;
int mu[N];
int prime[N],cnt;
bool vis[N];
ll g[N],sum[N],inv2=500000004;
ll getsum(ll x)
{
ll res=0;
x%=mod;
res=(1+x)*x%mod*inv2%mod;
return res;
}
void init()
{
int maxn=1e6;
mu[1]=1;
cnt=0;
memset(vis,false,sizeof(vis));
for(int i=2;i<=maxn;i++)
{
if(!vis[i])
{
prime[++cnt]=i;
mu[i]=-1;
}
for(int j=1;j<=cnt&&prime[j]*i<=maxn;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0)
{
mu[i*prime[j]]=0;
break;
}
else
mu[i*prime[j]]=-mu[i];
}
}
for(int d=1;d<=maxn;d++)//1e6以内G(k)
{
for(int i=d;i<=maxn;i+=d)
g[i]=(g[i]+d)%mod;
}
sum[0]=0;
for(int i=1;i<=maxn;i++)
{
sum[i]=(sum[i-1]+1LL*mu[i]*i+mod)%mod;//i*mu[i]的前缀和
g[i]=(g[i]+g[i-1])%mod;//G(k)
}
}
ll solve(ll k)
{
if(k<=1e6) return g[k];
ll res=0;
for(ll l=1,r;l<=k;l=r+1)
{
r=min(k,k/(k/l));
res=(res+(k/l)*(getsum(1LL*r)-getsum(1LL*(l-1)))%mod+mod)%mod;
}
return res;
}
int main()
{
int test;
init();
scanf("%d",&test);
while(test--)
{
ll n,ans=0;
scanf("%lld",&n);
ll m=floor(sqrt(1.0*n));
for(ll l=1,r;l<=m;l=r+1)//好像不能直接用分块写
{
ll t=1LL*l*l;
ll x=n/t;
r=l;
while(n/(1LL*r*r)==x) r++;
r--;
ans=(ans+(sum[r]-sum[l-1])*solve(x)%mod+mod)%mod;
}
printf("%lld
",ans);
}
return 0;
}
参考博客:https://blog.csdn.net/weixin_44282912/article/details/107454309