题意:
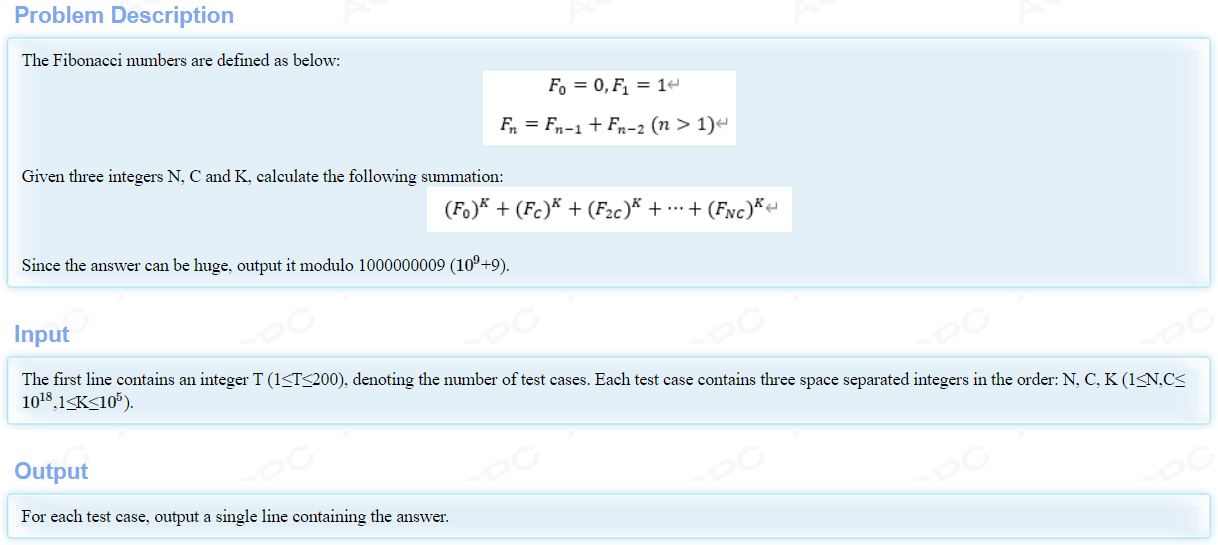
分析:
一开始想的是用矩阵来求,但发现样例一直过不去。最后才发现,((AB)^k
e A^kB^k),其中 (A,B) 为矩阵,做了怎么久才发现是一个假算法。
看来题解才发现用的是斐波那契数列的通项公式:
[F_n=frac{1}{sqrt{5}}[(frac{1+sqrt{5}}{2})^n-(frac{1-sqrt{5}}{2})^n]
]
同时还要知道:(5) 是 (1e9+9) 的二次剩余
且有:
[383008016^2 equiv 616991993^2 equiv 5 (mod 1e9+9)
]
由此可知,在模 (1e9+9) 的情况下,(sqrt{5}) 与 (383008016) 同余。
可以求出 (sqrt{5}) 的逆元为 (invsqrt5=276601605)。
令 (a=frac{1+sqrt{5}}{2},b=frac{1-sqrt{5}}{2}),通过快速幂可以求得:(a=691504013,b=308495997)。
所以,有:
[F_{n}^{k}=invsqrt5^k*[a^n-b^n]^k
]
而根据二项式展开,有:
[(a^n-b^n)^k=C(k,0)*(a^n)^0*(b^n)^k+C(k,1)*(a^n)^{1}*(b^n)^{k-1}+...+C(k,k)*(a^n)^k*(b^n)^0
]
所以,
[ans=invsqrt5^k*sum_{i=1}^{k}{[C(k,i)sum_{j=1}^{n}{(a^{jc})^i(-b^{jc})^{k-i}}]}
]
又根据等比数列的求和公式:
[S_i=sum_{j=1}^{n}{(a^{jc})^i(-b^{jc})^{k-i}}=frac{1-(a^{cin}*b^{c(k-i)n})}{1-a^{ci}*b^{c(k-i)}}*a^{ci}*(-1)^{k-i}*b^{c(k-i)}
]
注意特判公比为 (1) 的情况,其中(a^{cin},b^{c(k-i)n},a^{jc},b^{jc}) 均可以预处理出来。
最终的答案为:
[ans=invsqrt5^k*sum_{i=1}^{k}{S_i}
]
复杂度为:(O(klogn)),能预处理的都预处理,否则容易超时。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
const int mod=1e9+9;
const int phi=1e9+8;
ll C[N],fac[N],inv[N],sa[N],sb[N];
ll inv2=500000005,p=383008016,q=276601605;
ll power(ll a,ll b)
{
ll res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
void init()//预处理出阶乘和阶乘逆元
{
int maxn=1e5;
fac[0]=1;
for(int i=1;i<=maxn;i++)
fac[i]=fac[i-1]*i%mod;
inv[maxn]=power(fac[maxn],mod-2);
for(int i=maxn-1;i>=0;i--)
inv[i]=inv[i+1]*(i+1)%mod;
}
void getC(ll k)
{
for(int i=0;i<=k;i++)
C[i]=fac[k]*inv[i]%mod*inv[k-i]%mod;
}
int main()
{
int t;
init();
scanf("%d",&t);
//fn=q*(x^n-y^n)
ll x=(1+p)*inv2%mod;
ll y=(1-p+mod)*inv2%mod;
while(t--)
{
ll n,c,k,ans=0;
scanf("%lld%lld%lld",&n,&c,&k);
getC(k);//预处理组合数
ll tx=power(x,c);
ll ty=power(y,c);
ll invty=power(ty,mod-2);
sa[0]=power(ty,k);
for(int i=1;i<=k;i++)
sa[i]=sa[i-1]*tx%mod*invty%mod;
tx=power(tx,n);
ty=power(ty,n);
invty=power(ty,mod-2);
sb[0]=power(ty,k);
for(int i=1;i<=k;i++)
sb[i]=sb[i-1]*tx%mod*invty%mod;
int f=((k%2)?1:-1);
for(int i=0;i<=k;i++)
{
f=-f;
if(sa[i]==1)
{
ll tmp=C[i]*f*(n%mod)%mod;
ans=(ans+tmp+mod)%mod;
continue;
}
ll up=(1-sb[i]+mod)%mod;
ll down=(1-sa[i]+mod)%mod;
down=power(down,mod-2);
ll tmp=up*down%mod;
tmp=(tmp*sa[i]%mod*f+mod)%mod;
tmp=tmp*C[i]%mod;
ans=(ans+tmp)%mod;
}
ans=ans*power(q,k)%mod;
printf("%lld
",ans);
}
return 0;
}