学有向图的连通性不可不学的一个东西就是强连通分量——tarjan算法。
例题
题目描述
给你一张有n个节点,m条边的有向图,求其强连通分量的个数(如果该强连通分量只有一个点则不算在其中)。
输入格式
第1行,两个整数n和m。(n <= 10000,m <= 50000)
第2到(m + 1)行,每行两个整数u和v表示有一条u -> v的边。
输出格式
强连通分量的个数(如果该强连通分量只有一个点则不算在其中)。
输入输出样例
输入
5 4
2 4
3 5
1 2
4 1
输出
1
强连通分量——tarjan算法
再说强连通分量SCC之前你先得了解两个概念:强连通图,其实很好理解,就是这张图中任意两点都可以互相到达(直接或间接);强连通子图,也很好理解,就是一张图中的子图,而这个子图是一个强连通图。那么强连通分量其实就是一张图一个强连通子图,且没有其他能包含这张子图的强连通子图,则称其为一个强连通分量。举个例子,如下图。
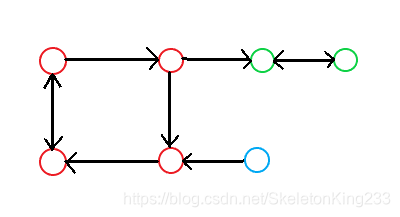
而tarjan算法其实就是把这张图当成一个多叉树,我们任选一个点为根节点,之后按dfs序跑这个树去找环,这里我们要将边分为三类:
- 树边:在树上的边。
- 返祖边:返回到祖先的边。
- 枝杈边:连接两个子树的边,其实没什么用。
其实找强连通分量就是在找环,也就是再找返祖边,那么如何判断一个点到下一个点的边是什么边呢?这个很简单,我们先要维护一个数组dfn[i]表示i节点在树上的dfs序数,这样每次如果说dfn[y] == 0即尚未到过下一个点,那么这一定是一条树边。
接下来我们来判断返祖边和枝杈边,我们可以用一个栈来记录,每到一个点就将该点push到栈中,每找到一个强连通分量就pop掉(后面会详细解释),之后再来一个数组ins[i]表示当前i节点是否在栈中,每次push就将对应点设为true,每次pop就将对应点设为false。这样如果下一个点dfn[y] == 0且ins[i] == true则该边为返祖边,否则为枝杈边。
会判断边了,我们就可以真正开始学习tarjan算法了。这里我们还要维护一个数组low[i]表示i节点及其子节点能直接或间接到达的dfs序数最小的点,这个数组的初值就是i节点自己的dfs序数,之后每次选一条与之相连的边判断:如果这是树边就再去跑其子节点,然后选自己的low和子节点low的最小值为自己的low;如果是返祖边直接选自己的low和返祖点dfs序的最小值为自己的low;如果是枝杈边直接跳过。
这样我们就可以发现如果最后跑完了当前点的所有边,low[x]还等于自己的dfs序数,也就代表这个点跑了一圈还只能到自己的点,那么以这个点为根节点的树上的所有点组成了一个强连通分量。
接下来给这个树上的所有点进行染色,这里我们又可以用到栈了,一边不停地pop,一边取top并将其的颜色染为一个color[0],顺便用cnt数组计个数(cnt[i]表示颜色为i的点的数目),直到当前栈的top等于当前点x了,就停止。
简而言之,其实tarjan算法就是去找返祖边,之后染色计数。这里要注意一下此题的答案是不包含只有一个点的强连通分量的,即cnt[i] > 1时才让ans++。
最后,算一下算法时间复杂度:我们发现需要便利所有边和点一次,所以总时间复杂度大概为O(n + m)级别的。
代码
# include <cstdio>
# include <algorithm>
# include <cmath>
# include <cstring>
# include <vector>
# include <stack>
using namespace std;
const int N_MAX = 10000, M_MAX = 50000;
int n, m;
vector <int> g[N_MAX + 10];
int now, dfn[N_MAX + 10], low[N_MAX + 10];
bool ins[N_MAX + 10];
stack <int> s;
int color[N_MAX + 10], cnt[N_MAX + 10];
void addEdge(int x, int y)
{
g[x].push_back(y);
}
void tarjan(int x)
{
dfn[x] = low[x] = ++now;
ins[x] = true;
s.push(x);
for (int i = 0; i < (int) g[x].size(); i++) {
int y = g[x][i];
if (dfn[y] == 0) tarjan(y), low[x] = min(low[x], low[y]);
else if (ins[y]) low[x] = min(low[x], dfn[y]);
}
if (low[x] != dfn[x]) return;
color[x] = ++color[0];
cnt[color[0]]++;
while (s.top() != x) {
int y = s.top();
color[y] = color[0];
ins[y] = false;
s.pop();
cnt[color[0]]++;
}
ins[x] = false;
s.pop();
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int x, y;
scanf("%d%d", &x, &y);
addEdge(x, y);
}
for (int i = 1; i <= n; i++)
if (dfn[i] == 0) tarjan(i);
int ans = 0;
for (int i = 1; i <= color[0]; i++)
if (cnt[i] > 1) ans++;
printf("%d
", ans);
return 0;
}