9.3 欧拉定理 && 欧拉降幂 （扩展欧拉定理）&& 指数循环节

上周六南京邀请赛b题求幂塔函数 ,没做出来 ...

幂塔函数的关键就是说 a^m %mod 其中m特别大时的求法，会求这个直接递归求解就可以解决幂塔函数

当时打表发现了指数循环节（所以说以后要好好训练 打表 这种技能 ，虽然打cf时用不到 ，但比赛时经常会用到）这种东西，想到应该有确定循环节长度的算法

后来队友想到了有欧拉降幂这种东西 ，欧拉降幂就是说，指数循环节的长度就是模数的欧拉函数值

但奈何数论不好，当时不理解欧拉降幂的原理 ，所以执着于公式本身的形式（其实关于底数a与模数m不同情况下的讨论就是为了表达 指数循环节的长度就是模数的欧拉函数值 这一个东西），最后也没有写出来

其实熟悉数论的思考方式的话应该能自然联想到指数循环节的长度与欧拉函数有关的，可惜本人对此种思考方式一窍不通（正在努力适应中）

下面记一下欧拉降幂 ，同其他数论结论一样， 其证明也是运用构造思想.

数论概念：

1. 完全剩余系

在模n的剩余类中各取一个元素，则这n个数就构成了模n的一个完全剩余系。

取最小非负整数的完全剩余系就是${0 ，1 ，2 ... ，n-1}$;

2.简化剩余系

将任一个模m的完全剩余系中φ(m)个与m互质的数取出，则构成一个模m的简化剩余系

了解上述概念后就能理解欧拉定理：

欧拉降幂（扩展欧拉定理）的证明比较复杂，详见：https://blog.csdn.net/synapse7/article/details/19610361

就是说 ：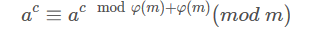

虽然不知道欧拉降幂的发明者是谁， 但我猜想他是先发现指数循环节的长度为 phi（m）,然后再根据结论构造证明欧拉降幂的

所以说打表真的很重要（嗯）

求幂塔函数中的另一个优化剪枝是当递归出现模数等于1时直接返回0 ，这个剪枝也很重要

补： 补题过程中发现要加一个mod（）函数

ll mo( ll a ,ll m ){
    if( a <= m )return a;
    return a%m + m;
}

原因：

1.不判断a与m的关系直接返回 a%m + m ，则a%phi+phi可能会超过题目范围导致错误
2.当a==m时不能返回0，要返回m，因为循环节的第一个是a^1而不是a^0

幂塔函数代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <set>
#include <queue>
#include <stack>
#include <string>
#include <cstring>
#include <vector>
#define mem( a ,x ) memset( a , x ,sizeof(a) )
#define rep( i ,x ,y ) for( int i = x ; i<=y ;i++ )
#define lson  l ,mid ,pos>>1
#define rson mid+1 ,r ,pos>>1|1

using namespace std;
typedef long long ll ;
typedef pair<int ,int> pii;
typedef pair<ll ,int> pli;
const int inf = 0x3f3f3f3f;
const int N = 1e6+5;

int cnt = 0;
ll phi[N+5] ,unprime[N+5] ,prime[N+5];

void getphi( ){
     unprime[1]= 1;
     phi[1] = 1;
     for( ll i = 2 ; i<= N ;i++ ){
         if( !unprime[i] )prime[++cnt] = i , phi[i] = i-1;
         for( ll j = 1; j<= cnt && i*prime[j] <= N ;j++ ){
             unprime[ i*prime[j] ] = 1;
             phi[ i*prime[j] ] = phi[ i ] * phi[ prime[j] ];
             if( i % prime[j] == 0 ){
                 phi[ i*prime[j] ] = phi[ i ] *( 1ll + phi[ prime[j] ] );
                 break;
                }
            }
     }
}

ll mo( ll a ,ll m ){
    if( a <= m )return a;
    return a%m + m;
}

ll q_pow( ll x ,ll p ,ll m ){
     ll ans = 1;
     while( p ){
         if( p & 1 )ans = mo( ans*x ,m );
         x = mo( x*x , m );
         p >>= 1;
     }
     return mo( ans , m);
}


ll solve(ll a, ll p ,ll m ){
     if( m==1 )return mo( a ,1 );
     if( p == 1 )return mo( a ,m );
     return q_pow( a , solve( a , p-1 , phi[m] ) , m);
}
int main( ){
     int t;
     ll a ,b ,m;
     getphi( );
     scanf( "%d" ,&t );
     while( t-- ){
         scanf( "%lld%lld%lld" ,&a ,&b ,&m );
         if( b==0 )printf("%lld
" ,1%m );
         else printf( "%lld
" ,solve( a ,b ,m )%m );
     }
     return 0;
}